Відношення еквівалентності

Відношення R називається відношенням еквівалентності, якщо воно має такі властивості:

а) рефлективності: (x, х) Î R при будь-якому х Î Х;

б) симетричності: з (x ₁, х ₂) Î R випливає (x ₂, х ₁) Î R;

в) транзитивності: якщо (x ₁, х ₂) Î R і (x ₂, х ₃) Î R, то (x ₁, х ₃) Î R;

Замість того, щоб писати (x ₁, х ₂) Î R, часто пишуть x ₁ ~ x ₂ або x ₁ º x ₂(mod R) (читається так: x ₁ конгруентно x ₂ за модулем R) чи, простіше, (x ₁ ~ x ₂ або x ₁ º x ₂, якщо немає необхідності ще раз вказувати, що мова йде про одне й те саме відношення R).

Приклади: 1)°Визначимо на множині цілих чисел Z відношення еквівалентності так, що р º q, тоді і тільки тоді, коли p - q ділиться без остачі на деяке наперед задане натуральне число m >1, скажімо m =5. У теорії чисел таке відношення записується у вигляді р º q (mod т).

2)°Нехай Х - множина прямих на площині. Визначимо відношення еквівалентності для прямих x ₁ і x _2, покладаючи x ₁ º x ₂, коли ці прямі паралельні.

3) Нехай Х – множина всіх студентів, які присутні на лекції з дискретної математики. Два студенти еквівалентні, якщо вони народилися в тому самому місяці року.

Для x Î X позначимо через K (x)підмножину, що складається з елементів, еквівалентних x, тобто K (x) = { y | y Î X; y ~ x }. Таку підмножину будемо називати класом еквівалентності. Зрозуміло, що клас еквівалентності є множиною всіх елементів, еквівалентних довільному елементу з цього класу. Справедлива наступна теорема:

Теорема 1. Два класи еквівалентності або не перетинаються або співпадають.

Доведення. Припустимо, що перетин множин K (x)і K (х')непорожній, і візьмемо z Î K (x) Ç K (х'). Клас еквівалентності K (x) утворений з елементів, еквівалентних одному зі своїх елементів x. Оскільки x і z еквівалентні, то за властивістю транзитивності отримуємо, що K (x) утворений також з елементів, еквівалентних z. Аналогічно K (х') утворений з елементів, еквівалентних z. Таким чином, K (х) і K (х') співпадають.

Відношення еквівалентності на множині Х породжує деяке розбиття множини Х, тобто деяку сім’ю непорожніх підмножин множини X (класів еквівалентності), які попарно не перетинаються,а їхоб’єднання рівне X. Будь-які два елементи з одного класу зв’язані відношенням еквівалентності, тобто еквівалентні;з різних класів - не еквівалентні.

Навпаки, будь-яке розбиття множини X: Х = 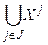, де X_j непорожні і попарно не перетинаються, визначає деяке відношення еквівалентності, а саме x º х', якщо існує такий індекс j Î J, що x, х' Î X_j. У цьому випадку підмножини X_j є класами еквівалентності для цього відношення.

Фактор-множина

Виходячи із сказаного кожен клас еквівалентності X_j є підмножиною множини X, що складається з елементів, еквівалентних деякому фіксованому елементу цієї множини. Тому можна розглянути і множину всіх класів еквівалентності, яку звичайно називають фактор-множиною за даним відношенням еквівалентності R і позначають наступним чином Х / R. Якщо через K (x) позначити клас еквівалентності елемента x, то K (x) є елементом фактор-множини та x Î K (x).

Можна дати просту інтерпретацію фактор-множини на прикладах відношень еквівалентності, наведених раніше (1, 2, 3, 4, 5):

1)°фактор- множина - це множина Z_m цілих чисел, порівняних за модулем m;

2)°фактор- множина - це множина напрямлених прямих на площині;

3)°фактор- множина - це множина місяців року. Вона може мати менше 12 місяців, бо в аудиторії може не виявитися студентів, які народилися в одному з місяців, скажімо в лютому.

 

Рівнопотужні множини

Розглянемо відображення з множини натуральних чисел N в множину парних натуральних чисел N ₂, яке кожному натуральному числу ставить у відповідність подвоєне число, тобто бієктивне відображення f (п) = 2 п. Тоді можна сказати, що існує стільки парних натуральних чисел, скільки й натуральних, а також, що y випадку нескінченних множин може існувати бієктивне відображення деякої множини на її підмножину, яка відмінна від самої множини. Завдяки поняттю бієктивного відображення можна порівнювати між собою нескінченні множини.

Дві множини X та Y називаються рівнопотужними, якщо існує принаймні одне бієктивне відображення f : X → Y.

Відношення ” X рівнопотужна Y “ є відношенням еквівалентності між множинами. Клас еквівалентності, тобто клас всіх множин рівнопотужних даній множині, називається потужністю або кардинальним числом. Скінченні кардинальні числа – це класи еквівалентності скінченних множин. Ці числа за визначенням є натуральними числами 0, 1, 2,.... Слід відзначити, що ми приймаємо як первинне поняття натуральні числа, але їх строге математичне визначення досить складне. Як наслідок не легко apriori означити скінченні множини. Часто за визначенням вважають множину скінченною, якщо вона не рівнопотужна ніякій зі своїх підмножин, відмінних від самої множини, а потім доводять, що кардинальне число має властивості натуральних чисел.

Перейдемо до двох найбільш важливих нескінченних потужностей: потужності зчислених множин і потужності континууму.

 

Зчисленні множини

Множина називається зчисленною, якщо вона рівнопотужна множині натуральних чисел N. Множина зчисленна, якщо існує хоча б одна бієкція цієї множини в множину N. Іншими словами, множина зчисленна, якщо її елементи можна пронумерувати натуральними числами і номери не будуть повторюватися.

Раніше ми з’ясували, що множина парних натуральних чисел N ₂ є зчисленною.

Задамо відображення f: Z → N так: f (z)=2 z при z >0, f (z)=2| z |+1 при z ≤0. Воно бієктивне і, значить, множина цілих чисел Z також є зчисленною.

Покажемо, що множина N ´ N рівнопотужна множині N. Дійсно, з наведеної далі схеми

 

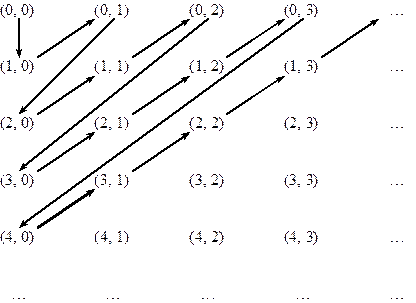
бачимо, що відображення 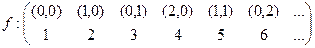, тобто f: N ´ N → N є бієкцією.

Інший варіант бієктивного відображення f: N ´ N → N наведено далі.

 

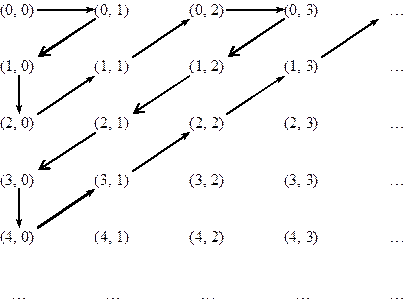
Покажемо, що множина Z ´ Z рівнопотужна множині N. Далі наведено схему, яка задає відповідне бієктивне відображення f: Z ´ Z → N

 

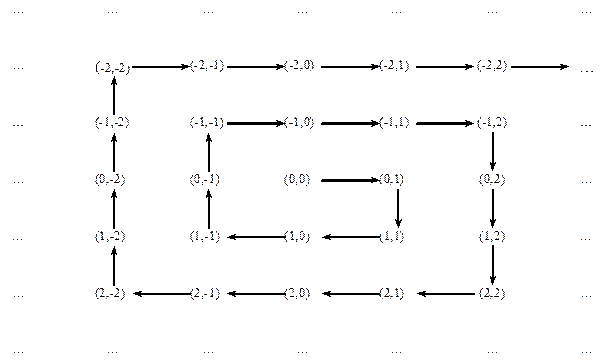
Таким чином, множина Z ´ Z також є зчисленною.

Покажемо, що й множина раціональних чисел зчисленна. Множину раціональних чисел можна розглядати так: Q = {(m, n) | m − ціле число, n − натуральне число, найбільший спільний дільник m та n дорівнює 1}.

На наведеній далі схемі зображено впорядковані пари - елементи множини Q ₁ = {(m, n) | m − ціле число, n − натуральне число}. Оскільки різні такі пари можуть задавати одне і те ж раціональне число (наприклад, пари (1,2), (2,4), (3,6) і т.д. задають число ½), то кожен елемент множини Q на схемі зображаємо променем, початком якого є пара (m, n), у цьому разі найбільший спільний дільник m та n дорівнює 1. Починаючи з неї і через всі подальші пари, що задають те саме раціональне число, проводимо промінь – по суті об’єднуємо такі пари в одну групу.

Нумеруємо елементи множини Q прямими зі стрілками, що послідовно з’єднують початки променів. Загальний шлях нумерації складається з низки умовних півкіл. У кожному півколі прямі зі стрілками з’єднують ті пари, що мають рівні суми | m | + | n |.

Усі розглянуті досі множини виявилися зчисленними множинами. Виникає запитання: а чи існують нескінченні множини, які не є зчисленними? Відповідь отримаємо далі.

Потужність континууму

Теорема 2 (Кантора). Множина дійсних чисел з інтервалу (0, 1) не є зчисленною.

Дійсно, доведемо, що множина X = (0, 1) дійсних чисел, які задовольняють нерівність 0 ≤ x ≤ 1, не є зчисленною.

Доведення проведемо від протилежного. Припустимо, що X зчисленна й існує деяка бієкція N на Х, тобто елементи X можуть бути записані y вигляді деякої послідовності x ₁, x ₂, x ₃, …, елементи якої попарно різні. Крім того, розглянемо дійсне число ξ, яке визначимо так: перед комою поставимо 0, потім як j -й десятковий знак виберемо довільне ціле число між 1 і 8, яке відрізняється від j -го десяткового знака числа х_j. Таким способом ми утворюємо нескінченний дріб, що визначає деяке число ξ. Для довільного натурального j маємо таке. Оскільки j -й десятковий знак числа ξ відрізняється від j -го десяткового знака числа х_j і всі десяткові знаки числа ξ відрізняються від 0 і 9, то ξ ≠ х_j (не допускаємо знаків 0 і 9, бо 0,102000... і 0,101999... одне і те ж саме число). Значить число ξ не збігається ні з одним з чисел послідовності x ₁, x ₂, x ₃, … Ми отримали суперечність. Це й доводить теорему.

Будемо потужність множини X = (0, 1) називати потужністю континууму. Потужність континууму - це також потужність множини всіх дійсних чисел, оскільки 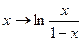є бієкцією (0, 1) на R.

Дійсно, нехай x1≠x2 Припустимо, що 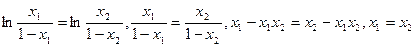суперечність Отже, це відображення ін’єктивне.

Це відображення також є сюр’єктивним, бо з рівності .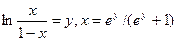

Наведемо без доведення теорему.

Теорема 3 (Бернштейна). Нехай X та Y – дві довільні множини. Тоді 1) або існує ін’єкція X в Y, або існує ін’єкція Y в X (обидві обставини не виключають одна одну); 2) якщо існує одночасно ін’єкція X в Y та ін’єкція Y в X, то існує також бієкція X на Y.

Наслідок. Для заданих множин X та Y є тільки три можливості:

а) існує ін’єкція X в Y і не існує ін’єкція Y в X. В цьому випадку говорять, що Y має потужність строго більшу потужності X, або що X має потужність, строго меншу потужності Y;

б) існує ін’єкція Y в X і не існує ін’єкція X в Y. Тоді X має потужність строго більшу потужності Y або Y має потужність, строго меншу потужності X;

в) існує бієкція X в Y. У цьому випадку кажуть, що X і Y мають однакову потужність або рівнопотужні.

Теорема 4. Якою б не була множина X, множина її підмножин має потужність, строго більшу потужності X.

Виходячи з останньої теореми, для нескінченних множин існує нескінченне число класів рівнопотужних множин.

На завершення сформулюємо континуум-гіпотезу. Згідно цієї гіпотези, клас множини P (N) іде одразу за класом множини N (тобто між ними не можна вставити проміжний клас). Узагальнена континуум-гіпотеза полягає в припущенні, що при довільній множині X клас множини P (X) іде безпосередньо за класом множини X. Доведено (П. Коен, 1968 р.), що континуум-гіпотеза не має рішення – її не можливо ані довести, ані спростувати, можна тільки прийняти її або протилежне їй твердження як аксіому.