Основні поняття і операції

Визначення графу

Предметом перших задач теорії графів були конфігурації, які складаються з точок і ліній, які їх з’єднують. При цьому несуттєво, прямі ці лінії або вони є криволінійними дугами. Важливо лише те, що вони з’єднують дані точки.

Визначення. Розглянемо множину V, яка складається з точок, частина яких з’єднана між собою. Назвемо V множиною вершин, а об’єкт v Î V - вершиною. Граф

G = G (V)

з множиною вершин V - це деяка сукупність пар вигляду

e = (a, b),

де a, b Î V вказують, які пари вершин з’єднані між собою. Відповідно до геометричних уявлень про граф кожна така пара (a, b) називається ребром графу, а „ а ” і „ b ” – кінцями ребра. З іншого боку, оскільки

e = (a, b) Î V ´ V,

то граф

G (V) Í V ´ V.

Визначення. Якщо у визначенні ребра графу не брати до уваги послідовність його кінців, тобто вважати, що

e = (a, b) = (b, a),

то говорять, що e – неорієнтоване ребро. В протилежному випадку e = (a, b) - орієнтоване ребро, в якому „ а ” – початкова вершина, а „ b ” – кінцева.

Визначення. Якщо e = (a, b), то говорять, що ребро e інцидентне вершинам „ а ” і „ b ”, а вершини „ а ” і „ b ” інцидентні ребру e.

 

Зображення графів

Визначення. Граф G називається неорієнтованим, якщо кожне його ребро є неорієнтованим. Граф G називається орієнтованим, якщо кожне його ребро є орієнтованим.

 

 

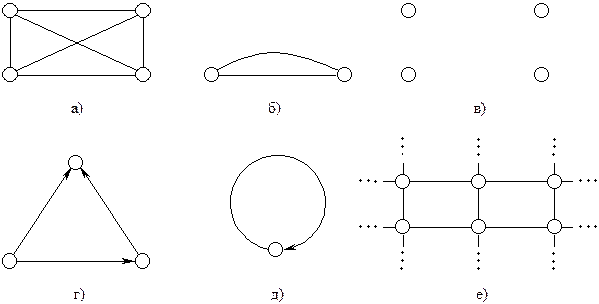
Рис. 1.

 

На рис. 1.а, б, в, е зображені деякі неорієнтовані графи, а на рис. 1.г, д – деякі орієнтовані графи (напрями ребер зображені стрілками). Лінії, які відповідають ребрам графів, можуть перетинатись на рисунку, але точки їх перетину не обов’язково повинні бути вершинами графу (див.рис.1.а).

Якщо два ребра інцидентні одній парі вершин, то такі ребра називаються кратними (див.рис.1.б). Ребро, яке з’єднує вершину саму з собою, називають петлею (див.рис.1.д).

Визначення. Граф називається скінченним, якщо кількість ребер в ньому є скінченною (рис.1.а, б, г); інакше граф називають нескінченним (рис.1.е).

Визначення. Вершина графу, не інцидентна жодному ребру, називається ізольованою. Якщо граф складається тільки з ізольованих вершин, то він називається нульграфом (рис.1.в).

Визначення. Будемо говорити, що два графи G і G ’ є ізоморфними, якщо існує така відповідність між множинами їх вершин V і V ’, що у графі G вершини з’єднані між собою тоді і тільки тоді, коли з’єднані між собою відповідні їм вершини у графі G ’. Якщо ребра орієнтовані, то їх напрямки повинні відповідати один одному.

Наприклад:

 

 

Твердження. Ізоморфні графи мають однакові властивості.

Відповідно з даними твердженнями ізоморфні графи надалі будемо ототожнювати.

 

 

Способи задання графів

Графічний опис графів є незручним для їх аналізу на ЕОМ. Тому розглянемо табличні способи задання графів.

Надалі будемо розглядати тільки скінченні графи, у яких множини вершин V = { v ₁, …, v_n } і ребер E = { e ₁, …, e_m } є скінченними.

Визначення. Матриця суміжності вершин графу G (V) (позначається M (G) = { M_ij }) - це квадратна матриця розміру n ´ n, в якій M_ij - кількість ребер, які з’єднують V_i з V_j в графі G. Якщо граф G неорієнтований, то

M_ij = M_ji,

тобто матриця М є симетричною.

На рис.2 зображений деякий неорієнтований граф; відповідна матриця суміжності вершин приведена в табл.1.

 

Рис.2	Таблиця 1

 

Граф також може бути описаний за допомогою матриці інцидентності (позначається N (G) = { N_ij }), яка має n рядків (вершини) і m стовпців (ребра). Для неорієнтованого графу N_ij = 1, якщо вершина v_i інцидентна ребру e_j; в протилежному випадку - N_ij = 0.

Для орієнтованого графу N_ij = 1, якщо v_i - початкова вершина ребра e_j; N_ij = ‑1, якщо v_i - кінцева вершина ребра e_j; N_ij = 0, якщо вершина v_i не інцидентна ребру e_j.

У табл. 2 наведена матриця інцидентності для неорієнтованого графу, зображеного на рис. 2.

На рис. 3 зображений орієнтований граф, матриця інцидентності для якого наведена в табл. 3.

Неорієнтований граф без петель G може бути також описаний квадратною матрицею суміжності ребер (позначається I (G) = { I_ij }) розміром m ´ m, причому I_ij = 1, якщо i ¹ j і у ребер e_i і e_j є спільна вершина. В протилежному випаду - I_ij = 0.

Для графу, зображеного на рис. 2, відповідна матриця суміжності ребер приведена в табл. 4.

 

Таблиця 2

	І	ІІ	ІІІ	IV	V	VI	VII	VIII	IX

 

 

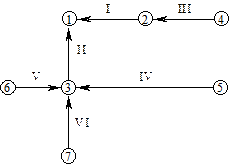Рис. 3	Таблиця 3
	І	ІІ	ІІІ	IV	V	VI
	-1	-1
			-1
				-1	-1	-1

 

 

Таблиця 4

	І	ІІ	ІІІ	IV	V	VI	VII	VIII	IX
І
ІІ
ІІІ
IV
V
VI
VII
VIII
IX

 

Степінь вершини графа

 

Нехай G (V) - неорієнтований граф.

Визначення. Степенем r (a) деякої вершини a Î V називається кількість ребер графу, інцидентних цій вершині.

Якщо граф заданий матрицею суміжності вершин, то

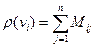(1)

Для матриці інцидентності аналогічна формула має вигляд

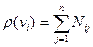(2)

Число ребер у графі G позначимо через v_E = v_E (G). При підрахунку суми 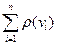кожне ребро e (v_i, v_j), графу G підраховується двічі: один раз – як таке, що з’єднує вершину v_i з v_j, а другий раз – як таке, що з’єднує v_j з v_i. Тому

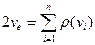(3)

(формула (3) залишається правильною і для графу з петлями, якщо їх розглядати як подвійні ребра).

Оскільки в лівій частині формули (3) стоїть парне число, то це означає, що у скінченному графі без петель кількість вершин з непарним степенем – парна.

Визначення. Граф називається однорідним степеня k, якщо r (v_i = k), для всіх v_i Î V.

В однорідному графі кількість ребер згідно з формулою (3) v_E = nk /2.

Визначення. Повний граф U = U (V) - це неорієнтований граф, у якому дві довільні вершини з’єднані рівно одним ребром.

Зрозуміло, що повний граф U (V) з n вершинами – це однорідний граф степеня (n ‑ 1). Тому v_E = n (n – 1) / 2.

Визначення. Повний граф з петлями U ₀ = U ₀(V) - це повний граф, у якому до кожної вершини додана петля.

Кількість ребер у повному графі з петлями v_E (U ₀) = v_E (U) + n = n (n + 1) / 2.

Нехай тепер G (V) - орієнтований граф. Тоді через r (v_i) і r* (v_i) позначають кількість ребер, які виходять з вершини v_i і входять в вершину v_i відповідно.

Аналогічно попередньому кількість ребер в орієнтованому графі

.
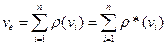