Примеры решения задач по волновой оптике

Пример 1. На зеркала Френеля, угол между которыми a = 10', падает монохромати­ческий свет от узкой щели S, находящейся на расстоянии r = 0,1 м от линии их пересечения Отраженный от зеркал свет дает интерференционную кар­тину на экране Э, отстоящем на расcтоянии а = 2,7 м от линии их пересечения, причем расстояние между интерференционными полосами равно х = 2,9 · 10^{-11 м} . Определить длину волны λ света.

2a

a K

S

S 1

S 2

d

r

a

l

Э

L

 

Решение

После отражения от зеркал OK, OL световые волны распространяются так, будто вышли из двух когерентных источников S₁ и S₂, являющихся мнимыми изображениями щели S. Пусть расстояние между источниками S₁ и S₂, равно d, а расстояние от них до экрана l. Величины l, d, x, l связаны соотно­шением

λ = xd/l. (1)

Чтобы найти d и l, учтем, что точки S₁ и S₂ симметричны точке S относительно соответствующих зеркал. Поэтому S₁O = S₂O = r и ÐS₁OS₂ = 2α. Так как угол α весьма мал и экран обычно распо­лагается параллельно отрезку S₁S₂, то можно записать:

d = 2ar, l = r + а.

Подставив эти значения d,l в формулу (1), получим

λ = 2arx/(r + а).

После подстановки числовых значений величин (предварительно выразив угол α в радианах) найдем

l = 6 × 10^{-7 м = 0,6 мкм.}

Пример 2. Для уменьшения потерь света при отражении от стекла на поверхность объектива (n₂ = 1,7) нанесена тонкая прозрачная пленка (n = 1,3). При какой на­именьшей толщине ее произойдет максимальное ослаб­ление отраженного света, длина волны которого при­ходится на среднюю часть видимого спектра (λ₀ = 0,56 мкм)? Считать, что лучи падают нормально к поверхности объектива.

Решение

Свет, падая на объектив, отражается как от перед­ней, так и от задней поверхностей тонкой пленки. Отраженные лучи интерферируют. Условие минимума интенсивности света при интерференции выражается формулой

.

Оптическая разность хода лучей, отраженных от двух поверхно­стей тонкой пленки, окруженной одинаковыми средами, определяется формулой

D = 2hn cos a - l₀/2.

В данном случае пленка окружена различными сре­дами - воздухом (n₁ = 1,0) и стеклом (n₂ = 1,7). Из неравенства n₁ < n < n ₂ следует, что оба луча 1 и 2, отражаясь от границы с оп­тически более плотной средой, «теряют» полуволну. Так как это не влияет на их разность хода, то следует отбросить слагаемое λ₀/2. Кроме того, полагая a = 0, получим

Δ = 2 hn.

Тогда толщина пленки

h = ±(2k + 1)l₀/4n.

Учитывая, что h - существенно положительная величина и что значению h_min соответствует k = 0, получим

h_min = λ₀ /4 n = 0,11 мкм.

 

 

B

A

C

a

a

1 2 1/ 2/

Пример 3. Между двумя плоскопараллельными стеклян- ными пластинками заключен очень тонкий воздушный клин. На пластинки нормально падает монохроматический свет (λ₀ = 0,50 мкм). Определить угол a между пластинками, если в отраженном свете на протяжении l = 1,00 см наблюдается N = 20 интерференционных полос.

 

Решение

В данном случае интерферируют лучи 1 и 2, отражен­ные от двух поверхностей тонкого воздушного клина (см. рис.). Наблюдаемые на поверхности клина интерференционные полосы будут полосами равной толщины, пред­ставляя собой геометрическое место точек, соответствующих одинаковой толщине клина.

Пусть точки А, В соответствуют двум соседним интерференцион­ным полосам. Проведя прямую ВС, парал- лельную нижней пластинке, и учитывая, что искомый угол весьма мал, имеем

(1)

где h_A, h_B — толщины воздушного клина в точках А, В.

Предпо­ложим для определенности, что АВ — расстояние между тем­нымиинтерференционными полосами. Тогда обе величины h_A, h_B най­дем, приравняв правые части формул и . Так как i₂ = 0, n = 1 (воздух) и h > 0, то

(2)

h = (k + 1) λ_0./2.

Поскольку величины h_A, h_B относятся к соседним полосам, то в фор­муле (2) числа k, соответствующие величи- нам h_A, h_B должны отли­чаться на единицу. Следовательно,

(3)

.

Легко, убедиться, что к такому же результату придем, предполо­жив, что АВ есть расстояние между соседними светлыми полосами. Теперь из формулы (1) с учетом результата (3) найдем

a = l₀N/2l = 5×10^-4 рад = 1¢40¢¢.

Пример 4. Сферическая поверхность плосковыпуклой линзы (n₁ = 1,52) соприкасается со стеклянной пластинкой (n₂ = 1,7). Пространство между линзой, радиус кри­визны которой R = 1 м, и пластинкой заполнено жидкостью. Наблю- дая кольца Ньютона в отраженном свете (λ₀ = 0,589 мкм), измерили радиус r_k десятого тем­ного кольца. Определить показатель преломления жид­кости n_ж в двух случаях:

1) r_k = 2,05 мм, 2) r_k = 1,9 мм.

Решение

Предположим, что показатель преломления жидкости n_ж удовлет­воряет одному из двух неравенств:

n_ж < n₁ < n₂; n₁ < п₂ < n_ж. (1)

Тогда для темных колец будет верна формула

.

Так как , получим n_ж = kRl₀ /r_k².

Выполнив вычисления, найдем:

1) n_ж1 = 1,41; 2) n_ж2 = 1,63.

Теперь пусть

n₁ < n_ж < n₂. (2)

В этом случае для темных колец верна формула

.

Тогда Выполнив вычисления, получим: 1) n_ж1 = 1,34; 2) n_{ж 2} = 1,55.

Сравнив результаты вычислений для обоих случаев (очевидно, соответствующих двум разным жидкостям), видим, что в первом случае (n_ж1 = 1,41; n_ж1 = 1,34) значения по­казателя преломления жидкости удовлетворяют одному из неравенств (1), но не удовлетворяют неравенству (2). Следовательно, для первой жидкости n_ж1 = 1,41. Во втором случае (n_ж2 = 1,63; n_{ж 2} = 1,55) выполняется только неравен- ство (2). Следовательно, для второй жидкости n_ж2 = 1,55.

Пример 5. На щель шириной а = 0,1 мм падает нормально монохроматический свет с длиной волны λ = 500 нм. Дифракционная картина проецируется на экран, параллельный плоскости щели, с помощью линзы, расположенной вблизи щели. Определить расстояние L от экрана Э до линзы, если расстояние l между первыми дифракционными минимумами, расположенными по обе стороны центрального максимума, равно 1 см.

Решение

φ

L

Э

l

 

Условие дифракционных минимумов от одной щели, на которую свет падает нормально

(1)

где по условию задачи, m = 1.

Из рисунка следует, что l = 2L tg φ, но так как l /2 << L, то tg φ = sin φ, откуда sin φ = l/2L.

Подставив эти значения в формулу(1), получим искомое расстояние от экрана до линзы:

Вычисляя, получим L = 1 м.

Пример 6. На дифракционную решетку нормально падает параллельный пучок лучей с длиной волны λ = 0,5 мкм. На экра­не, параллельном дифракционной решетке и отстоя- щем от нее на расстоянии L = 1 м, получается дифракционная картина. Расстояние между максимумами первого порядка, наблюдае­мыми на экране, оказалось равным r = 20,2 см.

Определить:

а) постоянную дифракционной решетки;

б) число штрихов на 1 см;

в) сколько максимумов дает при этом дифракционная решетка?

г) максимальный угол отклонения лучей, соответствую- щих последнему дифракционному максимуму.

Решение

а) Постоянная дифракционной решетки (а + b), длина волны λ и угол отклонения лучей φ, соответ­ствующий k -тому дифракционному максимуму, связаны соотно­шением

(a + b) sin φ = kλ, (1)

где k — порядок спектра. В данном случае k = 1, а

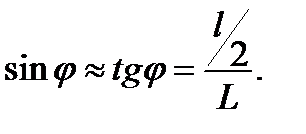
Указанное приближенное равенство имеет место, поскольку 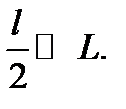Тогда соотношение (1) принимает вид

и см.

б) Число делений на 1 см найдем из формулы

см ^-1.

в)Для определения числа максимумов, даваемых дифрак­ционной решеткой, вычислим сначала максимальное значение k, которое определяется из условия, что максимальный угол от­клонения лучей дифракционной решеткой не может превы­шать 90°. Из формулы (1)

найдем искомое значение k_mах. Подставляя sin j = 1, получим k_max = 9,9.

Но так как k обязательно должно быть целым числом, то, следовательно, k_max = 9 (k не может принять значение, равное 10, так как при этом sin φ > 1).

Подсчитываем число максимумов, даваемых дифракционной решеткой: влево и вправо от центрального максимума будет наблюдаться одинаковое число максимумов, равное k_max, т. е. всего 2 k_max. Учитывая центральный (нулевой) максимум, полу­чим общее число максимумов

M = 2 k_max + 1= 19 максимумов.

г) Максимальный угол отклонения лучей, соответствую- щих последнему дифракционному максимуму, найдем, подставляя в формулу дифракционной решетки значение k = k_max

откуда находим искомое значение угла φ = 65°22'.

 

Пример 7. Определить длину волны монохрома- тического све­та, падающего нормально на дифракционную решетку с периодом d = 2,20 мкм, если угол между максимумами первого и второго порядков спектра Δφ = 15°.

Решение

Пусть φ ₁, φ ₂ - углы дифракции, соответствующие максимумам первого (k = 1) и второго (k = 2) порядков. По уcловию

φ ₂ - φ ₁ = Δ φ. (1)

 

Из формулы дифракционной решетки следует

d sin φ₁ = λ, (2)

d sin φ₂ = 2 λ. (3)

Система уравнений (1), (2), (3) содержит три неизвестных: φ₁, φ₂, λ. Разделив почленно (2), (3), получим sin φ₂ = 2 sin φ₁, или, учи­тывая (1),

sin (φ₁ + Δ φ) = 2 sin φ₁.

Решив это тригонометрическое уравнение относительно sin φ₁, найдем

(4)

Теперь из (2) с учетом (4) определим искомую величину:

мкм.

Пример 8. При каком минимальном числе штрихов дифрак­ционной решетки с периодом d = 2,9 мкм можно раз­решить компоненты дублета желтой линии натрия (λ₁ = 5890 и λ₂ = 5896 )?

Решение

Число штрихов N решетки связано с ее разре­шающей силой R и порядком спектра k соотношением R = kN, от­куда следует: N = R/k. Минимальному значению N_мин соответст­вует минимальное значение R_мин и максимальное число k, т. е.

N_мин = R_мин /k_макс.

Минимальная разрешающая сила решетки R_мин, необходи- мая для разрешения дублета (двух составляющих) желтой линии нат­рия, выражается через величины λ₁ и λ₂ по формуле:

R_мин = l₁ / (l₂ - l₁).

Число k_макс найдем из формулы дифракционной решетки, если положим в ней sin φ = 1 и λ = λ₂ (последнее соотношение га­рантирует, что обе компоненты дублета с порядковым номером k_макс будут видны). Учитывая при этом, что k — целое число, получим

Тогда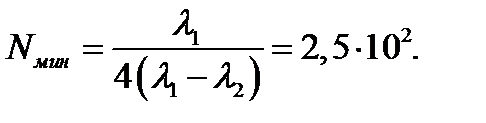

Пример 9. Пучок естествен­ного света падает на полиро­ванную поверхность стеклянной пластины, погруженной в жид­кость. Отраженный от пластины пучок света образует угол φ = 97° с падающим пучком. Определить показатель прелом­ления n₁ жидкости, если отра­женный свет максимально поляризован.

Решение

Согласно за­кону Брюстера, пучок света, отраженный от диэлектрика, максимально поляризован в том случае, если тангенс угла падения численно равен относительному показателю пре­ломления

j n1 n2

где n ₂₁ - показатель преломления вто­рой среды (стекла) относительно первой (жидкости).

Относительный показатель преломления равен отно­шению абсолютных показателей преломле- ния. Следова­тельно,

Так как угол падения равен углу отражения, то e = φ /2 и, следовательно, tg(j /2) = n ₂/ n ₁, откуда

Пример 10. Два николя N ₁и N ₂ расположены так, что угол между их плоскостями пропускания составляет a = 60°. Определить, во сколько раз уменьшится интен­сивность I₀ естественного света: 1) при прохождении через один николь N ₁; 2) при прохождении через оба николя. Коэффициент поглощения света в николе k = 0,05. Потери на отражение света не учитывать.

Решение

1. Естественный свет, падая на грань призмы Николя, расщепляется вследствие двойного лучепреломления на два пучка: обыкновенный и необыкновенный. Оба пучка одинаковы по интенсив­ности и полностью поляризованы.

Естественный луч света

N1 I1=0,5I0(1-k)

N2 I2=0,5I0(1-k)2cos2α

A e   o B

o   e

 

Обыкновенный пучок света (о) вследствие полного отражения от границы АВ отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный пучок (е) проходит через призму, уменьшая свою интен­сивность вследствие поглощения. Таким образом, интен­сивность света, прошедшего через первую призму,

I ₁ = ½ I ₀ (1-k).

Относительное уменьшение интенсивности света полу­чим, разделив интенсивность I ₀естественного света, падающего на первый николь, на интенсивность I ₁поля­ризованного света:

Таким образом, интенсивность уменьшается в 2,1 раза.

 

2. Плоскополяризованный пучок света интенсивности I ₁ падает на второй николь N ₂и также расщепляется на два пучка различной интенсивности: обыкновенный и необыкновенный. Обыкновенный пучок полностью погло­щается призмой, поэтому его интенсивность нас не интересует. Интенсивность I₂ необыкновенного пучка, вышедшего из призмы N₂, определяется законом Малюса (без учета поглощения света во втором николе):

I₂ = I₁ cos² a,

где a - угол между плоскостью колебаний в поляризо­ванном пучке и плоскостью пропускания николя N₂.

Учитывая потери интенсивности на поглощение во втором николе, получаем

I₂ = I₁ (1-k) cos² a,

Искомое уменьшение интенсивности при прохождении света через оба николя найдем, разделив интенсив­ность I₀ естественного света на интенсивность I ₂ света, прошедшего систему из двух николей:

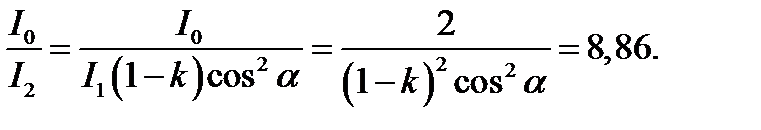
Таким образом, после прохождения света через два николя интенсивность его уменьшится в 8,86 раза.

 

Пример 11. На пути частично поляризованного пучка света поместили николь. При повороте николя на угол φ = 60° из положения, соответствующего максималь­ному пропусканию света, интенсивность прошедшего света уменьшилась в n = 3 раза. Найти степень по­ляризации падаю- щего света.

Решение

Частично поляризованный свет можно рассмат­ривать как смесь плоскополяризованного и естественного света. Ни­коль всегда пропускает половину падающего на него естественного света (превращая его в плоскополяризованный). Степень пропускания поляризованного света, падающего на николь, зависит, согласно за­кону Малюса

от взаимной ориентации главных плоскостей поля­ризатора и анализатора. Поэтому полная интенсивность света, про­шедшего через николь,

I = 0,5 I_n + I_p cos² φ,

где I_n, I_p - интенсивности естественной и поляризованной состав­ляющих света, падающего на николь.

Степень поляризации света

,

где I_макс = 0,5 I_n + I_p, I_мин = 0,5 I_n.

По условию, I_макс = kI, или,

I_макс =kI_мин + (I_макс - I_мин) cos² φ.

Обозначим через a отношение I_макс / I_мин, тогда

P = ( 1 -a)/ ( 1 +a);

1 = k [ a + (1 - a) cos² j ];

 

6. КВАНТОВАЯ ОПТИКА

 

Волновые представления о природе света позволили объяснить такие явления, как интерференция, дифракция, поляризация и дисперсия света. Важным подтверждением этих представлений стали электродинамика Максвелла и экспериментальное доказательство электромагнитной природы света. Однако во второй половине века при изучении некоторых явлений было обнаружено, что выводы, получен- ные на основе волновой теории, противоречат эксперимен- тально установленным законам. Простейшими примерами таких явлений служат тепловое излучение и внешний фотоэффект. Корректное объяснение было получено лишь на основе квантовых представлений о природе света: излучение и поглощение света происходит отдельными порциями энергии – квантами или фотонами. Эти представления привели к понятию корпускулярно-волнового дуализма и развитию квантовой физики. Рассмотрим подробнее явления и процессы, в которых свет проявляет квантовые свойства.