Уравнение (1) называется уравнением регрессии Y на Х; функция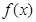 
называется регрессией Y на Х, а ее график - линией регрессии Y на Х. Функция 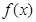может иметь разный вид: она может быть линейной, квадратичной, экспоненциальной и т.д. Поэтому п ервая задача теории корреляции - установить форму корреляционной связи, т.е. вид функции регрессии. Чаще всего принимается, что функция регрессии является линейной. Если функция регрессии 
линейна, то корреляцию называют линейной; в противном случае - нелинейной. Очевидно, при линейной корреляции линия регрессии являются прямой линией.
Вторая задача теории корреляции - оценить тесноту (силу) корреляционной связи. Теснота корреляционной зависимости Y от X оценивается по величине рассеяния значений Y вокруг условного среднего 
. Большое рассеяние свидетельствует о слабой связи Y и X или даже об отсутствии зависимости. Малое рассеяние указывает на наличие достаточно сильной зависимости; возможно даже, что Y и X связаны функционально, но под действием второстепенных случайных факторов эта связь оказалась размытой, в результате чего при одном и том же значении х величина Y принимает разные значения.
Наглядно на графике тесноту связи можно оценить при помощи построения корреляционного поля. Действительно, для изучения корреляционной зависимости необходимо измерить два параметра у одного объекта (человека, животного и т.д.). Такие выборки называются связанными, поскольку числа в строках таблицы связаны или фамилией испытуемого или номером животного. Откладывая один из параметров на оси абсцисс, а другой на оси ординат, мы можем изобразить каждый объект в декартовой системе координат точкой на плоскости. Тогда все исследование изобразится некоторым распределением точек на плоскости. Оценивая тесноту расположения этих точек и их направленность, можно приблизительно оценить как вид корреляционной зависимости (линейная или нелинейная), так и оценить силу связи.
Например, в таблице 1 приведены результаты следующего эксперимента. Было сделано предположение, что чем выше уровень тревожности студента перед тестированием, тем больше он занимается и, следовательно, получает более высокие результаты тестирования. Исследование было проведено на 36 студентах. (Пример взят из Наследов А. Компьютерный анализ данных в психологии и социальных науках. Санкт-Петербург, «Питер», 2007, 416 с.)
Таблица 1
| уровень тревожности (баллы) | ||||||||||||
| результат теста (баллы) |
На рисунке 1 результаты исследования приведены в графическом виде. Как видно из рисунка, корреляция между результатами тестирования и уровнем тревожности достаточно высокая, поскольку точки располагаются достаточно тесно друг к другу. Далее, очевидно, что это не линейная корреляция, а, скорее всего квадратичная, поскольку распределение точек имеет хорошо выделяемый максимум. Из рисунка также видна еще одна закономерность: при малых значениях уровня тревожности действительно с ростом уровня тревожности растут результаты тестирования, но когда уровень тревожности превышает 7 баллов, дальнейший рост уровня тревожности приводит к уменьшению результатов тестирования.
Рис 1. Корреляционное поле, демонстрирующее зависимость результатов тестирования от уровня тревожности
На рисунке 2 приведены примеры корреляционных полей в случае линейной корреляции и указаны оценки тесноты связи и вида связи (см. ниже), соответствующие тому или иному корреляционному полю.
Рис 2. Корреляционные поля и соответствующие им оценки тесноты связи и вида связи
