Две случайные величины могут быть связаны функциональной зависимостью, быть независимыми, либо статистически зависимыми.
Если значению одной величины соответствует строго определенное значение другой величины, то зависимость между ними называется функциональной. Функционально связанные случайные величины х и у могут принимать различные значения, но если х приняла определенное значение, то у соответствует ему однозначно.
Статистической зависимостью величины у от величины х называется зависимость при которой каждому значению величины х из множества её возможных значений соответствует некоторое множество возможных значений величины у, характеризуемое определенным законом распределения.
Частным случаем статистической зависимости является корреляционная (или стохастическая). Понятие корреляции соответствует русскому термину «соотношение».
Основные регулирующие системы организма непрерывно осуществляют стабилизацию всех параметров. При возникновении патологии (или при изменении внешних воздействий) изменение значения одного параметра влечет за собой изменения в различной степени значений других параметров. В силу наличия обратных связей и множественности путей саморегуляции организма связь между его параметрами является случайной и может быть описана не функциональной зависимостью, а корреляционной связью. Выявление связей (корреляций) между различными случайными параметрами и случайными процессами широко используется в медицинской диагностике.
Благодаря различным формам корреляции (физико-химическим, нервным, морфофизиологическим, эволюционным и т.д.) организм проявляется как единая сложная целостная система.
Корреляция обозначает главным образом степень выраженности связи между вариационными рядами. Например, между массой тела человека и объемом циркулирующей крови, между основным обменом веществ и амплитудной артериального давления. Уже в 1637 г. Галилей обсуждал связь между размерами скелета и массой организма.
2. КОРРЕЛЯЦИОННОЕ ПОЛЕ, ЛИНИИ И УРАВНЕНИЯ РЕГРЕССИИ
Наглядно корреляционная зависимость может быть выражена графически. На осях абцисс и ординат откладываются значения вариационных рядов. Для каждого отдельного наблюдения получают значения в каждом из вариационных рядов. Эти значения (при данном наблюдении) соответствуют друг другу и их совокупность обозначается точкой на плоскости. Число таких точек оказывается равным числу наблюдений. Совокупность точек на плоскости называется корреляционным полем, оно создаёт общую картину корреляции и обычно позволяет построить усреднённую кривую – линию регрессии – взаимосвязи параметров, составляющих два вариационных ряда.
Если между величинами существует связь, то корреляционное поле имеет вид элипса со сгущениям точек вокруг главной оси и их малым числом на периферии (рис. 1).
Рис 1. Линия регресии rx,y>0, Рис 2. Отсутствие корреляционной связи rx,y=0
Если связь выражена слабо, то разброс точек велик (рис. 2).
При корреляционной зависимости изменение одной из величин влечет изменение математического ожидания другой. Эту зависимость можно записать в помощью уравнения вида:
- уравнение регрессии у на х.
- это условное математическое ожидание величины у, соответствующее данному значению х.
х - отдельные значения величины х.
f(x) - некоторая функция
- уравнение регрессии х на у.
Функции f(x) и f(у) называют регрессиями у на х и х на у соответственно. Графики этих функций называются линиями регрессии.
Корреляционная зависимость может быть линейной, квадратической, экспоненциальной и т.д.
Если f(x) и f(у) – линейные функции, то уравнения регрессии имеют вид:
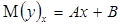
где А, В, С, Д – это некоторое параметры. Для определения этих параметров применяют метод наименьших квадратов (рассматривать не будем).
