Задача №1: В течение 10 минут на диспетчерский пункт может поступить 0 вызовов с вероятностью 0,2; 1 вызов с вероятностью 0,2; 2 вызова с вероятностью 0,4; 3 вызова с вероятностью 0,1; 4 вызова с вероятностью 0,1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа вызовов за 10 минут.
Решение: Для решения удобно составить таблицу:
| Число вызовов хi | ∑ | |||||
| Вероятность Pi | 0,2 | 0,2 | 0,4 | 0,1 | 0,1 | |
| xiPi | 0,2 | 0,8 | 0,3 | 0,4 | 1,7 | |
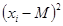
| 2,89 | 0,49 | 0,09 | 1,69 | 5,29 | - |
| 0,578 | 0,098 | 0,036 | 0,169 | 0,529 | 1,41 |
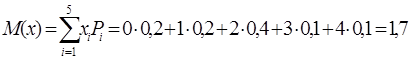
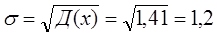
Задача №2. Амплитуда вызванных биопотенциалов мозга (мкВ) хi появилась с частотой mi:
| Амплитуда биопотенциалов (мкВ) (хi) | 2,3 | 4,0 | 7,4 | 4,5 | 6,7 | 10,0 | 9,2 |
| mi |
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и вероятность, что величина амплитуды вызванного биопотенциала мозга Dφ≤5 мкВ.
Решение
Для нахождения математического ожидания М дискретного ряда распределения используем формулу: 
где хi- значения вариант ряда;
Рi - вероятность (относительная частота появления варианты).
Вероятность Рi - определяем по формуле:
где n -объем выборки, равный 
-частота появления i варианты.
Дисперсию Д определяем по формуле:
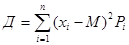
Среднее квадратическое отклонение σ определяем по формуле:
Заполним таблицу:
| хi (мкВ) | 2,3 | 4,0 | 7,4 | 4,5 | 6,7 | 10,0 | 9,2 | |
| mi | 
| |||||||
| 0,06 | 0,17 | 0,29 | 0,23 | 0,11 | 0,06 | 0,09 |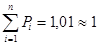 
(условие нормировки)
|
| хi Pi | 0,14 | 2,15 | 1,04 | 0,74 | 0,60 | 0,83 | 
| |
| 0,91 | 0,82 | 0,42 | 0,66 | 0,03 | 0,87 | 0,81 | 
|
Определяем среднее квадратическое отклонение σ:
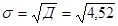=2,13 (мкВ).
Находим вероятность того, что значение биопотенциала мозга Dφ≤5 мкВ, по формуле:
где х=Dφ≤5 мкВ
Функция распределения от отрицательного параметра (-z) определяется выражением:
Таким образом:
Значение Ф(z) определяется по таблице: “Значения нормальной функции распределения” (см. приложения №3).
Ответ: М=6,2 мкВ; Д=4,52(мкВ)2; σ=2,13 мкВ
Р= 0,2877≈29%
Задача №3. Измерения значений естественного фона ионизирующего излучения в импульсах/сек, полученные с помощью пересчетного прибора, дали следующие результаты:
15 19 20 20 21 23 24 16 27 40 30 31 32
35 25 26 30 30 20 28 26 23 18 12 10
Удовлетворяет ли это распределение распределению Гаусса? Построить графики зависимости экспериментальной вероятности попадания значений в каждый из интервалов Рi и теоретической вероятности Ртеор от средних значений интервалов 
.
Решение: Из полученных результатов составляем вариационный ряд:
10 12 15 16 18 19 20 20 20 21 23 23 24
25 26 26 27 28 30 30 30 31 32 35 40
Все варианты выборки делят в зависимости от числа вариант на нечетное число интервалов, начиная с трех (k=3, 5, 7, 9, 11, …).
Разобъём вариационный ряд на 5 интервалов. Находим шаг интервала 
:
,
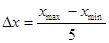где 
-максимальное значение варианты в интервале,
-минимальное значение варианты в интервале.
Тогда 
Верхние границы каждого из интервалов определяется по формуле:
где i =1, 2, 3, 4, 5, (i -номер интервала)
Нижняя граница каждого последующего интервала 
определяется значением верхней границы предыдущего.
Вероятность попадания варианты в данный интервал Рi (экспериментальная вероятность) определяется по формуле:
где 
-число вариант в каждом из интервалов, определяемых по вариационному ряду, исходя из значений нижней и верхней границы интервала.
-обьем выборки, в нашей задаче равный 25.
Среднее значение интервала определяем по формуле:
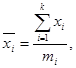
где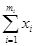 
-сумма значений вариант в интервале.
Математическое ожидания М определяем по формуле:
,
Дисперсию Д определяется по формуле:
,
Среднее квадратическое отклонение 
Учитывая все вышеуказанное, заполняем таблицу №1.
Таблица 1.
| № интервала | (имп/сек)
| 
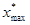(имп/сек)
|
| Рi |
(имп/сек)
| 
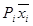(имп/сек)
| 
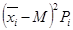(имп/сек)2
|
| 0,16 | 13,25 | 2,12 | 18,63 | ||||
| 0,24 | 19,67 | 4,72 | 4,58 | ||||
| 0,32 | 25,25 | 8,08 | 0,47 | ||||
| 0,20 | 30,60 | 6,12 | 8,61 | ||||
| 0,08 | 37,50 | 3,00 | 14,49 | ||||
| М =24,04 | Д =46,78 |
Примечание. Количество вариант первого интервала определяем, исходя из того, что нижней границией является 10 имп/сек, а верхней – 16 имп/сек, т.е. в первый интервал из вариационного ряда вошли варианты:
10; 12; 15; 16 (
), среднее значение этого интервала:
.
Во второй интервал вошли варианты: 18; 19; 20; 20; 20; 21. Таким образом, m2=6, тогда
и т.д.
Среднее квадратическое отклонение 
равно:
.
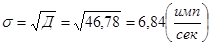Для определения теоретической вероятности попадания варианты в данный интервал находим значения функции распределения Ф(z2) и Ф(z1), где 
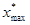( -верхняя граница соответствующего интервала)
(
нижная граница соответствующего интервала).
Если значения z отрицательное, то Ф(-z)=1-Ф(z)
Значение теоретической вероятности попадания варианты в интервал Ртеор определяем по формуле:
Ртеор=Ф(z2)-Ф(z1).
Величина функции распределения Ф(z) определяется по таблице (см. приложение №3).
Полученные значения z2, Ф(z2), z1, Ф(z1) и Ртеор=Ф(z2)-Ф(z1) заносим в таблицу №2.
Таблица №2
| № интервала | 
| Ф(z2) | 
| Ф(z1) | Ртеор=Ф(z2)-Ф(z1) |
| -1,18 | 0,1190 | -2,05 | 0,0179 | 0,10 | |
| -0,30 | 0,3821 | -1,18 | 0,1190 | 0,26 | |
| 0,58 | 0,7190 | -0,30 | 0,3821 | 0,34 | |
| 1,46 | 0,9279 | 0,58 | 0,7190 | 0,21 | |
| 2,33 | 0,9893 | 1,46 | 0,9279 | 0,06 |
Сравнивая величины для каждого из пяти интервалов экспериментальной вероятности Рi (см. таблицу №1) и теоретической вероятности попадания варианты в заданный интервал Ртеор (см. таблицу №2), можно сделать вывод, что их значения очень близки друг к другу, следовательно, полученные значения естественного фона подчиняются распределению Гаусса.
Строим графики зависимости экспериментальных вероятностей Рi и теоретических вероятностей Ртеор от средних значений интервалов 
экспериментальная кривая
теоретическая кривая.
ПРАКТИЧЕСКАЯ ЧАСТЬ
