Закон распределения случайной величины

Итак, мы приходим к задаче: как найти вероятность, что при следующем испытании случайная величина попадет в наперед заданный интервал?

Для ответа на этот вопрос, прежде всего надо ввести понятие закона распределения случайной величины.

Закон распределения случайной величины (ЗРСВ) – это способ рассчитать вероятность того, что случайная величина (СВ) примет то или иное значение (для дискретных случайных величин) или попадет в тот или иной интервал (для непрерывных случайных величин) в результате испытания.

Для дискретных СВ это чаще всего таблица. Например, для правильной игральной кости эта таблица будет выглядеть так:

 

1/6	1/6	1/6	1/6	1/6	1/6

Выпадение 1, 2, 3, 4, 5, или 6 равновероятно и равно одной шестой.

Для непрерывной случайной величины, ЗРСВ может быть задан или в виде графика или в виде формулы. Наибольшее значение в математической статистике имеет нормальный закон распределения случайной величины или закон Гаусса.

Это связано с тем, что очень многие СВ распределены именно по этому закону, в том числе и в биологии и медицине.

Итак, для вычисления вероятностей нам нужен закон Гаусса. Рассмотрим этот закон.

Поставим задачу более точно. Пусть у нас есть некоторая непрерывная случайная величина Х и мы хотим узнать какова вероятность, что при следующем испытании эта величина примет значение х_i, лежащие в маленьком интервале от х до х+dx (здесь dx – дифференциал х). Тогда вероятность P(x_i), что при следующем испытании это произойдет, по закону Гаусса будет равна:

(1)

Формула (1) позволяет рассчитать вероятность попадания следующего измерения в бесконечно маленький интервал dx. Но на практике нам надо научиться рассчитывать вероятность попадания в реальные интервалы, например в интервал от х=а до х=b. Это можно сделать с помощью формулы (2):

 

(2)

Поскольку интервал (а,b) мы задаем сами, следовательно, для расчета вероятности того, что результат следующего испытания попадет в этот интервал нам надо знать только два числа: μ - математическое ожидание и σ - среднее квадратическое отклонение.

Таким образом, оценка этих двух чисел является одной из основных задач математической статистики.

Итак, чтобы решить главную задачу, которая как мы знаем, состоит в том, чтобы научиться рассчитывать вероятность попадания случайной величины в тот или иной наперед заданный интервал, нам надо научиться рассчитывать эти два числа. Вот здесь нас ожидает неудача, поскольку точно рассчитать эти два числа оказалось невозможным! Оказалось, что для того чтобы точно получить эти два числа, например для случайной величины «рост», надо измерить рост у всех людей в мире! Ясно, что мы этого сделать не можем. Что же нам остается? А остается нам измерить рост у тех людей, до которых мы можем добраться, и по полученным значениям ОЦЕНИТЬ значения μ и σ. Подчеркну: не получить точные значения, а только оценить чему приблизительно они равны. Вот эти оценки, которые называются выборочным арифметическим средним () и оценкой среднеквадратичного отклонения (s) и являются самой первой целью большинства статистических исследований.

В нашем рассмотрении неожиданно появилось слово «выборочная». Попробуем объяснить, что оно значит. Для этого введем следующее определение:

Совокупность объектов, из которой отбирается некоторая часть ее членов для изучения, называется генеральной, а отобранная тем или иным способом часть генеральной совокупности называется выборочной совокупностью или выборкой.

В случае с ростом генеральной совокупностью является рост всех людей, тогда как те люди, у которых мы смогли измерить рост, называются выборкой из этой совокупности. Очевидно, что это определение справедливо для любой случайной величины.

РАСЧЕТ И S.

Расчет этих двух величин очень прост и задается следующими двумя формулами:

(3)

 

(4)

 

Чтобы пояснить формулы (3) и (4), представим себе, что мы измеряли рост у 50 человек. Это значит что n=50. Далее складываем все 50 полученных чисел и полученный результат делим на 50. Получаем значение среднего арифметического. Это все расчеты по формуле (3). Расчеты по формуле (4) несколько сложнее. Сначала от всех полученных в результате измерений 50 чисел отнимаем ранее полученную оценку среднего. Получаем 50 значений разности. Потом все 50 разностей возводим в квадрат, после чего все их складываем. Полученный результат делим на 49 (n-1). Из того что получилось, извлекаем квадратный корень. Расчеты среднего арифметического и оценки среднеквадратичного отклонения закончены.

Теперь, когда мы имеем оценки среднего и среднеквадратичного отклонения нам необходимо вернуться к формуле (2). Действительно, оценки μ и σ у нас есть, интервал (а,b) задаем сами, осталось взять интеграл... Но здесь нас подстерегает новая неприятность! Неопределенный интеграл такого вида не берется в элементарных функциях. На наше счастье мы имеем дело не с неопределенным интегралом, а с определенным интегралом. Как мы помним из предыдущего курса, определенный интеграл есть число и существует достаточно много численных методов получения этого числа с любой наперед заданной точностью. Применив один из этих методов, мы получим число, которое и будет вероятностью попадания следующего измерения случайной величины в интервал (a,b). Изменив границы интервала и проведя аналогичные расчеты мы получим вероятность попадания случайной величины в этот новый интервал и т.д. Задача вроде бы решена. У нас есть методика расчета вероятности попадания случайной величины в любой наперед заданный интервал. Однако проведение таких расчетов не очень удобно, поскольку требует много вычислений. Можно ли облегчить себе жизнь? Ну, первое, что приходит на ум это рассчитать все значения интеграла для интервалов, изменяющихся с определенным (небольшим шагом) и занести их в таблицу. Тогда можно пользоваться этой таблицей и ничего не считать. Но эта таблица будет верна, только для той случайной величины, для которой она рассчитывалась. Получается, что нам надо создавать бесчисленное количество таблиц для всевозможных случайных величин. Ясно, что здесь тоже надо что-то придумать. Человечество придумало, как обойтись одной таблицей для всех случаев. Для этого от нашей случайной величины X (любой, которую мы изучаем) надо перейти к другой случайной величине Z, используя следующее соотношение:

(5)

Что же мы получим в результате этой операции? Мы получим новую случайную величину, для которой = 0 и s = 1. Эта случайная величина называется нормированной нормально распределенной случайной величиной Z. Поскольку эту операцию можно провести для ЛЮБОЙ случайной величины, подчиняющейся закону Гаусса, мы можем любую случайную величину свести к случайной величине Z, а, следовательно, для расчета вероятности попадания исходной случайной величины в наперед заданный интервал построить ТОЛЬКО ОДНУ таблицу. Конечно же, такая таблица была давно построена, она приведена в приложении 3 и называется таблицей значений функции распределения нормированной нормально распределенной случайной величины

.(6).

Научимся пользоваться этой таблицей. Например рассмотрим число стоящее на пересечении строки, начинающейся с 0,5 и столбца, помеченного цифрой 5. Это число равно 0,7088. Оно показывает, что при следующем испытании вероятность что случайная величина примет значение МЕНЬШЕ 0,5 5 равна 0,7088. Обратите внимание, что номер столбца есть сотый знак заданного нами числа. Теперь поставим задачу так. Как пользуясь таблицей найти вероятность попадание в интервал (z₁,z₂), ведь это и есть наша основная задача. Если z₂ > z₁, то искомая вероятность будет равна разности Ф(z₂)–Ф(z₁). Например, найдем вероятность, что при следующем испытании значение нормированной случайной величины попадет в интервал (0,95; 1,54). Сначала найдем Ф(1,54). Для этого найдем в таблице строку, которая начинается с 1,5, потом двигаемся по этой строке до столбца, помеченного цифрой 4. Там стоит значение Ф(1,54) = 0,9382. Аналогичным образом найдем Ф(0,95) = 0,8289. Тогда искомая вероятность будет равна: Р = 0,9382 – 0,8289 = 0,1093.

Для полного решения поставленной задачи осталось ответить только на один вопрос: а что если значения z получатся отрицательные? Ведь в таблице приложения 3 нет отрицательных значений. Ответ на этот вопрос дает следующая формула:

Ф(-z) = 1 – Ф(z) (7).

Из формулы (7) следует: если z получилось отрицательным, то надо найти значение Ф(z) по таблице считая z положительным, а потом найденное значение отнять от единицы, это и будет ответом. Теперь задача нахождения вероятности попадания случайной величины, распределенной по закону Гаусса, в любой наперед заданный интервал решена полностью

Для иллюстрации введенных в рассмотрение понятий разберем следующий пример. Пусть в родильном доме за сутки родилось 20 детей, вес которых с точностью до 0,1 килограмма приведен в таблице 1.

Таблица 1

Вес новорожденных в килограммах

X	1,8	2,1	3,1	4,2	3,6	2,2	3,1	3,9	4,4	2,6
3,3	3,8	3,3	4,8	2,8	3,6	3,4	2,8	3,7	3,2

 

Надо рассчитать какова вероятность, что вес первого новорожденного в следующие сутки будет находиться между двумя и тремя килограммами.

Итак, в формуле (2) a=2, b=3

1. По формулам (3) и (4) найдем среднее арифметическое и оценку среднеквадратического отклонения: Получим следующие значения:
2. Для нижней границы интервала (а=2) построим значение z по формуле (5).
3. Тоже самое сделаем для верхней границы:
4. Найдем Ф(-0,42). Для этого в таблице приложения 3 найдем сначала Ф(0,42) = 0,6628. Тогда Ф(-0,42) = 1 – 0,6628 = 0,3372.
5. Теперь найдем Ф(-1,86). Аналогично предыдущему Ф(1,86)= 0,9686 и Ф(-1,86) = 1 – 0,9686 = 0,0314
6. Таким образом, вероятность, что следующим родиться ребенок с весом в интервале от 2 до 3 кг равна Р = 0,3372 – 0,0314 = 0,3058

Задача 2.

Решение первой задачи хотя и важно, но конечно не достаточно для практических целей. Следующей важнейшей задачей статистики является получение ответа на вопрос можно ли считать, что какой-то эффект действительно существует или необходимо признать, что на самом деле эффекта нет, и все, что мы наблюдаем есть игра случая. Под эффектом может подразумеваться все что угодно, например, действительно ли жители Скандинавии выше ростом жителей Африки, действительно ли одно лекарство эффективнее другого, действительно ли физиологические параметры изменяются в процессе адаптации, действительно ли успеваемость в одном классе выше успеваемости в другом и т.д.

Очевидно, что все эти задачи нацелены на сравнение двух выборок. Встает вопрос как это сделать. Допустим, мы измеряли рост 10000 жителей Скандинавии и 10000 жителей Африки. Таким образом, мы имеем два набора по 10000 чисел. Ясно, что просто разглядывая эти числа, мы мало чего добьемся. Возникает потребность описать каждый из наборов небольшим количеством производных от них параметров и уже потом сравнивать не сами числа, входящие в тот или иной набор, а эти вновь полученные параметры, характеризующие каждый из наборов. Поскольку вновь полученные параметры описывают сделанную выборку, они получили название «описательные статистики». Описательные статистики можно разделить на несколько групп. Мы будем рассматривать две из них: меры центральной тенденции и меры рассеивания.

Меры центральной тенденции характеризуют центральное значение, вокруг которого распределены значения случайной величины. К ним относятся средняя арифметическая (введена в рассмотрение в предыдущем разделе) и медиана. Средняя арифметическая хорошо подходит для описания распределений, близких к нормальным. Если же распределение существенно отличается от нормального (например, имеет очень длинные и широкие хвосты), то в этом случае имеет смысл использовать для оценки "центрального" значения медиану.

Как рассчитать среднюю арифметическую мы уже знаем (см. формулу (3) предыдущего раздела). Остановимся на медиане.

Медиана распределения какой-либо случайной величины X – это такое число Me, для которого вероятность, что при следующем испытании получиться значение исследуемой случайной величины больше Me равно 1/2. Это означает, что вероятность получить значение меньше или равно Me также равна 1/2. Таким образом, медиана характеризует центр распределения в том смысле, что появление значений больше медианы и меньше медианы равновероятны.

Теперь рассмотрим алгоритм, как по значениям выборки оценить медиану. (Обратите внимание на слово «оценить»).

Первое, что надо сделать, это отранжировать, т.е. расположить по возрастающей все значения выборки. Если мы проделаем эту процедуру с выборкой, представленной в предыдущем разделе, то мы получим следующую таблицу:

 

X	1,8	2,1	2,2	2,6	2,8	2,8	3,1	3,1	3,2	3,3
3,3	3,4	3,6	3,6	3,7	3,8	3,9	4,2	4,4	4,8

Далее необходимо определить четное или нечетное число значений в выборке. Если число значений нечетное, то медиана равна значению, находящемуся в центре выборки, если число значений четное, то медиана равна полусумме значений, стоящих в центре выборки. В нашем случае число значений в выборке равно 20, т.е. четное. На 10-м месте стоит число 3,3, а на 11 месте также стоит число 3,3. Следовательно, медиана равна: . В нашем случае получилось, что медиана и среднее арифметическое равны, но это не всегда так.

Меры рассеивания характеризуют разброс, с которым случайная величина распределяется вокруг своего центрального значения. К этим мерам относятся дисперсия, среднеквадратичное отклонение (введено в рассмотрение в предыдущем разделе), стандартная ошибка среднего, коэффициент вариации.

Если за центральное значение взять среднее арифметическое, то оценку дисперсии можно вычислить по следующей формуле:

(8).

Для нашего случая

Как видно из сравнения формул (4) и (8) оценка среднеквадратичного отклонения связана с оценкой дисперсии следующим соотношением:

(9)

В нашем случае .

Большое значение в медицине при проведении расчетов играет такая мера разброса как стандартная ошибка среднего (m), поскольку результаты проведенных исследований часто представляются в виде: . Формула для расчета оценки стандартной ошибки среднего задается следующим простым соотношением:

(10)

Для нашего случая

Изложенные выше меры рассеивания (дисперсия, среднеквадратичное отклонение, стандартная ошибка среднего) имеют один недостаток: они дают показатель изменчивости признака в именованных величинах, а не в относительных. Например, для выборки, представленной в Таблице 1, дисперсия будет выражаться в кг², а среднеквадратичное отклонение и стандартная ошибка в килограммах. Поэтому сопоставление (или сравнение) разноименных признаков по этим параметрам невозможно. Например, если бы мы измеряли не только вес новорожденных, но и их рост, то используя эти меры разброса нельзя было бы ответить на вопрос где изменчивость больше: в случае веса или в случае роста.

Для сравнения изменчивости двух разноименных выборок удобно пользоваться коэффициентом изменчивости (вариации) признака, который выражается в относительных величинах, а именно в процентах, и вычисляется по формуле:

(11).

В нашем случае

Чем больше V, тем более изменчив признак. Значения коэффициента вариации, невыходящие за пределы 10%, принято считать нормальными.

Если V>20%, то выборка некомпактна по заданному признаку.

Теперь, когда мы ввели в рассмотрение описательные статистики, задачу определить есть эффект или нет эффекта можно свести к вопросу различаются ли какие либо описательные статистики одной выборки от другой.

Казалось бы решение вопроса очень простое: посчитай описательные статистики одной и второй выборки и сравни их друг с другом. Однако дело обстоит далеко не так просто. Действительно, если бы мы измеряли вес не 20 новорожденных, а скажем, к примеру, только 19, было бы значение среднего и всех остальных описательных статистик тем же самым? Скорее всего НЕТ! Как говорилось, выше мы же всегда имеем дело с выборкой, а не с генеральной совокупностью, поэтому мы всегда получаем ОЦЕНКИ описательных статистик, а не их истинные значения. Следовательно, для решения поставленной задачи нельзя делать выводы, сравнивая непосредственно сами значения. Как же тогда решить задачу?

На помощь приходит понятие доверительного интервала. Идея доверительных интервалов возникает из вопроса: хорошо, мы не знаем точного значения той или иной описательной статистики, но мы хотя бы можем задать интервал, в котором оно находится? Ответ на этот вопрос таков: да мы можем построить интервал, внутри которого содержится точное значение той или иной описательной статистики с наперед заданной вероятностью. Таким образом, мы можем построить доверительный интервал, в котором точное значение описательной статистики содержится с вероятностью, например, 80% или 90%, или 95% или 99% и т.д.

Рассмотрим построение доверительного интервала для среднего значения. В этом случае получается следующее соотношение:

-mt < μ < +mt (12)

В формуле (12) -среднее арифметическое, μ – математическое ожидание (это и есть «истинное» значение, смотри (2)), m – стандартная ошибка среднего (см. (10)). Остается разобраться, что такое t. Буквой t обычно обозначается значение распределения Стьюдента. Расчет конкретного значения распределения Стьюдента для какого-либо конкретного случая довольно сложная задача, поэтому это распределение уже давно затабулировано и представлено в таблице приложения 4.

Рассмотрим эту таблицу. Для отыскания нужного нам значения надо, прежде всего, ответить для себя на вопрос: с какой вероятность мы собираемся строить доверительный интервал? В приложении 4 приведена таблица, которая позволяет строить доверительные интервалы с вероятностями 0,95, 0,99 и 0,999. Если мы задаемся, к примеру, вероятностью 0,95, значит, мы будем использовать первый столбец таблицы. Для того чтобы найти в этом столбце нужное нам число, надо найти строку, которая начинается с числа равного n-1, где n – число измерений. В нашем случае n=20, значит, мы ищем строку, начинающуюся с 19. На пересечении выбранного столбца и нужной строки и стоит нужное нам значение. В нашем случае это число равно 2,093. Следовательно, доверительный интервал будет (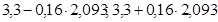) или, после вычислений (2,965; 3,635). Итак, истинное среднее (математическое ожидание) с вероятностью 0,95 лежит ГДЕ-ТО между этими двумя числами. Мы написали слово «где-то», чтобы проиллюстрировать одно из свойств доверительных интервалов: любое значение внутри интервала может оказаться математическим ожиданием с одинаковой вероятностью. Второе свойство состоит в том, что мы строили интервал с вероятностью 0,95, это означает, что с этой вероятностью истинное среднее лежит внутри интервала, но это также означает, что с вероятностью 0,05 его нет в данном интервале. Здесь мы впервые сталкиваемся с фундаментальным свойством любого статистического вывода: всегда есть вероятность, что он не верен. Статистический вывод это расчет вероятности справедливости двух гипотез: нулевой и альтернативной. Нулевая гипотеза всегда говорит «нет». Нет различий в описательных статистиках между двумя выборками, нет связи между двумя выборками и т.д. Очевидно, что альтернативная соответственно говорит «да». Возникает вопрос, когда можно считать нулевую гипотезу опровергнутой и принять альтернативную? Для этого нужно задаться уровнем значимости. Уровень значимости - это максимально приемлемая для исследователя вероятность ошибочно отклонить нулевую гипотезу, когда на самом деле она верна. В медицине принят минимальный уровень значимости 0,05. Что это значит? Если в результате расчетов мы получаем что вероятность справедливости нулевой гипотезы меньше 0,05 мы имеем право ее опровергнуть и принять альтернативную гипотезу, тем самым считать доказанным, что различия (а, следовательно, и эффект) есть.

Теперь у нас есть все необходимые понятия, для решения задачи «есть эффект или нет». Пусть мы имеем группу мужчин из 20 больных гипертонией одинакового возрастного диапазона и одинаковой тяжести заболевания. Пусть, далее они принимают новый препарат для снижения артериального давления. Необходимо ответить на вопрос: действительно ли данный препарат эффективен. Проведено фоновое (до лечения) суточное мониторированние систолического артериального давления и получены среднесуточные значения для каждого из 20 человек. После применения схемы лечения, опять проведено суточное мониторированние систолического артериального давления и также получены среднесуточные значения для каждого больного. В результате получены значения представленные в Таблице 2.

Таблица 2

Среднесуточные значения систолического артериального давления до и после лечения

Номер больного	Среднесуточное систолическое давление (до лечения), мм.рт.ст.	Среднесуточное систолическое давление (после лечения) мм.рт.ст.	Разность систолического давления до лечения и после лечения, мм.рт.ст.
			+10
			+10
			-2
			+11
			+8
			+1
			+4
			+9
			+8
			+17
			+9
			+17
			+11
			+11
			+27
			+11
			+22
			-1
			+15
			+21
	177,1	166.2	11,0
s	6,8	8,4	7,5
m	1,5	1,9	1,7

 

Алгоритм решения задачи с помощью доверительных интервалов.

1. С помощью формул (3), (4) и (10) найдем соответственно среднее арифметическое, среднеквадратичное отклонение и ошибку среднего (, s, m).
2. Построим доверительные интервалы для значений систолического давления до и после лечения. Для этого возьмем из таблицы приложения 4 (таблица распределения Стьюдента) значение для доверительной вероятности 0,95 и числа степеней свободы 19 (20-1). Это значение равно t = 2,086.
3. Сопоставим доверительные интервалы. Наименьшее значение первого интервала равно: 177,1-3,1 = 174,0, наибольшее значение второго интервала равно: 166,2+4,0 = 170,2. Интервалы не перекрываются!! Следовательно, на уровне значимости 0,05 среднее арифметическое до лечения отличается от среднего арифметического после лечения. Следовательно, лечение новым препаратом действительно эффективно.

Таким образом, можно решить Задачу 2 с помощью построения доверительных интервалов. Однако более часто используется другой подход для решения этой задачи. Он построен на вычислении экспериментального значения распределения Стьюдента и сравнения его с табличным.

Для построения этого алгоритма решения задачи 2 надо ввести еще два понятия. Зададимся вопросом можно ли в таблице 2 переставлять экспериментальные данные в столбцах произвольным порядком? Ответ: конечно нет, ведь в таком случае данные, полученные на одном пациенте попадут к другому! Такие выборки называются связанными выборками. В нашем случае они связаны номером пациента. Для таких выборок экспериментальное значение распределения Стьюдента рассчитывается по формуле:

(13)

В формуле (13) - среднее арифметическое разности, - среднеквадратичное отклонение для разности, - ошибка среднего для разности. Используя значения в таблице 2, рассчитаем .

Как мы уже знаем, табличное значение () для уровня 0,95 и числа степеней свободы 19 (20-1) равно 2,086, следовательно, в нашем случае . Следовательно, наблюдаемые различия в артериальном давлении действительно существуют. В настоящий момент мы делаем этот вывод на уровне значимости 0,05. Но теперь, когда мы имеем экспериментальное значение распределения Стьюдента, мы можем его сравнить с табличными значениями для других доверительных вероятностей. Посмотрим, например, чему равно табличное значение распределения Стьюдента для доверительной вероятности 0,99 (уровень значимости 0,01). Как следует из таблицы приложения 4, это значение равно 2,861, а для доверительной вероятности 0,999 (уровень значимости 0,001) – 3,883. Поскольку 6,47 > 3,883, мы можем сделать вывод о том, что изучаемое лекарство эффективно не только на уровне 0,05, т.е. допуская что вероятность ошибки не больше 5%, но и на уровне 0,001, т.е. вероятность того, что наш вывод не верен не превышает 0,1%!!!

Приведенные выше расчеты справедливы для связанных выборок. Теперь будем решать ту же задачу (действительно ли есть эффект или полученные различия есть не более чем игра случая) для не связанных выборок.

Рассмотрим, как проверяется гипотеза о неравенстве средних для несвязанных выборок. В этом случае экспериментальное значение распределения Стьюдента можно рассчитать по формуле:

(14)

В формуле (14) и соответственно среднее арифметическое для первой выборки и среднее арифметическое для второй выборки. Аналогично - объем первой выборки, - объем второй выборки, s – объединенная оценка среднеквадратичного отклонения двух групп, которая вычисляется по формуле: (15)

В формуле (15) - оценка среднеквадратичного отклонения для первой группы, а - для второй. - значение распределения Стьюдента, рассчитанное по экспериментальным данным.

В таблице 3 приведены значения усредненной по всем оценкам успеваемости двух групп студентов в первом семестре. Необходимо определить, можно ли считать, что одна группа училась лучше другой.

Очевидно, что в данном случае мы имеем дело с несвязанными выборками.

Таблица 3

Осредненная успеваемость студентов двух групп за первый семестр.

№ по порядку	Успеваемость в первой группе (средний балл за семестр)	Успеваемость во второй группе (средний балл за семестр)
	4,1	3,1
	3,8	3,7
	4,1	3,8
	3,5	3,2
	3,2	4,0
	2,9	3,4
	3,7	3,6
	4,2	4,1
	5,0	3,3
	2,8	4,2
	3,6	2,7
	4,9	3,2
		2,7
		3,9
N
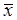
	3,82	3,49
s по группам	0,69	0,49
s объединенное среднеквадратичное отклонение	0,59

 

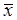- рассчитывали по формуле (3), и рассчитывали по формуле (4). Используя формулу (15) рассчитаем s:

 

Теперь используя формулу (14) рассчитаем экспериментальное значение распределения Стьюдента:

Далее находим теоретическое значение распределения Стьюдента для доверительной вероятности 0,95 и числом степеней свободы . То есть, ищем число, стоящее на пересечении первого столбца таблицы Приложения 4 и 24 строки. Из таблицы следует, что это число равно .

Следовательно, в нашем случае: 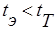, и мы не имеем права говорить, что одна группа учиться лучше (или хуже) другой. Мы вынуждены признать, что различия, наблюдаемые в успеваемости групп, носят случайный характер, а в целом успеваемость в группах одинакова.

Этим заканчивается решение задачи 2. Осталось сделать только два замечания.

Замечание 1 состоит в том, что приведенные выше схемы расчетов справедливы в том случае, если обе выборки сделаны из генеральных совокупностей, распределенных по закону Гаусса.

Замечание 2. Мы отдаем себе отчет в том, что в настоящее время никто в реальных расчетах считать вручную не будет. Однако для закрепления материала очень полезно провести расчеты с использованием калькулятора. Для этих целей ниже приводится полное решение модельной задачи.

Задача Содержание свободного гепарина крови в двух различных возрастных группах принимало следующие значения:

 

X1(мг%)	5,7	5,9	6,3	5,6	4,1	4,0	4,5	5,0	5,1	6,7
X2(мг%)	5,1	3,2	6,0	5,1	4,9	3,8	6,2	4,5	5,6	5,8

 

1. Вычислить выборочную среднюю арифметическую, среднеквадратичное отклонение, стандартную ошибку среднего, медиану, коэффициент вариации для каждого ряда и доверительные интервалы для средних. Сравнить средние значения гепарина для двух возрастных групп.

Решение:

Число измерений в каждом ряду n=10.

Выборочная средняя определяется по формуле:

Следовательно для первого ряда она равна:

 

Найдем дисперсию по формуле:

Следовательно, для первого ряда выборочная дисперсия равна:

Вычислим среднеквадратичное отклонение .

Вычислим стандартную ошибку среднего

Для определения медианы (Ме₁) по заданным значениям х_1i строим вариационный ряд:

4,0 4,1 4,5 5,0 5,1 5,6 5,7 5,9 6,3 6,7

 

При четном числе вариант медиана определится как среднее арифметическое из двух центральных вариант:

(мг,%)

Вычислим коэффициент вариации .

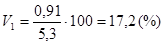
Рссчитаем 95% доверительный интервал для среднего. В нашем случае число измерений 10, а доверительная вероятность 0,95. Входим в таблицу приложения 4. На пересечении столбца 0,95 и девятой строки стоит число t= 2,262.

Следовательно, в нашем случае, , и значит доверительный интервал будет или окончательно .

Проведя аналогичные расчеты для второго ряда получим:

Сравнивая доверительный интервал для среднего первого ряда, с доверительным интервалом для второго ряда, легко увидеть, что они сильно перекрываются. Следовательно, наблюдаемые различия между средними являются случайными и мы должны прийти к заключению, что различий между ними нет.

2. Сравнить средние, используя вычисление экспериментального значения распределения Стьюдента.

В данном случае мы имеем дело с не связанными выборками, поэтому для вычисление экспериментального значения будем использовать следующую формулу: .

Вычислим объединенная оценка среднеквадратичного отклонения двух групп:

Тогда 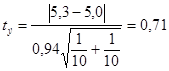. Число степеней свободы в нашем случае равно n=10+10-2=18. Итак, входим в таблицы Приложения 4 по восемнадцатой строке и первому столбцу. На пересечении стоит число 2,103. Это число намного больше, чем полученное 0,71. Следовательно, мы приходим к тому же заключению, что средние двух выборок не различаются.

Итак, ответ в данном случае, будет выглядеть так: 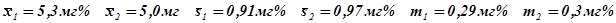.
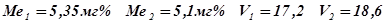