Задача 1. Рассчитать коэффициент парной линейной корреляционной зависимости, сделать вывод по знаку коэффициента корреляции и о степени связи следующих величин.
| Объем крови х i (л) | 4,22 | 4,69 | 5,04 | 4,34 | 4,22 | 4,8 | 4,45 | 4,69 | 4,92 | 4,57 |
| Вес у i, (кг) |
Решение. Определим выборочные средние:
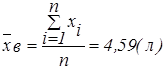
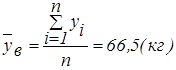
Составим таблицу:
| S | |||||||||||
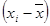 (л) (л)
| -0,37 | 0,1 | 0,45 | -0,25 | -0,37 | 0,21 | -0,14 | 0,1 | 0,33 | -0,02 | |
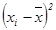 (л2) (л2)
| 0,14 | 0,01 | 0,20 | 0,06 | 0,14 | 0,04 | 0,02 | 0,01 | 0,11 | 0,0004 | 0,73 |
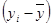 (кг) (кг)
| -14,5 | 6,5 | 19,5 | -12,5 | -16,5 | 7,5 | -5,5 | 2,5 | 13,5 | -0,5 | |
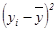 (кг2) (кг2)
| 210,25 | 42,25 | 380,25 | 156,25 | 272,25 | 56,25 | 30,25 | 6,25 | 182,25 | 0,25 | 1336,5 |
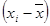 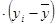 (л,кг) (л,кг)
| 5,36 | 0,65 | 8,77 | 3,125 | 6,10 | 1,57 | 0,77 | 0,25 | 4,45 | 0,01 | 31,05 |
Вычислим выборочные среднеквадратические отклонения:
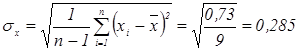 (л)
(л)
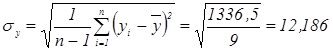 (кг)
(кг)
Вычислим оценку ковариации:
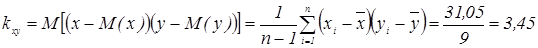 (л, кг)
(л, кг)
Вычислим коэффициент корреляции:
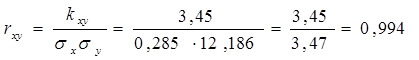
Вывод: С увеличением веса человека объем циркулирующей крови увеличивается, причем связь между этими параметрами является сильной.
Задача 2. Рассчитать коэффициент парной корреляционной зависимости, сделать вывод по знаку коэффициента корреляции, о степени связи между величинами, построить корреляционное поле и провести линию регрессии:
| Основной обмен веществ хi (%) | ||||||||||
| Амплитуда артериального давление уi (мм рт.ст.) |
Решение
Вычислим выборочные средние  и
и 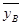 :
:
 =
= 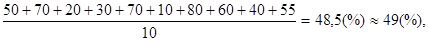
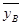 =
= 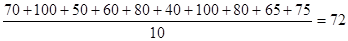 (мм рт.ст)
(мм рт.ст)
Заполним таблицу:
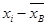 (%) (%)
| -29 | -19 | -39 | -9 | ||||||||
 (%)2 (%)2
| 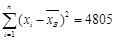
| |||||||||||
 (мм рт.ст.) (мм рт.ст.)
| -2 | -22 | -12 | -32 | -7 | |||||||
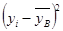 (мм рт.ст.)2 (мм рт.ст.)2
| 
| |||||||||||
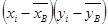 (%, мм рт.ст.)
(%, мм рт.ст.)
| -2 | 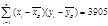
|
Вычислим выборочные средние квадратичные отклонения σх и σу:
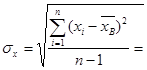
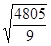 =
= 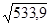 =23,11(%),
=23,11(%),

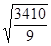 =
= 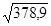 ≈19,47 (мм.рт.ст)
≈19,47 (мм.рт.ст)
Вычислим оценку ковариации kх,у:
kх,у 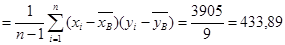
Вычисляем коэффициент корреляции rx,y:
rx,y= 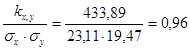
Построим корреляционное поле и проведем линию регрессии:
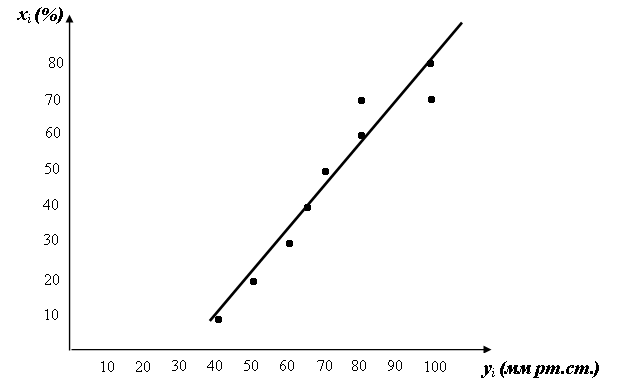
Вывод: Связь между основным обменом веществ (%) и амплитудой артериального давления (мм рт. ст) очень тесная, так как, rx,y>0,7 и с увеличением основного обмена амплитуда артериального давления растет (почти прямо пропорциональная зависимость, так как rx,y ≈1).
Задача 2. Рассчитать коэффициент корреляции при атеросклерозе между площадью поражений артерий таза (%) и возрастом больного. Сделать вывод о связи исследуемых величин.
| n=8 | |||||||||
| х (%) | 22,3 | 3,1 | 48,3 | 17,0 | 7,5 | 40,2 | 23,1 | 16,0 | 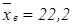
|
| у (годы) | 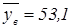
| ||||||||
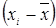 (%) (%)
| 0,1 | -1,91 | 26,1 | -5,2 | -14,7 | 0,9 | -6,2 | ||
 (%)2 (%)2
| 0,01 | 364,8 | 681,2 | 216,1 | 0,81 | 38,4 | ∑=1652,3 | ||
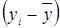 (год) (год)
| 1,9 | -21,1 | 21,9 | -3,1 | -8,1 | 11,9 | 1,9 | -8,1 | |
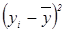 (год)2 (год)2
| 3,6 | 445,2 | 4,796 | 9,6 | 65,6 | 141,6 | 3,6 | 65,6 | ∑=1214,4 |
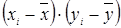 (%, год) (%, год)
| 0,2 | 571,6 | 16,1 | 119,1 | 214,2 | 1,71 | 50,2 | ∑=1376,1 |
Вычислим выборочные среднеквадратические отклонения:
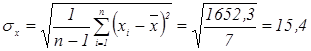 (%),
(%),
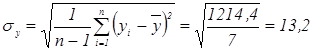 (год).
(год).
Вычислим оценку ковариации:
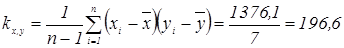 (%, год).
(%, год).
Вычислим коэффициент корреляции:
 .
.
Вывод: С увеличением возраста больного атеросклерозом площадь поражений артерий таза увеличивается. Связь между этими параметрами является сильной.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задачи для домашнего решения
Рассчитать коэффициент парной линейной корреляционной зависимости, сделать вывод по знаку коэффициента корреляции и о степени связи между следующими величинами
а)
| Амплитуда вызванных потенциалов мозга (мкВ) | 2,3 | 4,0 | 7,4 | 4,5 | 6,7 | 10,0 | 9,2 | 10,8 | 8,3 | 15,2 |
| Латентный период (мс) | 15,7 | 20,6 | 25,6 | 34,6 | 48,5 | 66,6 | 96,1 | 127,2 | 73,5 | 178,4 |
б)
| Вес щитовидной железы (г) | ||||||||||
| Площадь стеннографического изображения (см2) |






