Почему при решении предыдущих задач ничего не говорилось о системе отсчета? Выходит, можно обойтись без этого понятия? Нет. Когда речь идет о перемещении, скорости, ускорении обязательно имеется в виду какая-то система отсчета. Правда, она часто не называется, если является привычной, для всех очевидной. Когда водителя автомобиля штрафуют за превышение скорости, всем ясно, что имеется в виду скорость относительно дороги, а не относительно встречной машины.
При решении некоторых физических задач необходимо явно указывать систему отсчета, а иногда и переходить от одной системы отсчета к другой.
Задача 10. 1*. Оцените, на сколько дальше спортсмен бросит гранату, если будет бросать ее с разбега.?
Что дано? Что нужно найти? Как кратко записать условие? Не простые вопросы в данном случае. Жизнь не добрая учительница, которая четко дает ясные задания. Часто приходится самостоятельно формулировать и уточнять саму задачу.
Еще раз прочитайте условие. Обратите внимание на слово «оцените». Это означает, что нужно решить задачу в грубом приближении, учтя лишь самое существенное, проводя вычисления с точностью до одной-двух значащих цифр. Представьте себе, что описываемая в задаче ситуация относится лично к вам. Какие характеризующие вас данные могут понадобиться при решении задачи?
Прежде всего, видимо, придется использовать некоторые ваши спортивные достижения.
Как далеко вы можете бросить гранату с места? Если очень постараться, то метров на 40 – 50. Примем, что дальность бросания без разбега
S0 = 50 м.
Ясно, что чем быстрее будет разбег, тем более дальним бросок. Как быстро вы бегаете на короткие дистанции? Видимо, стометровку сможете пробежать за 11 – 12 секунд. Поэтому примем скорость разбега равной
u = 100 / 12» 8 (м /с).
От чего еще может зависеть дальность броска? Наверно как-то влияет и рост спортсмена, и направление ветра. Однако при оценках можно пренебречь этими факторами и рассматривать движение частицы с постоянным ускорением, равным ускорению свободного падения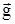 
, между точками, лежащими на горизонтальной поверхности земли. Частица брошена под некоторым углом a к горизонту так, что дальность полета S оказалась максимальной.
Как видим, этап У словие общего плана решения в некоторых случаях предполагает уточнение и дополнение самой задачи.
Теперь можно и кратко записать условие.
На рисунке 10 показаны: траектория полета, скорость разбега 
, начальная скорость гранаты 
и угол a, определяющий ее направление, перемещение 
, модуль которого представляет собой дальность броска, ускорение свободного падения 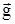. Подразумевается, что все эти величины заданы в системе отсчета «Земля».
А нализ содержания задачи предполагает, в частности, выяснение качественно причины описываемого явления. Почему же разбег увеличивает дальность броска? Говорят, что за счет разбега увеличивается начальная скорость гранаты. Почему? Какой физический закон ответственен за это? Поскольку речь идет о добавке к скорости, вероятно, тут дело не обходится без закона сложения скоростей. Конечно. А еще какие законы придется применять? Так как речь идет о движении частицы с постоянным ускорением (
), здесь применимы соотношения (4.6) – (4.8).
Как при помощи указанных законов получить необходимую систему У равнений? Нельзя ли и здесь воспользоваться принципом «разделяй и властвуй»? Естественно. Ведь нужно сравнивать результаты двух подзадач: бросок с места и бросок с разбега. Во втором случае можно выделить еще одну подзадачу – о нахождении скорости движения гранаты относительно земли. = ГЗ.
Будем реализовывать намеченный план получения необходимых уравнений.
Для первой подзадачи, применяя формулу (4.6), нетрудно получить (проделайте самостоятельно) соотношение, связывающее дальность полета S0 с начальной скоростью v0, направленной под углом a к горизонту:
S0 = 
sin 2a. (10.1)
Максимальное S0 при данном v0 получается при a0 = 450. Оно равно
S0 = v02 / g. (10.2)
Переходим ко второй подзадаче. По аналогии с первой запишем кинематическое уравнение (4.6) для перемещения в проекции на оси x и y (рис. 10):
S = vX t, (10.3)
0 = vY t – g t2 / 2. (10.4)
Какой смысл имеют входящие в эти уравнения величины vX и vY? Это проекции на оси x и y начальной скорости движения гранаты относительно земли. Нельзя ли vX и vY связать с величиной v0, фигурирующей в формулах (10.1) и (10.2)? Под v0 можно понимать модуль скорости гранаты относительно спортсмена. (vГС = v0). Только сила и сноровка спортсмена определяют эту величину. Так что она не меняется при переходе ко второй подзадаче. Как же, зная эту величину, найти vX и vY? Для этого нужно применить закон сложения скоростей (3.4):
= ГЗ = ГС + СЗ = ГС + . (10.6)
Это равенство иллюстрируется векторным треугольником на рисунке 10.
Модуль вектора ГС известен (vГС = v0), а направление (угол b) – нет. Как выразить входящие в (10.3) и (10.4) проекции вектора ? Для это нужно спроецировать равенство (10.6) на оси x и y:
vX = v0 cos b + u, (10.7)
vY = v0 sin b. (10.8)
Получилась система уравнений (10.3), (10.4), (10.7), (10.8), из которой нужно найти величину S. Решите эту систему самостоятельно. Получится
S = u 
sin b + sin (2b), или, после подстановки (10.2), –
S = S0 (sin (2b) +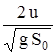 
sin b). (10.9)
Для обеспечения максимальной величины S следовало бы еще определенным образом подобрать угол b. Проще всего такой отбор провести с помощью ЭВМ. Однако для оценок можно считать, что спортсмен по привычке бросает гранату под одним и тем же углом, не зависимо от скорости разбега, то есть. b» p / 4. Тогда формула (10.9) упрощается:
S – S0» 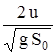sin (p/4) = u 
. (10.10)
Проверьте наименование полученного ответа и подсчитайте численное значение. Должно получиться S – S0» 2×101 м, то есть разбег может увеличить результат приблизительно в 1,5 раза. В справедливости такого заключения вы можете убедиться на собственном спортивном опыте. Дерзайте!
Компьютерный анализ более точной формулы (10.9) показывает, что функция S(b) принимает максимальное значение, равное 69 м при b = 500. Это существенно не отличается от найденного по упрощенной формуле (10.10) оценочного результата.
В копилку опыта
· Условие физической задачи, возможно, нуждается в уточнении, дополнении, упрощении.
· От привычной системы отсчета («Земля») иногда целесообразно перейти к иной («Бегущий спортсмен»).
· Закон сложения скоростей полезно представлять в форме векторного треугольника.
· В некоторых задачах целесообразно записывать закон сложения скоростей в проекциях.
· Оценочный характер задачи позволяет упрощать полученные уравнения. В данном случае уравнение (10.9) сводится к (10.10) посредством приближенного равенства b» a0 = p / 4.
Задача 10. 2*. Из двух точек, находящихся на горизонтальной поверхности на расстоянии 10 м друг от друга, одновременно бросили два тела со скоростями 1 и 2, направленными под углами a1 = 300 и a2 = 600 к горизонту, соответственно. Скорости 1 и 2 таковы, что тела при падении меняются местами. Определить скорость одного тела относительно другого в тот момент, когда оба тела находятся на одной вертикали.
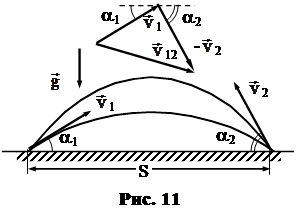Анализируя содержание задачи, можно обнаружить знакомую подзадачу о движении частицы с постоянным ускорением свободного падения , брошенной под углом к горизонту. Из решенияч этой подзадачи следует, что рассматриваемые здесь тела движутся по параболическим траекториям, изображенным на рисунке 11, и справедливо (получите самостоятельно) записанное ниже соотношение, определяющее дальность полета S1 первого тела, брошенного с начальной скоростью v1 под углом a1 к горизонту:
S1 = 
. (10.11)
Аналогичное соотношение имеет место и для второго тела:
S2 = 
. (10.12)
По условию задачи S1 = S2 = S.
Эти уравнения характеризуют описываемую в задаче физическую ситуацию, но в них не входит искомая величина v12. Какой закон нужно применить для нахождения скорости 12 движения первого тела относительно второго? Чтобы связать 12 с 1 и 2, нужно применить закон сложения скоростей (3.4):
12 = 1З + З2 = 1З – 2З. (10.13)
Здесь 1З = 1(t) – скорость первого тела относительно земли, а 2З = 2(t) – скорость второго тела относительно земли, отличающаяся только знаком от скорости земли относительно второго тела ( З2). Соотношение (10.13) справедливо для произвольного момента времени t. На рисунке 11 изображен векторный треугольник, определяющий скорость 12 в начальный момент времени.
Как изменяется вектор 12 с течением времени? Какая величина характеризует изменение скорости? Изменение скорости 12 определяется ускорением 
12 первого тела относительно второго. Из какого закона можно найти это ускорение? Ускорение 
12 можно связать с ускорениями каждого из тел с помощью закона сложения ускорений:
12 = 1З + З2 = 1З – 2З = – = 0.
Благодаря тому, что оба тела движутся относительно земли с одинаковыми ускорениями (), друг относительно друга они движутся равномерно и прямолинейно. Так что искомая в задаче скорость равна скорости 12 в начальный момент времени, которая определяется изображенным на рисунке 11 векторным треугольником.
При заданных в задаче углах a1 и a2 треугольник оказывается прямоугольным (докажите это самостоятельно). Поэтому v12 находится по теореме Пифагора с учетом соотношений (10.11) и (10.12):
V12 = 
= 
= 
»15 м/с.
В копилку опыта
· 
Переход в другую систему отсчета иногда упрощает задачу. В данном случае движение первого тела относительно второго оказалось равномерным и прямолинейным.
· Характер движения в новой системе отсчета выясняется посредством закона сложения ускорений.
· Для нахождение величин, фигурирующих в законе сложения скоростей, часто удобнее оказывается геометрический метод, а не метод записи векторных уравнений в проекциях на координатные оси.
Задача 10. 3*. Скорость воды в реке равна u, а скорость пловца – v. Под каким углом к скорости должен плыть пловец, переплывающий реку, чтобы его снос по течению оказался минимальным?
На рисунке 12 изображены скорости и , а также перемещение ПБ пловца относительно берега. Этому перемещению соответствует снос S.
А нализ содержания задачи приводит к заключению, что следует применить закон сложения скоростей (3.5) для нахождения скорости пловца относительно берега ( ПБ) и обеспечить наименьшее значение угла b, образованного этой скоростью и перпендикуляром к берегу.
Применим закон (3.5):
ПБ = ПВ + ВБ = + = + . (10.14)
Опыт решения предыдущих задач подсказывает, что нужно строить векторный треугольник, соответствующий равенству (10.14). Начнем с заданного вектора (рис. 13). Второе слагаемое известно лишь по модулю. Поэтому ясно, что конец вектора должен находиться где-то на окружности, изображенной на рисунке 13. В зависимости от угла a это могут быть точки A1, A2, A3, и т. д. Вектор ПБ и, следовательно, угла b (рис.13) определяются положением конца вектора .
Где же должен находиться конец вектора , для того, чтобы угол b оказался минимальным? Из рисунка 13 видно, что для этого направленный отрезок должен оканчиваться в точке A, так чтобы угол b оказался равным нулю. Какой вид тогда принимает треугольник скоростей? Он оказывается прямоугольным. Какие элементы этого треугольника известны? Его катет равен u, а гипотенуза – v. Какое отношение к нему имеет искомый угол a? Он является внешним углом этого треугольника. Как же его можно найти? Как сумму внутренних углов, не смежных с ним:
a = p / 2 + g, где sin(g) = u /v.
Итак, a = p / 2+ arcsin (u / v). (10.15)
А нализ результата.
Ответ (10.15) имеет смысл только при условии u < v. При u = v угол a = p, чего не может быть для пловца, переплывающего реку. Соотношение u < v случайно оказалось в основе построений, выполненных на рисунке 13. Нужно проанализировать альтернативный вариант.
Проделаем построения, аналогичные прежним, но предполагая, что
u > v (рис. 14).
Где теперь должен находиться конец вектора , для того, чтобы угол b оказался минимальным? Как меняется этот угол при переходе от точки A1 к точкам A2, A3? Как найти точку A, соответствующую наименьшему углу b? Для ответа на последний вопрос следует провести касательную к окружности из начала вектора . Какой вид принимает треугольник скоростей, соответствующий минимальному углу b? Он оказывается прямоугольным, причем u – его гипотенуза, v – катет, а a – внешний угол. Как же найти этот угол? Поступаем аналогично тому, как это делалось в рассмотренном ранее варианте. Получаем
a = p / 2+ arcsin (v / u).
Общий ответ можно записать так:
|
p / 2+ arcsin (v / u), если u > v.
В копилку опыта
· Снова при применении закона сложения скоростей полезным оказался геометрический метод. Помогли дополнительные построения: проведение окружности, касательной к ней.
· Анализ результата в данной задаче выявил область применимости полученного ответа и привел к новой задаче: исследовать явление при иных соотношениях между заданными величинами. Формулировка новой задачи на основе анализа результата – типичный путь развития научных исследований.
