Персональную тройку» – каждому

Задача 17. 1. Два бруска, массы которых m₁ и m₂, связаны нитью и находятся на поверхности стола. К одному из брусков приложена сила , направленная в сторону, противоположную нити. Найти силу ее натяжения, если коэффициент трения брусков о поверхность стола равен m, нить в начальный момент практически не провисает, а брусок находится в покое.

Поскольку речь идет о нахождении сил, задача относится к компетенции динамики. Но законы Ньютона формулируются для частицы, а рассматриваемую в задаче систему, вообще говоря, нельзя считать частицей. Как быть? Следуя принципу «разделяй и властвуй», можно отдельно анализировать движение каждого бруска и нити. Тогда задача распадается на три задачи о движении

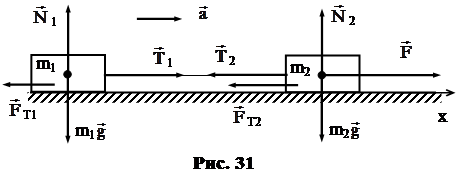частиц (и бруски, и нить движутся поступательно). Для каждой из частиц можно «запрячь персональную тройку» законов Ньютона.

В качестве инерциальной системы отсчета естественно принять «Лабораторию», неподвижную относительно Земли. Для записи уравнений второго закона Ньютона в этой системе отсчета, следует, по крайней мере, указать направление ускорений рассматриваемых частиц. Что по этому поводу можно почерпнуть из условия задачи? Ясно, что ускорение всех трех тел может быть направлено так, как показано на рисунке 31, то есть в сторону приложенной силы . А может ли это ускорение быть равным нулю? Может, если модуль силы слишком мал. При решении задач с абстрактным содержанием (без конкретных чисел) следует учитывать все возможные варианты. Каковы же они в данной задаче?

Сила может быть столь мала по модулю, что не в состоянии сдвинуть с места брусок m₂ и, следовательно, натянуть нить, то есть

T₁ = T₂ = T = 0. (17.1)

Такая ситуация возникнет при условии

F = F_Т2 £ m m₂ g, (17.2)

где _T2 – сила трения, действующая на брусок m₂ (рис.31). Эта сила удовлетворяет условию (13.8), поскольку является в данном случае силой трения покоя.

Если модуль силы превысит ограничение (17.2), то нить натянется, и может возникнуть ускорение . Оно одинаково для всех частей системы, поскольку деформация нити пренебрежимо мала – «нить нерастяжима».

Запишем в проекциях на ось x уравнение второго закона Ньютона для бруска m₁ (рис. 31):

m₁ a = T₁ – F_Т1. (17.3)

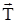₁ – сила натяжения нити, приложенная к первому бруску, а _Т1 – сила трения, удовлетворяющая условию

F_Т1 £ m m₁ g. (17.4)

Знак «<» в (17.4) относится только к частному случаю a = 0 (сила трения покоя), знак «=» помимо этого описывает и движение с a ¹ 0 (сила трения скольжения).

Аналогичным образом для второго бруска получим

m₂ a = F – T₂ – F_Т2. (17.5)

Здесь сила F_Т2 принимает свое максимально возможное значение, равное силе трения скольжения

F_Т2 = m m₂ g. (17.6)

Запишем в проекциях на ось x уравнение второго закона Ньютона для нити, полагая, что ее масса равна m_Н. Силы, приложенные к нити со стороны брусков (на рис. 31 не показаны), отличаются лишь знаком от сил 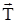₁ и 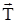₂ в соответствии с третьим законом Ньютона. Получим

m_Н a = T₂ – Т₁. (17.7)

В связи с тем, что масса нити m_Н много меньше массы брусков m₁ и m₂, а T₁ и T₂, как видно из формул (17.3) и (17.5), порядка m₁a и m₂a, величиной m_Н a в формуле (17.7) можно пренебречь по сравнения с T₁ и T₂, то есть положить

T₁» T₂» T. (17.8)

Это часто используемое приближение означает, что «невесомая» нить передает силу натяжения от одной ее точки к другой без изменения.

Складываем уравнения (17.3) и (17.5) после подстановки в них (17.6) и (17.8):

(m₁ + m₂) a =F – F_Т1 – m m₂ g. (17.9)

Если a = 0, то из (17.9), (17.3) и (17.8) получаем

T = F – m m₂ g. (17.10)

Этот результат справедлив за рамками ограничения (17.2), но при условии (17.4), которое после подстановки (17.10) принимает вид

F_Т1 = T = F –– m m₂ g £ m m₁ g Þ F £ m (m₁ + m₂) g. (17.11)

Если a ¹ 0, то величину F_Т1 следует выразить из равенства (17.4) и подставить в (17.9) Тогда

a = F / (m₁ + m₂) – m g.

Это выражение совместно с (17.3) и (17.8) позволяет получить

T = F m₁ / (m₁ + m₂). (17.12)

Найденный результат справедлив за рамками ограничения (17.11).

Объединяя полученные соотношения (17.1), (17.10) и (17.12), а также соответствующие им условия (17.2) и (17.11), можно записать ответ в компактном виде:

0, если F = £ m m₂ g;

T = F – m m₂ g, если m m₂ g £ F £ m (m₁ + m₂) g;

F m₁ / (m₁ + m₂), если F ³ m (m₁ + m₂) g.

Один из элементов А нализа результата заключается в проверке равенства значений T, даваемых разными строками этого выражения, на границе соответствующих областей.

В копилку опыта

· Если система состоит из нескольких частиц, то для каждой из них приходится «запрягать персональную тройку» законов Ньютона.

· Невесомая нить передает без изменения силу натяжения от одной ее точки к другой.

· Иногда ответ представляет собой не одно равенство, а совокупность нескольких выражений, включающих и неравенства.

Задача 17. 2. Найти ускорения грузов и силы натяжения нитей в системе, показанной на рисунке 32. Блоки считать идеальными и невесомыми, нити – нерастяжимыми.

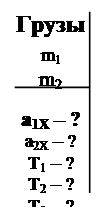Ускорения грузов ₁ и ₂ могут быть направлены или так, как показано на рисунке 32 сплошной стрелкой, или в противоположном направлении (пунктирная стрелка). Чтобы не анализировать оба варианта по отдельности, введем ось x (рис. 32) и будем искать проекции ускорений a_1X и a_2X.

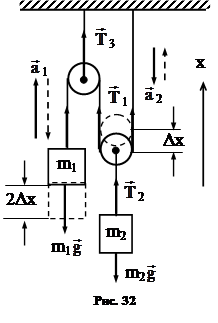
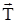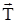Модули сил натяжения ₁, ₂ и 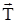₃ нужно найти для каждой из трех нитей (рис. 32). О каких именно точках нитей здесь идет речь, не имеет значения, поскольку нити невесомы и блоки идеальны. Идеальные блоки не обладают массой и могут свободно поворачиваться, в результате чего они не меняют сил натяжения охватывающих их нитей.

Какие законы нужно применить для решения этой задачи? Нужно применить законы Ньютона для каждой из частиц, которыми можно считать грузы и блоки. Массу блоков при этом полагаем сосредоточенной в их центре масс.

В качестве инерциальной системы отсчета возьмем лабораторию, неподвижную относительно Земли. Именно в этой системе отсчета нужно находить ускорения ₁ и ₂.

Запишем в проекциях на ось x (рис. 32) уравнения второго закона Ньютона для грузов m₁ и m₂:

m₁ a_1X = T₁ – m₁ g, (17.13)

m₂ a_2X = T₂ – m₂ g, (17.14)

Здесь m₁ и m₂ – силы тяжести грузов, а 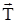₁, и 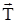₂ – силы натяжения нитей (рис. 32)

Достаточно ли этих уравнений для решения задачи? Какие еще соотношения можно использовать? Можно применить уравнения второго закона Ньютона для блоков:

0 = T₃ – 2 T₁, (17.15)

0 = 2 T₁ – T₂. (17.16)

Хотя ускорение второго блока отлично от нуля, нулю равны левые части обоих уравнений, поскольку идеальные блоки невесомы. Сила, действующая на первый блок со стороны огибающей его нити, равна – 2 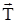₁. Она только знаком отличается от силы, действующей со стороны той же нити на второй блок (рис. 32).

Нужны ли еще какие-либо уравнения для решения задачи? В полученные четыре уравнения входят пять неизвестных: a_1X, a_2X, T₁, T₂ T₃, так что необходимо составить еще одно уравнение, в которое входили бы величины a_1X и a_2X. Все ли учтено из того, что задано в условии задачи? Пока никак не учитывалось, что нить нерастяжима. Именно это свойство нити и позволяет связать величины a_1X, a_2X. Чтобы поднять подвижный блок на высоту Dx, следует опустить левый конец нити на 2 Dx (рис. 32). Поэтому скорость и ускорение груза m₁ по модулю оказываются вдвое больше по сравнению с этими величинами для груза m₂. Так находим

a_1X = – 2 a_2X. (17.17)

Осталось решить полученную систему уравнений. Проделайте это самостоятельно и сравните с приведенными здесь ответами:

a_1X = 2 g 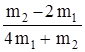; a_2X = g 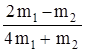; T₁ = 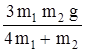; T₂ = T₃ = 2 T₁.

Проводя А нализ результата, следует, в частности, рассмотреть условие равновесия, а также выяснить направление возникающих при его нарушении ускорений. При равновесии (a_1X = 0) m₂ = 2 m₁ и T₁ = m₁ g. Если m₂ > 2 m₁, то a_1X > 0, и, следовательно, ускорение ₁ направлено вверх (рис. 32, сплошная стрелка). Если же m₂ < 2 m₁, то оно направлено в противоположную сторону. В пределе при m₁ ® 0 ответы дают физически очевидные значения: a_2X = – g, a_1X = 2 g, T₁ = T₂ = T₃ = 0.

В копилку опыта

· Идеальный блок не меняет силу натяжения охватывающей его нити.

· Для идеального блока можно записывать условие равновесия даже тогда, когда ось его движется с ускорением.

· Перемещение, скорость и ускорение подвижного блокавдвое меньше по сравнению с соответствующими величинами конца охватывающей его нити.

Задача 17. 3*. На гладком горизонтальном столе находится клин массой M с углом наклона a при основании. На наклонную грань клина кладут брусок массой m, привязанный к нити. Нить перекинута через идеальный блок, укрепленный на вершине клина, и прикреплена к стене (рис. 33). Отрезок нити между стеной и блоком расположен горизонтально. Брусок начинает скользить по поверхности клина. С каким ускорением при этом движется клин?

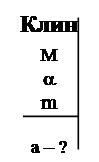Из А нализа условия следует, что нужно применить законы динамики для клина и для бруска. Инерциальная система отсчета – «Земля». Именно в этой системе отсчета предполагается находить ускорение клина (рис. 33).

Применим второй закон Ньютона для клина. Какие силы приложены к нему? M – сила тяжести; – сила реакции стола; – – сила давления бруска. На рисунке 33 показана приложенная к бруску со стороны клина сила , которая связанная с силой давления третьим законом Ньютона. Нить, опираясь на блок, также действует на клин. Сила со стороны горизонтального участка нити 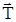направлена к стене, а с противоположной стороны к блоку приложена сила – 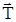₁. На рисунке 33 показана равная ей по модулю сила натяжения нити 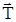₁, приложенная к бруску. Невесомая нить передает силу натяжения от точки к точке без изменения, идеальный блок лишь изменяет ее направление, так что T = T₁.

В проекциях на ось x (рис. 33) уравнение второго закона Ньютона для клина принимает вид

M a = T – T cos a + N sin a. (17.18)

Теперь следует применить второй закон Ньютона к бруску. Приложенные к нему силы показаны на рисунке 33. Что известно об ускорении бруска? Относительно клина он движется с ускорением _1К (рис. 33), направленным вдоль поверхности клина. Но в уравнение должно войти ускорение ₁ = _1З относительно инерциальной системы отсчета. Таковой является «Земля». Приходится применить закон сложения ускорений (3.5):

₁ = _1З = _1К + _КЗ = _1К + . (17.19)

Следует также учесть нерастяжимость нити, вследствие чего

a = a_1К. (17.20)

Проецируя уравнение (17.19) на координатные оси x и y (рис. 33), получим с учетом (17.20):

a_1X = – a cos a + a, (17.21)

a_1Y =a sin a. (17.22)

Уравнение второго закона Ньютона в проекциях на оси x и y для бруска принимает вид:

m a_1X = T cos a – N sin a, (17.23)

m a_1Y = m g – T sin a– N cos a. (17.24)

Из системы (17.18), (17.23), (17.21) и (17.22) можно найти (проделайте самостоятельно):

a = .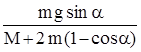

В копилку опыта

· Перейти в инерциальную систему отсчета поможет закон сложения ускорений.

· Геометрические связи частиц системы (нерастяжимые нити, неизменные углы наклона плоскостей и т. п.) позволяют получить необходимые дополнительные соотношения между ускорениями частей системы

Задачи статики

 

Задачами статики называют задачи динамики, в которых ускорения частиц равны нулю, то есть система находится в равновесии. Если система состоит из небольшого числа частиц, то достаточно записать уравнения второго закона Ньютона для этих частич, приравняв нулю ускорения. Часто приходится иметь дело с системами, состоящими из нескольких твердых тел. В этих случаях пользуются условиями равновесия абсолютно твердого тела.

Задача 18. 1. Тонкий однородный стержень укреплен на шарнире в точке A и удерживается в равновесии горизонтальной нитью (рис. 34). Масса стержня – 1,0 кг. Он наклонен к горизонту под углом 45⁰. Найти силы, с которыми стержень действует на шарнир и на нить.

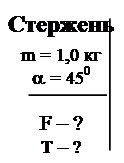А нализ предполагает, в частности, выяснение смысла используемых терминов. Что такое шарнир и куда может быть направлена сила ? Под шарниром понимают такое соединение стержня с некоторой точкой, при котором стержень может свободно поворачиваться вокруг нее. Искомые силы по третьему закону Ньютона отличаются только знаком от соответствующих сил реакций, действующих на стержень. Последние и будем находить. Направление силы реакции стержня не известно. Поэтому найдем вначале модули ее составляющих _X и _Y, а затем с помощью теоремы Пифагора вычислим модуль самой силы :

F = 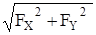. (18.1)

Какие законы следует применять? Законы Ньютона применимы к частицам. Сплошной стержень можно считать состоящим из частиц, но этих частиц бесконечно много, так что безнадежно пытаться к каждой из них применять «персональную тройку» законов Ньютона. К счастью, имеется обходной путь. Поскольку деформации стержня не существенны, его можно считать абсолютно твердым телом. Он находится в равновесии. Так что нужно применить условия равновесия абсолютно твердого тела.

Вспомним, в чем заключаются условия равновесия абсолютно твердого тела, и научимся ими пользоваться. Одно из них (условие равновесия для сил) состоит в равенстве нулю суммы всех сил, приложенных к телу. Это условие обеспечивает равенство нулю ускорения центра масс. Его часто записывают в проекциях на удобным образом выбранные оси. Как направить эту ось в данном случае? Желательно, чтобы при этом оказалось как можно меньше неизвестных проекций сил. В данном случае такому условию удовлетворяет ось y (рис. 34):

F_Y – m g = 0. (18.2)

В это уравнение входит единственное неизвестное F_Y, благодаря тому, что сила _X и сила натяжения нити 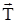(рис. 34) дают нулевые проекции на вертикальное направление.

Каким условием нужно воспользоваться для нахождения F_X? Если записать условие равновесия сил в проекциях на горизонтальную ось x, то в уравнении помимо искомой величины F_X войдет еще и неизвестная сила натяжения нити T. Поэтому обратимся ко второму условию равновесия абсолютно твердого тела – условию равновесия для моментов сил. Оно заключается в равенстве нулю суммы моментов всех сил, приложенных к телу, относительно произвольно выбранной оси. Это условие обеспечивает отсутствие поворотов тела под действием приложенных сил. Как целесообразно выбирать указанную ось? Выбор должен быть сделан так, чтобы в получаемых уравнениях было поменьше неизвестных величин.

Относительно какой же оси следует записывать условие равновесия для моментов сил в данной задаче? Если линия действия силы пересекает ось, относительно которой ищется момент, то этот момент равен нулю, поскольку равно нулю плечо силы. По этой причине для нахождения F_Y ось должна проходить через точку O, чтобы плечо неизвестной силы 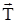оказалось равным нулю. Для нахождения T нужно взять ось, проходящую через точку A. Из этих соображений получаем

– m g (l / 2) cos a + F_Y l cos a – F_X l sin a = 0, (18.3)

m g (l / 2) cos a – T l sin a = 0. (18.4)

Моменты сил, поворачивающих стержень по часовой стрелке, берутся положительными, а поворачивающие в противоположном направлении – отрицательными. Плечо силы _X относительно оси O равно l sin a, а плечо силы _Y – l cos a (рис 34). Сила тяжести m приложена в центре стержня, поскольку он однородный. Плечо этой силы равно (l / 2) cos a, как относительно оси O, так и относительно оси A. Плечо силы T относительно оси A равно l sin a.

Величину T находим непосредственно из (18.4):

T = (1 / 2) m g ctg a = 4,9 Н.

Подставив (18.2) в (18.3), найдем F_X и получим из (18.1)

F = m g 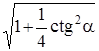» 11 Н.

Если a ® p / 2, то сила F ® m g. Это вполне естественно, так как при вертикальном положении стержня сила тяжести будет уравновешиваться только силой реакции шарнира A.

В копилку опыта

· Решая задачи статики, к твердым телам конечных размеров применяют условия равновесия абсолютно твердого тела.

· При записи условия равновесия для сил ось проецирования целесообразно направлять перпендикулярно «лишним» неизвестным силам.

· Условия равновесия для моментов сил лучше записывать относительно осей, подобранных так, чтобы плечи «лишних» неизвестных сил были равны нулю.

 

Если хочешь научиться