Законы Ньютона позволяют единообразно описывать и движение грузов, брусков, шариков в пределах лабораторной установки, и движение различных транспортных средств, и движение спортсменов, и движение космических тел, как естественных, так и искусственных. Единообразие обусловлено тем, что все эти объекты моделируются частицами – материальными точками.
Задача 15. 1. На подставке лежит груз, к которому прикреплена пружина, подвешенная к потолку. В начальный момент пружина не растянута. Подставку начинают опускать вниз с ускорением a. Через какое время груз оторвется от подставки? Жесткость пружины – k, масса тела – m.
На рисунке 24 слева показано положение груза в начальный момент времени, а справа – в момент времени t. 
– перемещение конца пружины за это время.
Какие законы следует применить для нахождения t? Груз можно считать частицей. Пока он не оторвется от подставки, его ускорение равно 
. Так что можно применить соотношения (3.6) – (3.8) кинематики частицы, движущейся с постоянным ускорением. Какие именно уравнения здесь целесообразно использовать? Применим уравнение (3.6) для перемещения в проекции на ось x (рис. 24):
S = a t2 / 2. (15.1)
Достаточно ли этого уравнения? Нет, не известно S. Какие еще законы следует привлеть? Величина S связана с силой упругости пружины, а сила упругости – с другими силами и ускорением, ими обусловленным. Так что нужно воспользоваться формулой (13.3) и законами Ньютона.
Запишем закон Гука (13.3) для силы упругости F (рис. 24):
F = k S. (15.2)
Теперь «запрягаем тройку» законов Ньютона.
В качестве инерциальной можно взять систему отсчета «Потолок», или «Лабораторию». Ускорение предполагается заданным именно в этой системе отсчета. С таким ускорением движутся подставка и груз, пока он на нее опирается. Применим второй закон Ньютона для груза. Силы, приложенные к нему, указаны на рисунке 24: m 
– сила тяжести, 
– сила реакции подставки. В момент отрыва груза от опоры последняя сила становится равной нулю. В проекции на ось x (рис. 24) второй закон Ньютона дает для этого момента времени
m a = m g – F. (15.3)
Получено три уравнения, содержащие три неизвестные: t, S, F. Поскольку в задаче нужно найти t, исключаем вначале остальные неизвестные. Из (15.3) и (15.2) получаем
m a = m g – k S. (15.4)
Затем выражаем S из (15.4) и подставляем в (15.1):
m (g – a) / k = a t2 / 2 Þ t = 
.
|
В копилку опыта
· Третий закон Ньютона в данном случае «остается в резерве», зато пришлось привлечь кинематику и закон Гука. Подобные ситуации встречаются и в других задачах.
Задача 15. 2. На полу кабины лифта, движущегося вверх с постоянным ускорением a, находится брусок массой m. К бруску под углом a к горизонту приложена сила. Определить эту силу, если брусок относительно лифта движется равномерно и прямолинейно. Коэффициент трения между бруском и полом лифта равен m.
Из А нализа условия ясно, что придется «запрягать тройку» законов Ньютона, поскольку фигурируют динамические величины m и F. К какой частице их следует применить? Применить их нужно к бруску, который можно считать частицей, потому что он движется поступательно.
Применяя первый закон Ньютона, следует указать инерциальную систему отсчета. Только в ней можно записывать уравнения второго закона Ньютона. Наиболее просто выглядит движение бруска относительно кабины лифта: он движется равномерно, то есть с нулевым ускорением. Можно ли в системе «Лифт» записывать второй закон Ньютона? Нет. Так можно было бы поступать только в том случае, если бы лифт двигался равномерно относительно инерциальной системы отсчета «Земля». В данном случае это не так, поэтому следует записывать динамические уравнения непосредственно в системе отсчета «Земля». Каково же ускорение бруска в этой системе отсчета? Как его можно найти, используя данные условия? Следует применить закон сложения ускорений (3.5):
БЗ = БЛ + ЛЗ = 0 + ЛЗ = .
Здесь БЗ – ускорение бруска относительно Земли, БЛ = 0 – ускорение бруска относительно лифта, а ЛЗ = – ускорение лифта относительно Земли.
Теперь нужно применить второй закон Ньютона. Для этого следует указать силы, приложенные к бруску (рис. 25): m – сила тяжести, – сила нормальной реакции, 
ТР – сила трения скольжения, – заданная в условии задачи сила. Сила может быть направлена или так, как показано сплошной стрелкой на рисунке 25, или так, как показано пунктирной стрелкой.
Неужели придется по отдельности рассматривать каждый из этих случаев? Нельзя ли «одним ударом сразу убить двух зайцев»? В данном случае можно, если считать угол a, под которым эта сила наклонена к горизонту, положительным в случае сплошной стрелки и отрицательным в случае пунктирной.
Записываем уравнение второго закона Ньютона для движения бруска относительно инерциальной системы отсчета «Земля» в проекции на ось y (рисуок 25):
m a = N – m g + F sin a. (15.5)
В случае сплошной стрелки последнее слагаемое положительно, в случае пунктирной – отрицательно. Так что уравнение (15.5) учитывает оба возможных направления силы .
Достаточно ли полученного уравнения для решения задачи? Нет, поскольку в уравнении две неизвестные величины: F и N. Какое еще уравнение, содержащее N, можно привлечь? Все ли данные задачи учтены? Не использована пока величина m, поэтому следует записать еще уравнение (13.7):
FТР = m N. (15.6)
Но в этом уравнении содержится неизвестное – FТР. Приходится искать еще одно уравнение, в которое входит FТР. Какой закон для этого нужно использовать? Силы содержатся во втором законе Ньютона, который уже учтен в уравнении (15.5). Но учет этот проведен «однобоко»: векторное равенство записано в проекции лишь на ось y. Запишем тот же закон, но в проекции на ось x (рис. 25):
0 = F cos a – FТР. (15.7)
Получено три независимых уравнения, содержащие три неизвестных. Этого достаточно для нахождения решения. Исключая N и FТР из системы уравнений, получим ответ (проделайте преобразования самостоятельно):
F = 
. (15.8)
А нализ результата приводит к знакомым из жизненного опыта заключениям. Чем больше величины m и m, тем большую силу нужно приложить для перетаскивания груза. При a > 0 (сплошная стрелка на рис. 25) сила F должна быть меньше, чем при a < 0 (пунктирная стрелка) – тянуть легче, чем толкать.
В копилку опыта
· 
Переход в инерциальную систему отсчета осуществляется посредством закона сложения ускорений (3.5).
· Записывая уравнения второго закона Ньютона в проекции на различные оси, получаем независимые уравнения.
· Использование положительных и отрицательных значений некоторых величин (a) иногда позволяет «убить двух зайцев сразу».
Задача 15. 3. Шар массой m и объемом V падает с постоянной скоростью v в жидкости, плотность которой равна r. С какой силой нужно тянуть этот шар вверх, чтобы он поднимался в той же жидкости со скоростью 2v?
Можно ли к рассматриваемому в задаче шару применить законы Ньютона? Каково ускорение шара? В какой системе отсчета подразумевается движение? Является ли она инерциальной? Какие силы приложены к шару?
Ответив на эти вопросы, посмотрите на рисунок 26. Слева показаны силы, приложенные к шару, движущемуся вниз, справа – вверх. m – сила тяжести шара. А – выталкивающая сила жидкости (сила Архимеда). Она вычисляется по формуле
FА = r g V. (15.9)
C – сила сопротивления, определяемая соотношением (13.6).
Примените второй закон Ньютона в проекциях на ось x (рис. 26) для обоих случаев. Сравните полученные уравнения с записанными ниже выражениями:
0 = m g – k v – r g V, (15.10)
0 = m g + 2 k v – F – r g V. (15.11)
Из этой системы уравнений найдите F и сравните с ответом:
F = 3 g (m – r V). (15.12)
Результат не зависит от скорости v и имеет смысл только при условии, что m / V > r, то есть при достаточно большой плотности шара.
В копилку опыта
· Сила сопротивления в жидкости (или в газе) может обеспечить равномерное движение тел благодаря ее зависимости от скорости.
· Применяя законы Ньютона, следует знать свойства и особенности сил, о которых идет речь (силы Архимеда, сил сопротивления, …).
Задача 15. 4. На экваторе некоторой планеты ускорение свободного падения втрое меньше, чем на полюсе. Период обращения этой планеты вокруг своей оси равен 55 мин. Определите среднюю плотность планеты.
А нализ условия требует выяснения причин того, что ускорение свободного падения на экваторе (g) меньше, чем на полюсе (g0). Чем это может быть обусловлено? Очевидно, это связано с вращением планеты. Чем свободное падение тел на экваторе отличается от свободного падения на полюсе? Когда говорят об ускорении свободного падения, то какая система отсчета подразумевается? Подразумевается лаборатория, в которой исследуется падение – система отсчета «Лаборатория» (Л на рис.27а). Она неподвижна относительно поверхности планеты в данном месте и вращается вместе с планетой. На экваторе лаборатория вращается по окружности, радиус которой равен радиусу планеты R (рис. 27а), и, следовательно, движется с центростремительным ускорением (13.10):
aЦ = w2 R = (2 p / T)2 R. (15.13)
На полюсе радиус траектории, по которой движется лаборатория, и, следовательно, ее ускорение равны нулю. В какой системе отсчета происходит указанное вращение? Эта система отсчета связана с осью вращения планеты и с далекими звездами – система отсчета «Звезды» (рис. 27а). Какая из указанных систем является инерциальной? Инерциальной является система «Звезды», относительно которой «Лаборатория» движется с ускорением.
Итак, различие величин g и g0 обусловлено тем, что в одном случае ускорение системы отсчета определяется формулой (15.3), а в другом оно равно нулю. Это различие отражено на рисунках 27б и 27в. Здесь же показана гравитационная сила , действующая со стороны планеты.
В системе отсчета «Звезды» можно записать уравнение второго закона Ньютона. В проекции на ось x получим:
на полюсе – m g0 = F, (15.14)
на экваторе – m aТЗ = F. (15.15)
Гравитационная сила F определяется формулой (13.4):
F = G m M / R2, (15.16)
где M – масса планеты.
Ускорение ТЗ тела относительно системы отсчета «Звезды» находится из закона сложения ускорений (3.5):
ТЗ = ТЛ + ЛЗ = + Ц Þ
aТЗ = g + aЦ. (15.17)
Какие еще соотношения нужно привлечь для решения задачи? Массу планеты M нужно выразить через искомую плотность r:
M = r 4 p R3 / 3, (15.18)
а также учесть, что g0 / g = 3.
Найдите из полученной системы уравнений r и сравните с ответом
r = 9 p / (2 G T2).
В копилку опыта
· Ускорение свободного падения зависит от широты местности: оно уменьшается при переходе от полюса к экватору. Аналогично меняется и сила тяжести. Обусловлено это вращением планеты.
· Чтобы учесть эффекты, связанные с вращением планет, в качестве инерциальной нужно брать систему отсчета «Звезды».
Не поскользнуться бы
С силой трения между твердыми телами мы сталкиваемся буквально на каждом шагу. Без ее участия не обходится движение любого механизма. Естественно, с этой силой приходится встречаться при решении многих задач.
Задача 16. 1*. При каком минимальном коэффициенте трения между обувью и беговой дорожкой спринтер может пробежать стометровку за 10 с, если он увеличивает свою скорость лишь на первых 20 м дистанции?
На рисунке 28 показаны: перемещение 1 на участке разгона, где спортсмен в течение времени t1 движется с ускорением ; все перемещение за время t; сила тяжести m ; сила нормальной реакции ; сила тяги , развиваемая спортсменом при разгоне.
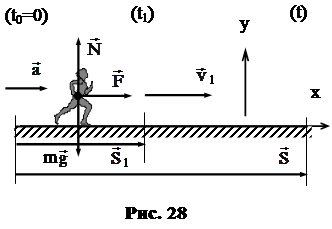Каков механизм возникновения силы тяги? Спортсмен отталкивается от беговой дорожки. Иначе говоря, он действует на дорожное покрытие силой трения, направленной назад, вследствие чего по третьему закону Ньютона на спортсмена со стороны дороги действует сила трения покоя, направленная вперед. Последняя и представляет собой силу тяги.
Можно ли в данной задаче применить известные вам законы динамики? Можно, поскольку модель частицы для спортсмена в данном случае приемлема. Для какого этапа движения следует применить законы Ньютона? Сила трения, коэффициент которой нужно найти, имеет наибольшее значение на участке разгона, для него и следует записывать уравнения динамики.
Какую систему отсчета нужно выбрать? Естественно использовать систему «Стадион». Именно относительно нее задаются характеристики движения спортсменов. Эта система отсчета инерциальная, так что в ней можно записывать уравнение второго закона Ньютона.
В выбранной инерциальной системе отсчета запишем уравнение второго закона Ньютона в проекции на ось x (рис. 28):
F = m a. (16.1)
Интересующая нас сила тяги F равна максимальной силе трения покоя, определяемой формулой (13.8),
F = m N. (16.2)
Сила нормальной реакции N находится из уравнения второго закона Ньютона, записанного для оси y (рис. 28),
N = m g. (16.3)
Для нахождения ускорения a используем кинематическое уравнение (4.7) (рис. 28):
v1 = a t1. (16.4)
Следует применить также кинематическое уравнение (4.6) для перемещений 1 и (рис. 28):
S1 = a t12 / 2, (16.5)
S – S1 = v1 (t – t1). (16.6)
Найдите из полученной системы уравнений величину m и сравните с ответом:
m = 
» 0,36. (16.7)
Из (16.7) следует, что величина m должна быть тем больше, чем за меньшее время t спортсмен намерен пробежать дистанцию, иначе он может поскользнуться на старте.
В копилку опыта
· Сила тяги, развиваемая человеком, также как и двигателем автомобиля, определяется силой трения (силой сцепления с дорожным покрытием).
· При решении многих задач механики законы Ньютона применяются совместно с уравнениями кинематики.
Задача 16. 2. С какой скоростью может ехать мотоциклист по закруглению горизонтальной дороги, если радиус закругления – r, а коэффициент трения колес о дорогу – m? На какой угол от вертикального положения он при этом должен наклониться?
На рисунке 29 схематически изображен мотоциклист, скорость которого направлена за плоскость рисунка. Он поворачивает направо, вследствие чего движется с центростремительным ускорением . На мотоциклиста действует дорога с силой 
, которую целесообразно представить в виде двух составляющих:
= + ТП. (16.8)
Составляющая Направлена вертикально. Она обусловлена деформацией полотна дороги. Составляющая ТП – сила трения покоя. Она направлена в сторону, противоположную возможному перемещению колеса относительно дороги. Если бы трение исчезло, то колесо соскользнуло бы налево, поскольку мотоциклист по инерции удалялся бы от центра кривизны траектории.
Сила тяжести m приложена в центре масс (центре тяжести) мотоциклиста с мотоциклом.
Можно ли считать мотоциклиста частицей? Вообще говоря, нет, поскольку о наклоне на угол a можно говорить только для тела конечных размеров. Как же в этом случае поступать? Вспомним, чем замечательна точка, называемая центром масс. Если бы в ней была сосредоточена масса всей системы, то получившаяся в результате этого частица двигалась бы так же, как эта точка. Так что законы Ньютона можно приинять к частице, обладающей массой всей системы и находящейся в центре масс. Но мало знать, как движется центр масс, нужна информация о движении всех остальных точек. Если речь идет об абсолютно твердом теле (таковым будем считать мотоциклиста с мотоциклом), то оно может вращаться в поступательно движущейся системе отсчета, связанной с центром масс (Ц-системе). Вращение мотоциклиста в Ц-системе означает его падение. Чтобы этого не произошло, сумма моментов всех сил, приложенных к мотоциклисту, относительно центра масс должна быть равна нулю. Тогда все точки будут двигаться так же, как и центр масс. Только в этом случае мотоциклиста можно считать частицей и применять к нему законы Ньютона.
Применим второй закон Ньютона для мотоциклиста, считая его частицей, движущейся с центростремительным ускорением a = v2 / r. В проекции на ось x (рис. 29) получим
m v2 / r = FТП, (16.9)
а в проекции на ось y –
0 = N – m g. (16.10)
Поступательное движение мотоциклиста будет обеспечено, если лежит на прямой, проходящей через центр масс (центр тяжести). В этом случае момент силы , или сумма моментов и ТП равны нулю, поскольку равно нулю плечо силы , точно так же, как и силы m . При указанной ориентации вектора угол a, как видно из рисунка 29, определяется соотношением
tg a = FТП / N. (16.11)
Cила трения покоя удовлетворяет условию (13.8). Учтем также соотношение (16.10)
FТП £ m N = m m g. (16.12)
Подставляя (16.9) в (16.12), получим:
m v2 / r £ m m g Þ v £ vП = 
. (16.13)
Чтобы не поскользнуться на повороте, мотоциклист должен ехать со скоростью, не превышающей некоторого предельного значения vП, которое тем меньше, чем меньше коэффициент трения m и чем круче поворот (меньше r).
Из (16.11), (16.9) и (16.10) найдем, на какой угол он должен наклониться:
tg a = 
Þ a = arctg (v2 / r g). (16.14)
С учетом неравенства (16.13) получим из (16.14):
tg a £ m. (16.15)
Равенство (16.14) показывает, что с увеличением скорости v должен увеличиваться угол наклона a, иначе можно «не вписаться в поворот» (увеличится r). Однако тангенс угла наклона должен оставаться меньше коэффициента трения m (см. (16.15)).
|
· Применяя законы Ньютона к телу конечных размеров, можно найти, как движется центр масс этого тела.
· Моменты внешних сил относительно центра масс определяют, будет ли тело (абсолютно твердое) двигаться поступательно, или же эти силы вызовут его поворот относительно поступательно движущейся системы отсчета, связанной с центром масс (Ц-системы).
· При решении физических задач иногда приходится иметь дело не только с уравнения ми, но и с неравенствами. Неравенства могут содержаться и в ответах.
Задача 16. 3*. При торможении всеми четырьмя колесами тормозной путь автомобиля равен S. Найти тормозной путь этого же автомобиля при торможении только передними колесами (S1) и только задними – (S2). Коэффициент трения скольжения колес равен 0,80. Центр тяжести автомобиля расположен на одинаковом расстоянии от передних и задних колес на высоте, составляющей 1 / 4 часть расстояния между осями автомобиля.
На рисунке 30 изображены: сила тяжести m автомобиля; силы нормальной реакции 1 и 2 со стороны дороги; силы трения скольжения 1 и 2, действующие при торможении на колеса; перемещение автомобиля ; скорость 
и ускорение при торможении; расстояние между осями l; высота h центра масс над полотном дороги.
Какие физические законы здесь следует применить? Встречалась ли вам задача чем-то похожая на данную? Как и в предыдущей задаче, здесь речь идет о движении тела конечных размеров, так что придется анализировать движение центра масс и возможные повороты автомобиля в Ц-системе, считая его абсолютно твердым телом. Из каких уравнений непосредственно определяются искомые величины S1 и S2? Они определяются из кинематических уравнений движения центра масс. Поскольку центр масс автомобиля движется при торможении с постоянным ускорением , можно применять кинематические уравнения (4.6) – (4.8).
Применяя кинематическое уравнение (4.8) для перемещения в проекции на ось x (рис. 30), получим
S = v2 / (2 a). (16.16)
Для искомых величин S1 и S2 можно написать аналогичные соотношения:
S1 = v2 / (2 a1) и S2 = v2 / (2 a2). (16.17)
Какие неизвестные помимо S1 и S2 входят в полученные уравнения, и из каких законов их можно найти? Неизвестные ускорения a, a1 и a2 можно найти из законов Ньютона в проекции на ось x (рис.30).
Для случая торможения всеми колесами получим
– m a = – F1 – F2. (16.18)
Кроме того, на основании (13.7) имеем
F1 = m N1 и F2 = m N2,
а из второго закона Ньютона в проекции на вертикальную ось следует, что
N1 + N2 = m g.
Поэтому из (16.18) получается a = m m g, и после подстановки в (16.16) –
S = v2 / (2 m g). (16.19)
При торможении только передними колесами F2 = 0, поэтому вместо соотношения (16.18) будем иметь
m a1 = F1 = m N1. (16.20)
Для нахождения N1 помимо соотношения N1 + N2 = m g следует учесть также равенство нулю суммы моментов относительно центра масс всех сил, приложенных к автомобилю:
l (N1 – N2) / 2 – m N1 h = 0. (16.21)
Выполнение этого условия обеспечивает поступательное движение автомобиля в инерциальной системе отсчета. Из последней пары уравнений получаем
N1 = 
(16.22)
и после подстановки в (16.20) –
a1 = 
. (16.23)
В случае торможения только задними колесами выполняются соотношения, аналогичные (16.20) и (16.21):
m a2 = F2 = m N2 ,
l (N1 – N2) / 2 – m N2 h = 0.
Эти соотношения дают вместо (16.23):
a2 = 
. (16.24)
Подстановка (16.23) и (16.24), а также (16.19) в (16.17) приводит к таким ответам:
S1 = 2 S (1 – m h / l) = 1,6 S; S2 = 2 S (1 + m h / l) = 2,4 S.
В обоих случаях тормозной путь больше, чем при торможении всеми колесами, но тормоза на передних колесах более эффективны, чем на задних.
В копилку опыта
· 
Силы трения, действующие на колеса автомобиля, создают вращающий момент относительно центра масс. Этот момент приводит к перераспределению сил реакции дороги и может привести к опрокидыванию автомобиля.
· При поступательном движении тела в инерциальной системе отсчета сумма моментов всех сил, приложенных к телу, равна нулю, если эти моменты вычисляются относительно цетра масс.
