«Кинематика – раздел механики, изучающий изменение с течением времени положения одних тел относительно других. Кинематика отвечает на вопрос «как движется тело?», без выяснения причин конкретного вида движения.
«Материальная точка (или частица) – модель реального тела, мысленно лишенного размеров. Эта модель может быть использована, если выполняется одно из следующих условий: а) размеры тела пренебрежимо малы по сравнению с существенными в данной задаче расстояниями; б) если тело совершает поступательное движение, то есть все его точки движутся одинаковыми образом.
«Переход от реальных тел к моделям – важнейший этап физического исследования. Без него невозможно использовать математику.
«Задать систему отсчета – значит указать тело отсчета. Под телом отсчета понимают предмет, относительно которого анализируется движение других тел. Принято говорить: «система отсчета – «Земля»; система отсчета – «ракета»; система отсчета – «поезд»; и т.д.».
«Для численного описания движения вводят систему координат. Часто ее включают в понятие «система отсчета». Здесь это не делается, чтобы облегчить применение понятия «система отсчета» и стимулировать рациональный выбор системы координат. При таком подходе упрощается введение системы отсчета, после чего сохраняется возможность свободного варьирования системы координат.
«Перемещение частицы 
(или 
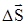) – направленный отрезок, соединяющий начальное ее положение с конечным.
«Скоростью частицы 
называют величину, равную отношению перемещения 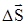за малый промежуток времени Dt, примыкающий к рассматриваемому моменту, к этому промежутку:
= 
. (4.1)
Промежуток считается малым, если его уменьшение практически не влияет на результат (4.1). В более строгом определении, доступном ученикам 11 класса, предполагается, что Dt ® 0, то есть скорость является производной по времени от перемещения. Скорость характеризует движение в определенный момент времени, в определенной точке траектории. Она направлена по касательной к траектории.
«Ускорением 
называют величину, равную отношению изменения скорости 
за малый промежуток времени Dt, примыкающий к рассматриваемому моменту, к этому промежутку:
= 
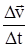. (4.2)
Смысл малости Dt в (4.2) аналогичен тому, который обсуждался в связи с формулой (4.1). Ускорение – мгновенная характеристика движения. Направлена эта векторная величина в сторону вогнутости траектории. Только в конкретных случаях можно говорить о более точном направлении.
«В общем случае ускорение обычно разлагают на две составляющие t и n:
= t + n. (4.3)
Вектор t – тангенциальное ускорение. Оно направлено по касательной к траектории и характеризует изменение модуля скорости, n – нормальное ускорение. Оно направлено перпендикулярно к касательной и характеризует изменение направления скорости.
«Закон сложения скоростей связывает скорости трех тел, движущихся поступательно друг относительно друга:
12 = 13 + 32. (4.4)
Здесь, например, 32 обозначает скорость третьего тела относительно второго. Термины «подвижная» и «неподвижная» системы отсчета лучше не использовать, так как они могут приводить к забвению относительности движения и затруднять решение задач.
«Закон сложения ускорений аналогичен (4.4):
12 = 13 + 32. (4.5)
Если = const, то для произвольной оси x справедливы соотношения
SX = v0X t +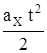 
, (4.6)
vX = v0X + aX t, (4.7)
SX = 
. (4.8)
В этих формулах индекс X указывает на проекцию соответствующей величины на ось x, а индекс 0 относится к начальному моменту времени.
«Если частица движется по окружности радиуса R, то модуль скорости равен
v = w R, (4.9)
а модуль нормального ускорения –
an = v2 / R = w2 R. (4.10)
Здесь w – угловая скорость, то есть отношение угла поворота Dj радиуса окружности, проходящего через движущуюся частицу, к малому промежутку времени Dt, за который происходит этот поворот:
w =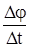 
. (4.11)
Смысл малости промежутка Dt, аналогичен малости Dt в формулах (4.1) и (4.2).
Приведенных выше положений и формул достаточно для решения почти всех школьных задач кинематики. Именно в таком виде их легче запомнить и проще применять.
Формулы (4.4) и (4.5) вы всегда сможете записать, если обратите внимание на расположение индексов. Индекс 3 помещается между индексами 1 и 2. Записав формулу, не трудно прочитать словами закон сложения скоростей: скорость тела 1 относительно тела 2 равна сумме скоростей тела 1 относительно 3 и тела 3 относительно 2. При решении задач вместо цифр удобно использовать первые буквы названий конкретных тел. В данном случае, формализм способствует лучшему осознанию физического смысла закона – редкое исключение из правила!
Формула (4.7) может быть выведена из (4.6) и (4.1), а формула (4.8) – из (4.6) и (4.7). Однако все эти формулы отнесены к «генерал-законам», поскольку каждую из них часто приходится применять.
Формулы (4.6) – (4.7) иногда записывают в векторной форме. При необходимости к этой форме можно перейти, заменив значки проекций (индексы X) на значки векторов (стрелки над буквами). Но чаще всего приходится работать именно с проекциями. Кроме того, описанная процедура перехода к векторной форме не применима к (4.8), так как нельзя делить на вектор ().
«Иногда формулу (4.6) записывают иначе, осуществляя замену
SX = x – x0, (4.12)
где x0 – координата частицы в начале перемещения. Таким образом получается уравнение для координат частицы. Если в задаче речь идет именно о координатах, то замену (4.12) следует произвести. Но чаще всего так поступать не нужно, поскольку интерес обычно представляет именно перемещение.
В приведенных выше формулах фигурируют векторные величины и их проекции. Векторные величины встречаются и в других разделах физики. Нужно уметь оперировать этими величинами, в частности, складывать их и находить проекции на оси координат.
«Векторная физическая величина (вектор) характеризуется не только числом (модулем), но и направлением в пространстве. В отличие от этого скаляр характеризуется только числом (объем, масса, электрический заряд и др.). Векторная физическая величина обычно изображается направленным отрезком (геометрическим вектором). При этом длина направленного отрезка в определенном масштабе отражает модуль физической величины. Масштаб обычно на рисунках не указывается. Но не следует забывать о его существовании при сравнении направленных отрезков, изображающих векторные величины. Проверьте себя, ответив на приведенные ниже вопросы.
На рисунке 1 изображены кинематические векторные величины. Что больше: а) или 1; б) 2 или 3? Равны ли величины: в) v1 и v2; г) и 3.
Уловили ли вы бессмысленность вопросов а) и г)? Не ошиблись ли, отвечая на вопросы б) и в)? Векторные величины, не совпадающие по направлению, можно сравнивать только по модулю.
«
Векторные величины складываются по правилу треугольника. Рисунок 2 иллюстрирует это правило.
«Вычитание векторов сводится к сложению:
= 1 – 2 = 1 + (– 2).
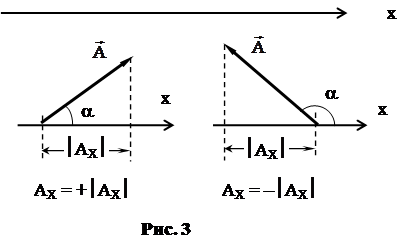
«Проекцией вектора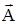 
на ось x называют величину
AX = A cos a, (4.13)
где a – угол, образованный вектором 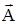с направлением оси x. Если векторную величину изобразить геометрическим вектором, то модуль проекции будет представлен на рисунке катетом прямоугольного треугольника с гипотенузой 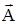, который изображен на рисунке 3. Знак проекции совпадает со знаком cos a. Проекция положительна, если угол a острый, и отрицательна, если он тупой. При нахождении проекции не следует забывать, что искомый катет выражает модуль проекции в тех же единицах и в том же масштабе, в которых соответствующая гипотенуза выражает векторную величину.
 |
В качестве алгоритма нахождения проекции вряд ли целесообразно запоминать длинный текст, в котором говорится о том, что «… нужно идти от проекции начала к проекции конца вектора…». Достаточно вспомнить формулу (4.13) или отражающий ее рисунок 3.
