Задача 6. 1 На горе с уклоном 300 бросают мяч со скоростью 10 м/с перпендикулярно склону горы. Найти время полета мяча. На каком наибольшем расстоянии от поверхности горы окажется мяч во время полета? Где он приземлится?
На первый взгляд кажется, что задача много сложнее предыдущей, ведь здесь идет речь о движении по криволинейной траектории. Не пугайтесь. Дерзайте и победите!
Какое уравнение нужно применить для нахождения t? Чем замечателен этот момент времени? Мяч снова оказывается на склоне горы. В какой же из формул (4.6) – (4.8) это обстоятельство может найти отражение? Известно ли что-либо о скорости или перемещении для этого момента времени? О скорости ничего не известно, а о перемещении 
известно, что оно направлено вдоль склона горы (рис. 5). Определяет ли это какую-либо проекцию перемещения? Да, проекция на направление, перпендикулярное склону горы, равна нулю. Так каким же уравнением следует воспользоваться? Следует применить уравнение (4.6) для перемещения в проекции на ось y (рис. 5):
0 = v t – 
. (6.1)
Здесь учтено, что v0Y = v;
aY = – g cos a, так как угол, образованный вектором 
и осью y, равен p – a. Углы, обозначенные на рисунке 5 буквой a, одинаковы, поскольку имеют взаимно перпендикулярные стороны (помечены черточками).
Нулевой корень уравнения (6.1) не соответствует условию задачи, а второй корень дает ответ
t = 
. (6.2)
Какое уравнение следует применить для нахождения l? Ясно, что придется иметь дело с перемещением 1 (рис. 5) до точки траектории, которая находится дальше всего от поверхности горы. Чем еще замечательна эта точка? Известно ли что-либо об относящихся к ней характеристиках движения? Известно, что скорость направлена по касательной. А куда направлена касательная в этой точке? Она, кажется, направлена вдоль склона. Проверим эту гипотезу.
Когда угол наклона скорости 
1 к поверхности горы положителен, мяч удаляется от склона; когда этот угол отрицателен, мяч приближается. Следовательно, в самой дальней точке он должен быть равным нулю. Высказанная выше гипотеза соответствует действительности. А это означает, что проекция 1 на ось y равна нулю.
Так какую же формулу следует использовать? Следует применить формулу (4.8) в проекции на ось y, перпендикулярную склону горы. Находим:
vY = 0; v0Y = v; aY = – g cos a; SY = l; Þ
l = 
= 
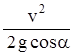. (6.3)
Какую формулу следует применить для нахождения S? Очевидно, формулу для перемещения в проекции на ось x (рис. 5). Формула (4.8) предполагает использование неизвестной скорости в момент падения, а в (4.6) входит найденное выше значение времени t (6.2). Применяя (4.6) и подставляя (6.2), получаем: SX = S; v0X = 0; aX = g sin a;
S =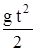 
sin a = 
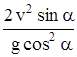. (6.4)
При анализе результатов полезно перейти к пределу при a ® 0. Ответы этой более простой задачи о движении тела, брошенного вертикально вверх, совпадают с полученными предельными выражениями.
Проверьте наименования, оцените ответы, вычислите, округлите и сравните с приведенными здесь значениями: t = 2,3 с; l = 5,9 м; S = 14 м.
В копилку опыта
· «Генерал-законы» (4.6) – (4.8) применяются и для криволинейного движения.
· Для записи одного уравнения можно использовать одну ось, а для записи другого – другую.
Разделяй и властвуй
Задача 7. 1*. Ракета стартует с земли вертикально вверх с постоянным ускорением a и через время t падает на землю. Сколько времени работал двигатель?
| Ракета a t t1 –? | Размерами ракеты и сопротивлением воздуха пренебрегаем. Высоту полета ракеты будем считать много меньше радиуса земного шара, так что ускорение свободного падения в любой точке траектории одно и то же и равно 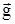 . В результате сделанных приближений приходим к кинематике частицы.
| |
Можно ли все рассматриваемое движение описать законами (4.6) – (4.8)? Нет, так как ускорение ракеты не остается неизменным.
Можно ли данную задачу разбить на более простые, для которых применимы эти уравнения? Когда работал двигатель, ракета двигалась вверх с ускорением  . Потом она продолжала движение вверх с уменьшающейся по модулю скоростью. После достижения верхней точки траектории началось ее свободное падение вниз. Сколько же подзадач целесообразно выделить? Можно выделить три подзадачи. Чем отличаются два последних этапа движения и что у них общего?
| ||
Сначала ракета двигалась вверх, а затем – вниз, но ускорение в обоих случаях одно и то же – 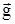. Зачем же различать эти этапы движения? Ведь формулы (4.6) – (4.8) описывают все движение с постоянным ускорением, не зависимо от направления скорости. Поэтому эти формулы целесообразно применять отдельно для первого (активного), этапа, когда работал двигатель, и для всего второго (пассивного), включающего движение и вверх, и вниз.
Какие формулы следует использовать для первого этапа? Время входит и в (4.6), и в (4.8). В одной из них фигурирует неизвестное перемещение, а в другой – неизвестная скорость. Определить время из одного уравнения не удается. Приходится записывать оба уравнения.
Применяем формулу (4.6) к перемещению 
1 в проекции на ось x (рис. 6):
S1 = a t12 / 2. (7.1)
Здесь SX = S; v0X = 0; aX = a.
Применяем формулу (4.7) для момента времени t. Используем ту же ось x (рис. 6):
v1 = a t1. (7.2)
Полученные два уравнения содержат три неизвестные величины: t, S и v1. Необходимо еще одно уравнение, связывающее некоторые из них. Какую формулу следует для этого применить? Какие данные условия еще не использованы? Не использована заданная величина t, а также не отражено движение на втором этапе (пассивном). Как связать величины t1 и t? Время движения на втором этапе равно t – t1. Какие характеристики движения на этом этапе могут быть связаны с неизвестными, входящими в уравнения (7.1) и (7.2)? Перемещение (рис. 6) равно – 1, а начальная для этого этапа скорость равна 1. Так какую же формулу следует применить? Нужно применить формулу (4.6) для перемещения . Можно использовать ту же ось x (рис. 6). Получим
– S1 = v1 (t – t1) – g (t – t1)2 / 2. (7.3)
Решаем систему уравнений (7.1) – (7.4). Подставляем (7.1) и (7.2) в (7.3) и преобразуем:
(a + g) t12 – 2 t (a + g) t1 + g t2 = 0. (7.4)
Квадратное уравнение (7.4) имеет два корня:
t1 = t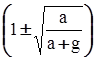 
. (7.5)
Какой физический смысл имеют эти корни? Если в (7.5) взять знак «+», то получится t1 > t, что не удовлетворяет условию задачи: время активного этапа меньше времени всего движения. Поэтому в ответе следует оставить только знак «–»:
t1 = t 
. (7.6)
В копилку опыта
· 
В задачах с абстрактным содержанием (нет конкретных чисел) нужно иметь в виду любые возможные значения используемых величин. Допустимы и некоторые разумные ограничения. В данной задаче время t предполагается не очень большим, чтобы можно было пренебречь зависимостью g от высоты полета.
· Задача разбивается на две подзадачи: о движении с ускорением 
и о движении с ускорением .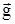
· При движении с ускорением свободного падения не следует отдельно анализировать сначала движение вверх, затем вниз: формулы (4.6) – (4.8) описывают все это движение в целом.
· Не всегда удается так подобрать используемые формулы, чтобы ответы получались в одну строчку; приходится составлять и решать систему взаимосвязанных уравнений.
· Если оба корня квадратного уравнения положительны, это не означает, что оба они удовлетворяют условию задачи. Нужно присмотреться к ним внимательнее.
Чудеса зазеркалья
Задача 8. 1*. На расстоянии L от вертикальной стены с высоты H параллельно полу и перпендикулярно стене брошен мяч. Какова должна быть начальная скорость мяча, чтобы после абсолютно упругого удара он коснулся пола на расстоянии от стены большем, чем L?
Как и в предыдущей задаче, мяч можно считать частицей и пренебречь сопротивлением воздуха. Это позволяет выделить две подзадачи: о движении на участке траектории AB и о движении на участке BC (рис. 7). Оба движения происходят с постоянными ускорениями 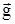, но начинаются в различных точках пространства и с различными скоростями.
Можно записать дополнительные уравнения, связывающие начальные условия выделенных подзадач и решать полученную систему уравнений. Решите задачу, следуя этому плану, самостоятельно. «Не так страшен черт, как его малюют». Этим займетесь позже, а сейчас поищем обходные пути, ведущие к более рациональному способу решения. Для этого подумаем, что можно извлечь из содержащегося в условии указания на «абсолютно упругий удар».
Опыт игры с мячом у стены и наблюдение за движением биллиардных шаров позволяет догадаться о смысле этого указания. Имеется в виду неизменность модуля скорости и угла ее наклона к стене при ударе, то есть v1 = v2 = v и a1 = a2 = a (рис. 7). Более обстоятельно содержание понятия «абсолютно упругий удар» и происхождение указанных условий можно выяснить, анализируя удар с помощью законов изменения механической энергии и импульса.
Условие, связывающие скорости 1 и 2 при абсолютно упругом ударе означает, что геометрический вектор 2 зеркально симметричен вектору 1 относительно плоскости стены (рис.7). Нельзя ли воспользоваться этой симметрией для упрощения решения задачи?
Попытаемся рассмотреть более простую задачу, изменив условие. По какой траектории двигался бы мяч, если бы не было стены? По параболе ABD. Чем отличается участок траектории BD от участка BC? Кажется, он зеркально симметричен BC. Докажем (или опровергнем) это предположение.
Симметрия этих участков будет доказана, если выяснится, что за одно и то же время в обоих случаях мяч опускается на одну и ту же величину вниз, удаляясь от плоскости стены на одинаковые расстояния, но в противоположные стороны. Применяя формулу (4.6), найдем для перемещений за время t:
– проекция на ось y (рис. 7) перемещения вдоль BD равна
v1 t cos a1+ g t2 / 2 = v t cos a + g t2 / 2;
– проекция на ту же ось перемещения вдоль BC равна
v2 t cos a2+ g t2 / 2 = v t cos a + g t2 / 2;
– проекция на ось x (рис. 7) перемещения вдоль BD равна
v1 t sin a1 = v t sin a;
– проекция на ту же ось перемещения вдоль BC равна
– v2 t sin a2 = – v t sin a.
Сравнивая эти выражения, убеждаемся в справедливости высказанного предположения о симметрии траекторий движения по участкам BD и BC.
Как можно использовать эту симметрию? Можно истинное движение (по участку BC) заменить движением «в зазеркалье» (по участку BD). Что за движение на всем пути ABD получится при такой замене? Получится такое же движение мяча, как и в отсутствии стены. Задача свелась к более простой задаче, эквивалентной заданной: с какой скоростью v нужно бросить мяч в горизонтальном направлении на высоте H, чтобы он удалится в этом направлении дальше, чем 2 L.
Чтобы решить полученную более простую задачу, достаточно применить уравнение (4.6) для перемещения (см. рис. 7) в проекции на ось x и на ось y:
SX = v0 t > 2 L; (8.1)
SY = H = g t2 / 2. (8.2)
Исключая время t, получим
t = 
Þ v0 > L 
(8.3)
В копилку опыта
· 
«Зазеркалье» позволило чудесным образом превратить громоздкую и «страшную» задачу в простую и «симпатичную». Использование зеркальной (в общем случае физической симметрии) – эффективное средство упрощения многих задач.
