Осипова Л.М.
«Содержание образования является одним из факторов экономического и социального прогресса общества должно быть ориентировано на: обеспечение самоопределения личности, создания условий для ее самореализации; развитие общества; укрепление и совершенствование правового государства». Статья 14 (пункт 1) Закона об образовании Российской Федерации
Целью современного образования является полное достижение развития тех способностей личности, которые нужны ей и обществу. Поэтому образование в настоящее время характеризуется усилением внимания к ученику, к его саморазвитию и самопознанию, к воспитанию умения искать и находить свое место в жизни. В инструктивно-методическом письме Белгородского РИПКиППС «О преподавании математики в 2006/2007 учебном году в общеобразовательных учреждениях Белгородской области» подчеркивается, что математическое образование в системе общего среднего образования занимает одно из ведущих мест. Это определяется безусловной практической значимостью математики, ее возможностями в развитии и формировании мышления человека, ее вкладом в создание представлений о научных методах познания действительности.
Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования. Поэтому создание классов профильного изучения отдельных предметов, в том числе и математики, помогает школам решать вопросы гуманизации и гуманитаризации образовательного процесса. Конечно, математика является главным гуманитарным предметом в школе, потому что именно она развивает универсальные (общие) способности, умения и навыки, являющиеся основой существования человека в социуме.
Достаточное количество часов математики в неделю в классах профильного изучения математики дает возможность изучить ряд тем, выходящих за рамки школьного курса алгебры и начал анализа и геометрии:
v сведения из теории чисел о делимости и сравнении чисел, о решении уравнений выше второй степени в целых числах дают возможность детям успешно справляться с олимпиадными заданиями;
v для доказательства некоторых формул дифференцирования (например, при выводе формулы нахождения производной степенной функции с натуральным показателем), которые в школьном курсе не обосновываются строго, учащиеся используют метод математической индукции;
v чтобы детям было легче и быстрее выполнять расчеты по многочленам, они были ознакомлены со схемой Горнера;
v зная деление многочленов (с использованием теоремы Безу), они научились снижать степень уравнения с одной переменной, раскладывать такой многочлен на множители;
v знание биномиальных коэффициентов позволяет им раскладывать на множители разность n - х степеней двучлена выше 5 – й степени;
v сведения из языка логики дают учащимся возможность более осознанно относиться к математической символике, употребляемой не только в школьных учебниках, но и в дополнительной литературе по предмету при подготовке к выпускным и вступительным экзаменам в ВУЗы;
v вопросы стратегии поиска решения задач на примере решения уравнений и неравенств с модулем позволяет им подготовиться в будущем к решению заданий группы С из тестов за курс средней школы;
v изучение темы «Комплексные числа» формирует у учащихся привычку строго следить за математической речью, то есть они начинают понимать смысл такой фразы: «Уравнение не имеет корней на множестве действительных чисел», ведь теперь они умеют находить все корни, в том числе и комплексные, многочлена n -ой степени.
Одним из плюсов углубленного, предпрофильного и профильного изучения математики является то, что ежегодно эти дети сдают переводной экзамен по алгебре, а в старших классах по алгебре и началам анализа, причем в форме тестирования. Кроме того, за курс основной школы одним из предметов по выбору для сдачи экзамена в этих классах является геометрия, поэтому им легче усваивать курс стереометрии в старших классах.
Все это позволяет обучающимся успешно выступать на олимпиадах, сдавать экзамены как выпускные, так и вступительные, не бояться приступать к решению задач В-10, В-11 из КИМов для итогового тестирования, добиваться неплохих результатов при участии в различных конкурсах, в том числе, и международных. Второй год подряд дети выполняют задания конкурса «Кенгуру», трое из них имеют дипломы. Одна из учениц класса с профильным изучением математики за работу « Применение стереометрического и планиметрического материала к решению задач с сельскохозяйственным содержанием» получила на Втором Всероссийском соревновании молодых исследователей диплом за лучшую исследовательскую работу в номинации «Прикладная математика и математическое моделирование».
Очень важным аспектом является изучение в школе некоторых тем из курса математики ВУЗов, конечно, на доступном для детей уровне, но и достаточно научном, что способствует более быстрой адаптации школьников при дальнейшем обучении. Так, тема «Многочлены с несколькими переменными» – подготавливает к изучению раздела математического анализа «Функции многих переменных, «Сравнения» - к изучению теории чисел, «Декартовы координаты на плоскости» - очень важно для изучения аналитической геометрии, «Немного о пределах» - позволяет подготовить обучающихся к изучению первой темы математического анализа. Знание о «Треугольнике Паскаля» (о биномиальных коэффициентах) помогает формировать у обучающихся навыки возведения двучлена в любую степень.
Педагогическая проблема обучения математике в средних и старших классах во многом сводится к тому, чтобы поддержать и развить мотивационную сторону.
Чтобы подготовить детей психологически к изучению темы, выходящей за школьный курс математики, очень часто приходится «перешагнуть через порог университета»:
Ø Изучение каждой новой темы в курсе математики желательно начинать с мотивации. На уроке алгебры в 8 классе (классе с углубленным изучением математики) после сообщения темы урока «Преобразование дробных выражений» детям можно рассказывать, что сегодня они научатся представлять дробь 
(1)в виде суммы дробей 
. Затем учащимся предлагается прочитать фрагмент темы «Интегрирование рациональных функций» из «Справочника по высшей математики» М.Я.Выгодского, конечно, не углубляясь в понятие интеграла. И дети видят, что такие преобразования дробей нужно выполнить, чтобы найти интеграл дроби вида (1).
Ø Или при изучении, например, темы «Неравенства-следствия, равносильные неравенства». Чтобы заинтересовать учащихся этим вопросом, можно рассказать им об использовании неравенств вида ах+ву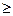 
с и ах+ву 
с в задачах экономического характера. Допустим, какое-то сельскохозяйственное объединение хочет закупить грузовые машины двух типов, учитывая при этом выделенную для этой цели сумму денег, расход горючего и общую грузоподъемность этих машин. Получается система трех неравенств вышеуказанного вида. Если ее решение изобразить множествами на координатной плоскости, то внутри полученного треугольника будет заключена лишь одна точка с натуральными координатами (к примеру (4;5)). И это будет означать, что целесообразнее купить 4 машины одной грузоподъемности и 5 машин другой грузоподъемности.
При изучении темы «Среднее взвешенное и его свойства» из элективного курса «Замечательные неравенства: способы получения и примеры применения» в старших классах можно привести пример, что в одном из своих телевизионных выступлений президент России В.В.Путин упоминает об использовании среднего взвешенного при формировании цен на нефть.
Все это способствует формированию у детей желания получить высшее образование, пониманию ими того факта, что знания никогда не бывают лишними. Чем шире кругозор и глубже знания, тем успешнее будет как сдача выпускных и вступительных экзаменов, так и дальнейшее обучение в колледже или ВУЗе.
Но есть и минус в создании классов профильного изучения отдельных предметов. Кто-то из великих мыслителей сказал: «Хочешь изучить предмет – начни его преподавать». В общеобразовательных классах, где были дети самых различных уровней обучаемости, всегда более способные ученики помогали своим товарищам, работая в парах и группах, приобретая навыки преподавательской деятельности, умение работать в коллективе, учатся быть толерантными. Может быть, поэтому в каждом из выпусков ученики выбирают профессию учителя математики. Их выбор обусловлен тем, что они имеют и знания, и представление о своей будущей специальности. А сейчас, наверное, в каждой школе есть класс, где собраны дети с низким уровнем учебной мотивации и обучаемости. И очень часто родители боятся таких классов как огня, интуитивно ощущая, что ребенку там не на кого будет опереться в трудную минуту. Но в нашей школе такие дети имеют возможность получить рабочую профессию на базе МОУ «Верхопенская СОШ», что в какой – то мере компенсирует их недостатки при изучении более трудных предметов, формирует у них самоуважение, уверенность в завтрашнем дне, в возможности заработать своим трудом средства на дальнейшее обучение. Но, наверное, есть еще какие – то решения проблем, возникающих при организации классов с профильным изучением отдельных предметов. Очень хотелось бы услышать или прочитать о них.
