Рассмотрим дифференцируемую на множестве 
функцию 
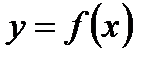и её производную 
. Производная является в свою очередь некоторой функцией аргумента 
. Если производная – дифференцируемая функция на множестве , то по отношению к ней снова можно ставить вопрос о нахождении производной. Назовем 
производной первого порядка или первой производной.
Производную от производной функции 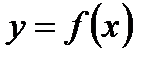называют производной второго порядка или второй производной и обозначают так: 
, или 
, или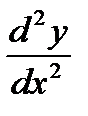 
.
Производная от второй производной называется производной третьего порядка или третьей производной и т.д.
Аналогично производной n-ого порядка от функции 
называется производная от производной (n-1)-ого порядка, т.е.
Обозначается n-ая производная так: 
, или 
, или
Производные, начиная со второй, называются производными высших порядков. Все они получаются последовательным дифференцированием данной функции.
Пример 1. Найти производные второго порядка от функций
1. 
.
2. 
.
Решение.
1. 
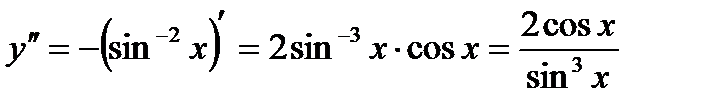
2. 
Пример 2. Найти 
, если 
.
Решение.
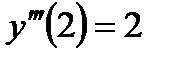
Применение производной. Правило Лопиталя.
Способ раскрытия неопределенностей вида 
или 
при помощи производных называют обычно «правилом Лопиталя» (Лопиталь Гильом Франсуа (1661-1704 гг.) – французский математик).
Теорема. Пусть функции 
и 
дифференцируемы в некоторой окрестности точки 
, кроме, может быть, самой точки , и пусть 
в этой окрестности. Если 
или 
, и при этом существует предел (конечный или бесконечный) отношения производных 
при 
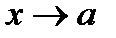, то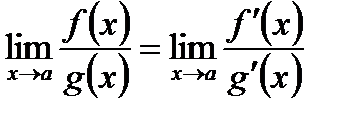 
.
Итак, правило Лопиталя утверждает, что предел отношения бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует.
Эта теорема справедлива также для односторонних пределов и в случае, когда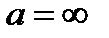 
, 
.
Таки образом, непосредственно правило Лопиталя используется лишь при раскрытии неопределенностей вида или . Тем не менее, к этому виду неопределенностей можно сводить неопределенности других видов.
Пример 1. Найти 
.
Решение. Если в заданное отношение подставим 
, то получим неопределенность вида . Применим правило Лопиталя.
.
Пример 2. Найти 
.
Решение. Имеем неопределенность вида 
. Применим правило Лопиталя.
.
Заметим, что применять правило Лопиталя можно неоднократно. Следует так же комбинировать правило Лопиталя с любыми другими приемами вычисления пределов. В случае неоднократного применения правила Лопиталя следует выполнить все возможные упрощения в выражении, полученном на предыдущем шаге.
Пример 3. Найти 
.
Решение. 
.
Пример 4. Найти 
.
Решение. Имеем неопределенность вида 
.
.
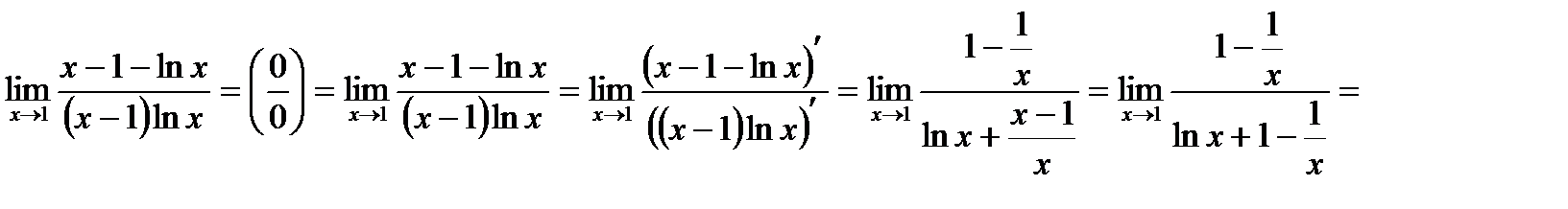
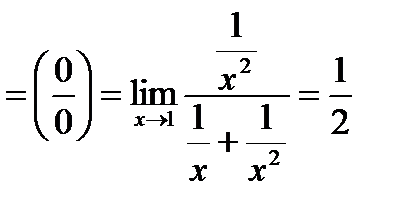