Числовой последовательностью называется числовая функция  , заданная на множестве натуральных чисел. Будем называть числовую последовательность просто последовательность. Обозначают ее так:
, заданная на множестве натуральных чисел. Будем называть числовую последовательность просто последовательность. Обозначают ее так: 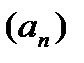 ,
,  ,
,  ,
,  ,
,  и т.д. Индекс
и т.д. Индекс 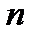 указывает на значение аргумента,
указывает на значение аргумента,  - значение функции (
- значение функции ( ).
).
Примеры последовательностей.
1)  .
.  .
.  - члены последовательности;
- члены последовательности;  -
-  член последовательности.
член последовательности.
2)  .
. 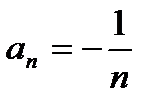 . Подробная запись этой последовательности выглядит так:
. Подробная запись этой последовательности выглядит так:
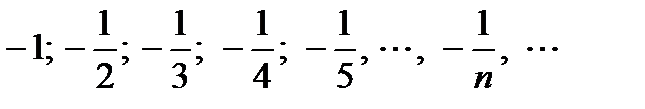
Короткая запись этой последовательности  . Можно найти любой член этой последовательности, зная
. Можно найти любой член этой последовательности, зная  . Например,
. Например,  ,
,  .
.
3) 
Для последовательности можно рассматривать понятие монотонности (как частного случая монотонной функции), но нельзя рассматривать четность и периодичность, так как  .
.
Числовая последовательность  называется невозрастающей (неубывающей), если для любого номера п справедливо неравенство
называется невозрастающей (неубывающей), если для любого номера п справедливо неравенство  . Если
. Если 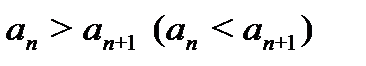 , то последовательность
, то последовательность  - убывающая (возрастающая). Невозрастающие и неубывающие последовательности называются монотонными.
- убывающая (возрастающая). Невозрастающие и неубывающие последовательности называются монотонными.
Геометрически последовательность можно изобразить двумя способами: 1) как функцию графиком на плоскости и 2) точками на прямой.

|
|

|

|
|
 получим
получим
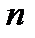
|
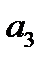
|

|

|

|
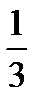
|

|

Данная последовательность  является строго убывающей.
является строго убывающей.
Заметим, что при увеличении номера 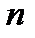 член последовательности
член последовательности  приближается к числу 0, то есть расстояние от
приближается к числу 0, то есть расстояние от  до 0 становится меньше любого задуманного положительного числа
до 0 становится меньше любого задуманного положительного числа 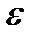 . Таким образом, при
. Таким образом, при 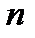 , стремящемся к
, стремящемся к  , член последовательности
, член последовательности  стремится к 0. Дадим строгое определение этому понятию.
стремится к 0. Дадим строгое определение этому понятию.
Число 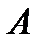 называется пределом последовательности
называется пределом последовательности  , если для любого
, если для любого 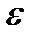
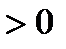 существует число
существует число  , что для всех натуральных чисел
, что для всех натуральных чисел  выполняется неравенство
выполняется неравенство 
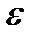 или по-другому: из
или по-другому: из 
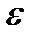

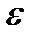
Смысл предела 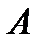 состоит в том, что при номерах
состоит в том, что при номерах 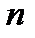 , достаточно больших
, достаточно больших  , члены последовательности
, члены последовательности  близки к
близки к 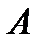 , а именно
, а именно 
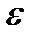 , где
, где 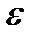
 - любое число и, следовательно,
- любое число и, следовательно, 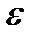 можно взять сколь угодно малым (тогда
можно взять сколь угодно малым (тогда  сколь угодно близко к
сколь угодно близко к 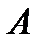 ).
).
Обозначают предел следующим образом:
 или
или  при
при  .
.
Пример. Покажем по определению, что  . Берем любое
. Берем любое 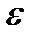
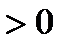 . Рассмотрим неравенство
. Рассмотрим неравенство 
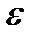 . В данном примере
. В данном примере 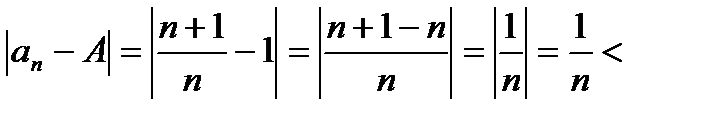
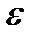 . Неравенство
. Неравенство 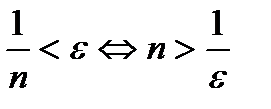 . В качестве
. В качестве  возьмем
возьмем  . (Если взять
. (Если взять  - целая часть
- целая часть  , то
, то  будет целым числом). Тогда получим заключение: для любого
будет целым числом). Тогда получим заключение: для любого  существует
существует  такое, что из
такое, что из  , что означает
, что означает  .
.
 , если для любого
, если для любого  существует
существует  такое, что для всех натуральных
такое, что для всех натуральных 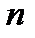 из
из  .
.
Смысл состоит в том, что при 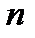 , достаточно больших,
, достаточно больших,  становится больше любого как угодно большого положительного числа
становится больше любого как угодно большого положительного числа  .
.
 , если для любого
, если для любого 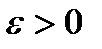 существует
существует  такое, что для всех
такое, что для всех  из
из  .
.
Смысл состоит в том, что  меньше отрицательного как угодно большого по абсолютной величине числа
меньше отрицательного как угодно большого по абсолютной величине числа  при достаточно больших номерах
при достаточно больших номерах 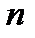 , то есть члены последовательности
, то есть члены последовательности  расположены на оси как угодно далеко влево, если
расположены на оси как угодно далеко влево, если 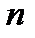 - большие номера.
- большие номера.
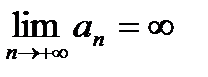 , если для любого числа
, если для любого числа  существует число
существует число  такое, что для всех
такое, что для всех  из
из  .
.
Смысл состоит в том, что  отстоят далеко влево или далеко вправо от нуля на оси, если номера
отстоят далеко влево или далеко вправо от нуля на оси, если номера 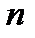 - достаточно большие.
- достаточно большие.
Примеры.
1) 
2) 
3) 
Последовательность  называется сходящейся, если она имеет конечный предел
называется сходящейся, если она имеет конечный предел  . Тогда говорят, что
. Тогда говорят, что  сходится к числу
сходится к числу  , и пишут
, и пишут  при
при 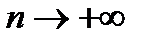 . В противном случае
. В противном случае  называется расходящейся.
называется расходящейся.
Заметим, что  расходится, если
расходится, если  , или
, или  или
или 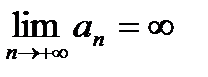 либо, если
либо, если  не существует совсем.
не существует совсем.
Примеры.
1) 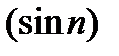 не имеет предела
не имеет предела
2) 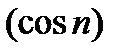 не имеет предела, так как
не имеет предела, так как  не может стремиться ни к какому числу (в силу периодичности
не может стремиться ни к какому числу (в силу периодичности 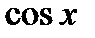 ), и в силу ограниченности, не может стремиться к
), и в силу ограниченности, не может стремиться к  или
или  .
.
Последовательность 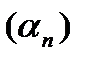 называется бесконечно малой (б/м), если
называется бесконечно малой (б/м), если  или, если для любого
или, если для любого  существует
существует  такое, что для всех
такое, что для всех  из
из  .
.
Последовательность  называется бесконечно большой (б/б), если
называется бесконечно большой (б/б), если  или для любого
или для любого  существует
существует  что для всех
что для всех 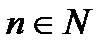 из
из  .
.
Заметим, что из условий  или
или 
 и
и  является бесконечно большой.
является бесконечно большой.
Примеры.
1)  является бесконечно малой
является бесконечно малой
2)  является бесконечно большой
является бесконечно большой
3)  является бесконечно большой, так как
является бесконечно большой, так как  при
при 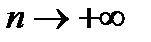 .
.






