1) ѕроизводна€ неопределенного интеграла равна подынтегральной функции.

2) ƒифференциал неопределенного интеграла равен подынтегральному выражению.

3) Ќеопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольна€ посто€нна€.

—войства 1) и 2) используют обычно дл€ проверки результатов интегрировани€.
4) ѕосто€нный множитель можно выносить за знак интеграла, т. е. если  , то
, то

5) Ќеопределенный интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме интегралов от этих функций в отдельности, т. е.
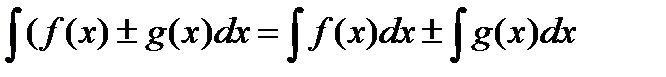 .
.
“аблица основных интегралов.
»з определени€ неопределенного интеграла следует, что если  то
то  . »сход€ из этого и использу€ формулы дифференцировани€, можно составить следующую таблицу неопределенных интегралов.
. »сход€ из этого и использу€ формулы дифференцировани€, можно составить следующую таблицу неопределенных интегралов.
1. 
2. 

3.  ,
, 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 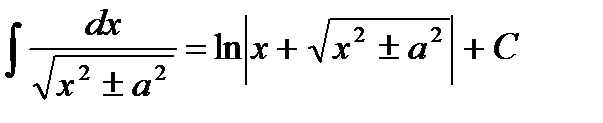 .
.
ѕример 1. Ќайти 
ѕрименив свойства 4) и 5) и табличные интегралы 1,2 и 8, находим

 .
.
ѕример 2. Ќайти  .
.
–аскрыва€ скобки и примен€€ табличные интегралы 4 и 8, найдем
 .
.
»нтегрирование методом замены переменной (методом подстановки).
¬ычислить заданный интеграл непосредственным интегрированием удаетс€ далеко не всегда, а иногда это св€зано с большими трудност€ми. ¬ этих случа€х примен€ют другие приемы. ќдним из наиболее эффективных приемов €вл€етс€ метод подстановки или замены переменной интегрировани€. —ущность этого метода заключаетс€ в том, что путем введени€ новой переменной интегрировани€ удаетс€ свести заданный интеграл к новому интегралу, который сравнительно легко беретс€ непосредственно. –ассмотрим этот метод.
ѕусть функци€  непрерывна на промежутке
непрерывна на промежутке  и
и  , где функци€
, где функци€  непрерывно дифференцируема на промежутке
непрерывно дифференцируема на промежутке  и имеет область значений
и имеет область значений  . ѕусть также функци€
. ѕусть также функци€  имеет обратную
имеет обратную  ,
,  . “огда
. “огда
 .
.
ѕосле вычислени€ интеграла в правой части следует вернутьс€ к старой переменной  , то есть вместо новой переменной
, то есть вместо новой переменной  подставить его значение
подставить его значение  .
.
≈сли интеграл имеет вид  , то его вычисление можно проводить следующим образом:
, то его вычисление можно проводить следующим образом:
 .
.
ѕример.  .
.
–ешение.

ѕример.  .
.
–ешение.

»нтегрирование по част€м.
ѕусть функции  и
и  имеют непрерывные производные на некотором промежутке
имеют непрерывные производные на некотором промежутке  . Ќайдем дифференциал произведени€ этих функций:
. Ќайдем дифференциал произведени€ этих функций:

“ак как по условию функции  и
и  непрерывны, можно проинтегрировать обе части этого равенства,
непрерывны, можно проинтегрировать обе части этого равенства,

или

Ќо  следовательно,
следовательно,
 (1)
(1)
¬ правой части формулы (1) посто€нную интегрировани€ — не пишут, так как она фактически присутствует в интеграле  ‘ормула (1) называетс€ формулой интегрировани€ по част€м.
‘ормула (1) называетс€ формулой интегрировани€ по част€м.
—ущность метода интегрировани€ по част€м вполне соответствует его названию. ƒело в том, что при вычислении интеграла этим методом подынтегральное выражение  представл€етс€ в виде произведени€ множителей
представл€етс€ в виде произведени€ множителей  и
и  ; при этом
; при этом  об€зательно входит в
об€зательно входит в  . ¬ результате получаетс€, что заданный интеграл наход€т по част€м: сначала наход€т
. ¬ результате получаетс€, что заданный интеграл наход€т по част€м: сначала наход€т  а затем
а затем  ≈стественно, что этот метод применим лишь в случае, если задача нахождени€ указанных двух интегралов более проста, чем нахождение заданного интеграла.
≈стественно, что этот метод применим лишь в случае, если задача нахождени€ указанных двух интегралов более проста, чем нахождение заданного интеграла.
|
|
|
ѕример. Ќайти 

ѕри вычислении интегралов методом интегрировани€ по част€м главным €вл€етс€ разумное разбиение подынтегрального выражени€ на множители  и
и  . ќбщих установок по этому вопросу не имеетс€. ќднако дл€ некоторых типов интегралов, вычисл€емых методом интегрировани€ по част€м, сделать это возможно.
. ќбщих установок по этому вопросу не имеетс€. ќднако дл€ некоторых типов интегралов, вычисл€емых методом интегрировани€ по част€м, сделать это возможно.
1. ¬ интегралах вида



где  - многочлен относительно
- многочлен относительно  ,
,  - некоторое число, полагают
- некоторое число, полагают  а все остальные сомножители за
а все остальные сомножители за 
ѕример 2. Ќайти 

2. ¬ интегралах вида





полагают  а остальные сомножители Ц за
а остальные сомножители Ц за 
ѕример 3. Ќайти 

3. ¬ интегралах вида


где  и
и  - числа, за
- числа, за  можно прин€ть любую из функций
можно прин€ть любую из функций  или
или  (или
(или  ). ќднако метод интегрировани€ по част€м придетс€ примен€ть дважды, выбира€ оба раза за
). ќднако метод интегрировани€ по част€м придетс€ примен€ть дважды, выбира€ оба раза за  одну и ту же функцию
одну и ту же функцию  или тригонометрические функции
или тригонометрические функции  ,
,  . ¬ результате двукратного применени€ формулы (1) в правой части равенства по€витс€ искомый интеграл, который находитс€ путем решени€ простого алгебраического уравнени€.
. ¬ результате двукратного применени€ формулы (1) в правой части равенства по€витс€ искомый интеграл, который находитс€ путем решени€ простого алгебраического уравнени€.
ѕример 4. Ќайти 

“ак как в правой части стоит искомый интеграл, то, перенес€ его в левую часть, получим
 .
.
ќтсюда получаем окончательный результат:
 .
.
ќпределенный интеграл.
ѕусть функци€  определена и непрерывна на отрезке
определена и непрерывна на отрезке  . ¬ плоскости ’ќ” дана криволинейна€ трапеци€ ABCD, ограниченна€ отрезком
. ¬ плоскости ’ќ” дана криволинейна€ трапеци€ ABCD, ограниченна€ отрезком  , осью ќ’, пр€мыми
, осью ќ’, пр€мыми  ,
,  и графиком функции
и графиком функции  . “ребуетс€ определить площадь
. “ребуетс€ определить площадь  этой криволинейной трапеции. ƒл€ решени€ этой задачи поступаем следующим образом. –азобьем отрезок
этой криволинейной трапеции. ƒл€ решени€ этой задачи поступаем следующим образом. –азобьем отрезок  оси ќ’ на
оси ќ’ на  элементарных отрезков точками
элементарных отрезков точками 
(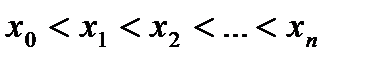 ). „ерез точки делени€ проведем вертикальные пр€мые. ѕри этом криволинейна€ трапеци€ ABCD разобьетс€ на
). „ерез точки делени€ проведем вертикальные пр€мые. ѕри этом криволинейна€ трапеци€ ABCD разобьетс€ на  криволинейных трапеций с основани€ми
криволинейных трапеций с основани€ми  ,
,  ,
,  ,
,  . ¬ каждом из отрезков
. ¬ каждом из отрезков  ,
,  зафиксируем произвольную точку
зафиксируем произвольную точку  (
( ) и построим пр€моугольник с основанием
) и построим пр€моугольник с основанием  и высотой
и высотой  . ≈го площадь равна
. ≈го площадь равна  , где
, где  .
.

–ассмотрим ступенчатую фигуру, составленную из пр€моугольников с основани€ми  ,
,  . ≈е площадь
. ≈е площадь  приближенно равна площади
приближенно равна площади  криволинейной трапеции ABCD
криволинейной трапеции ABCD  . —умма
. —умма  называетс€ интегральной суммой дл€ функции
называетс€ интегральной суммой дл€ функции  .
.
«а площадь криволинейной трапеции естественно прин€ть предел, к которому стрем€тс€ площади построенных указанным образом ступенчатых фигур при неограниченном уменьшении наибольшей длины элементарных отрезков ( ) и, соответственно, неограниченном увеличении числа этих отрезков (
) и, соответственно, неограниченном увеличении числа этих отрезков ( ):
):
 ,
,  ,
,  .
.
ќпределение. ≈сли при неограниченном уменьшении наибольшей длины элементарных отрезков ( ) и соответственно, при неограниченном увеличении числа этих отрезков
) и соответственно, при неограниченном увеличении числа этих отрезков  интегральна€ сумма
интегральна€ сумма  имеет конечный предел, не завис€щий ни от способа разбиени€ отрезка
имеет конечный предел, не завис€щий ни от способа разбиени€ отрезка  на элементарные отрезки, ни от выбора точек
на элементарные отрезки, ни от выбора точек  , ни от способа суммировани€, то такой предел называетс€ определенным интегралом от функции
, ни от способа суммировани€, то такой предел называетс€ определенным интегралом от функции  на отрезке
на отрезке  и обозначаетс€
и обозначаетс€  .
.
»так, по определению
 (1)
(1)
«десь  и
и  соответственно нижний и верхний пределы интегрировани€,
соответственно нижний и верхний пределы интегрировани€,  - независима€ переменна€,
- независима€ переменна€,  - подынтегральна€ функци€,
- подынтегральна€ функци€,  - подынтегральное выражение.
- подынтегральное выражение.
«аметим без доказательства, что если подынтегральна€ функци€  непрерывна на отрезке
непрерывна на отрезке  , то определенный интеграл от этой функции на
, то определенный интеграл от этой функции на  существует.
существует.
ќпределение. ‘ункци€  называетс€ интегрируемой на отрезке
называетс€ интегрируемой на отрезке  , если интеграл от этой функции на
, если интеграл от этой функции на  существует.
существует.
≈сли интегрируема€ на отрезке  функци€
функци€  неотрицательна, то определенный интеграл
неотрицательна, то определенный интеграл  численно равен площади S криволинейной трапеции, ограниченной графиком функции
численно равен площади S криволинейной трапеции, ограниченной графиком функции  , осью абсцисс и пр€мыми
, осью абсцисс и пр€мыми  и
и  (см. рис. 2), т. е.
(см. рис. 2), т. е.  (2)
(2)
|
|
|

–ис. 2
¬ этом заключаетс€ геометрический смысл определенного интеграла.
≈сли во всех точках отрезка  функци€
функци€  неположительна, т.е.
неположительна, т.е.  дл€
дл€  , то права€ часть в формуле (1) также определ€ет площадь соответствующей криволинейной трапеции, но вз€той со знаком Ч, т.е.
, то права€ часть в формуле (1) также определ€ет площадь соответствующей криволинейной трапеции, но вз€той со знаком Ч, т.е.

ѕри введении пон€ти€ определенного интеграла как предела интегральных сумм мы допустили, что  . ¬ случае
. ¬ случае  примем, по определению,
примем, по определению,
 (3)
(3)
ѕри  также по определению, полагаем
также по определению, полагаем
 (4)
(4)
—ледует заметить, что определенный интеграл зависит только от интегрируемой функции  и пределов интегрировани€
и пределов интегрировани€  и
и  , но не от того, какой буквой обозначаетс€ переменна€ интегрировани€. ѕоэтому
, но не от того, какой буквой обозначаетс€ переменна€ интегрировани€. ѕоэтому
 (5)
(5)
и т.д.






