1. Сумма (разность) конечного числа бесконечно малых есть функция бесконечно малая.
2. Произведение бесконечно малой функции при 
на функцию, ограниченную в окрестности точки 
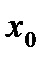, есть функция бесконечно малая.
3. Сумма бесконечно больших функций одного знака является бесконечно большой того же знака.
4. Произведение бесконечно большой при функции на функцию, имеющую предел при , не равный нулю, есть бесконечно большая.
5. Если функция 
является бесконечно малой при , то 
- бесконечно большая, и обратно, если функция является бесконечно большой при , то - бесконечно малая при ,то есть
(символическая запись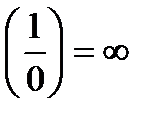 
).
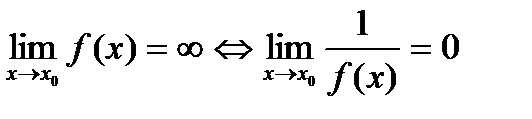(символическая запись 
);
Поведение же функции, являющейся отношением бесконечно малых (неопределенность 
), бесконечно больших 
при ,суммой бесконечно больших разных знаков 
, произведением бесконечно малой на бесконечно большую 
требует исследования. Нахождение предела в случае неопределенности называется раскрытием неопределенности.
Замечательные пределы.
Можно доказать следующие утверждения:
1) 
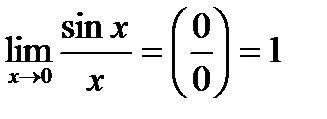
2) 
. Возможно: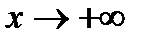 
и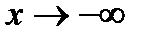 
.
Они называются первым и вторым замечательными пределами.
Справедливы следствия:
1) 
;
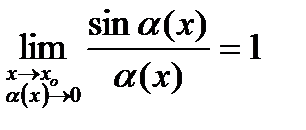2) 
С помощью замечательных пределов расширяется возможность вычислять пределы функций.
Приведем некоторые приемы вычисления пределов, излагая их на конкретных примерах.
Пример. Найти пределы (не применяя правило Лопиталя)
1) 
| 2) 
| 3) 
|
4) 
| 5) 
| 6) 
|
7) 
|
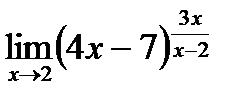
Решение:
1)
Так как пределы числителя и знаменателя при 
равны нулю, то мы имеем неопределенность вида 
. Эту неопределенность можно раскрыть, разложив на множители квадратные трехчлены в числителе и знаменателе и сократив далее на общий множитель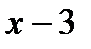 
:
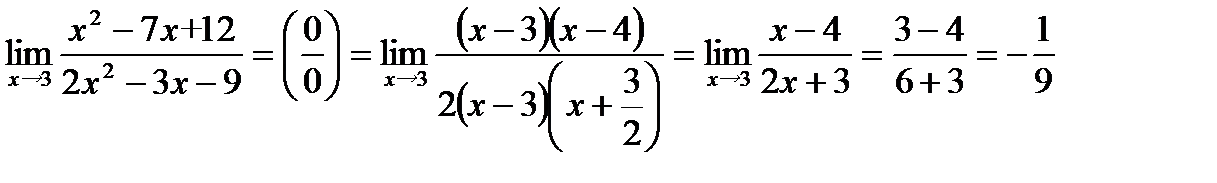
2)
Здесь мы имеем неопределенность вида . Домножим числитель и знаменатель дроби на выражение, сопряженное числителю:
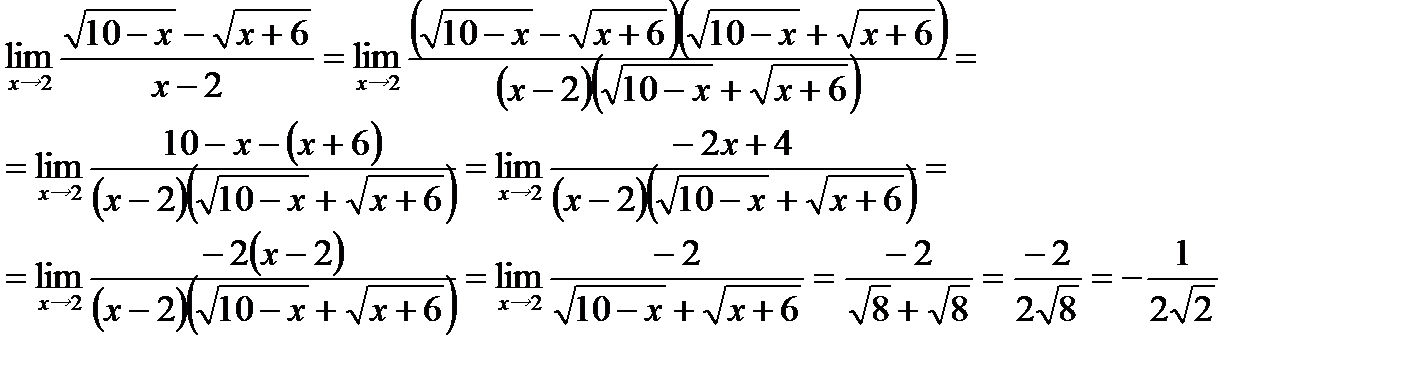
3)
Числитель и знаменатель дроби - бесконечно большие функции, поэтому здесь имеет место неопределенность вида 
. Чтобы раскрыть эту неопределенность поделим числитель и знаменатель на старшую степень переменной х в данной дроби:
.
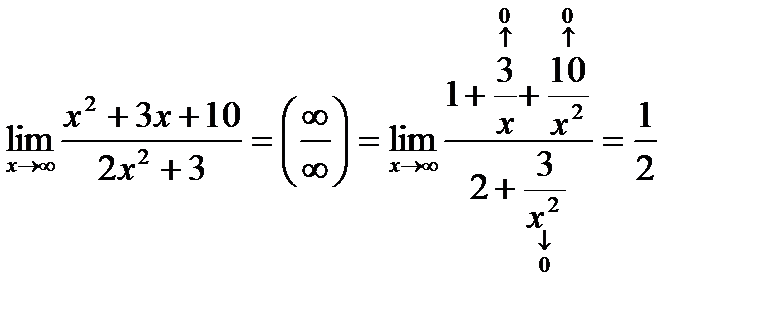4) .
Применяя первый замечательный предел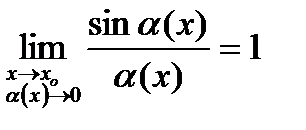 
, получим
.
5) 
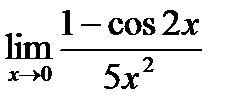
Используя формулу понижения степени 
, преобразуем числитель дроби, затем сведем предел к первому замечательному пределу 
,
.
6) 
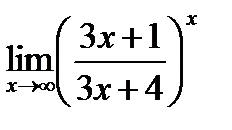
Имеем неопределенность вида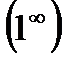 
. Преобразуем функцию так, чтобы воспользоваться вторым замечательным пределом 
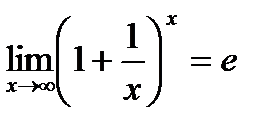, или следствием 
.
7) 
Преобразуем функцию так, чтобы воспользоваться вторым замечательным пределом:
Непрерывность функции.
Функция называется непрерывной в точке 
, если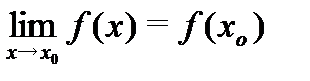 
.
Ищем условия непрерывности в точке 
.
Функция непрерывна в точке , если
1. Существует предел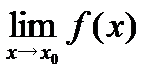 
2. Существует значение функции в точке (
)
3. Этот предел и значение функции совпадают, то есть .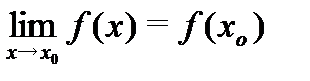
Условие 3 можно переписать в виде: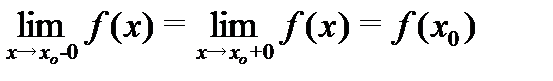 
.
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Если правый (левый) предел совпадает со значением функции, то функция называется непрерывной справа (слева) в рассматриваемой точке, то есть 
Точка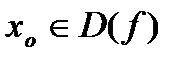 
называется точкой устранимого разрыва, если существуют конечные 
, 
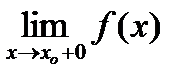и выполняется условие 
.
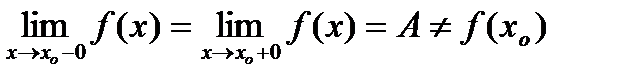Этот разрыв можно устранить, изменив значение функции всего в одной точке, а именно, вместо 
в точке взять значение 
.
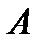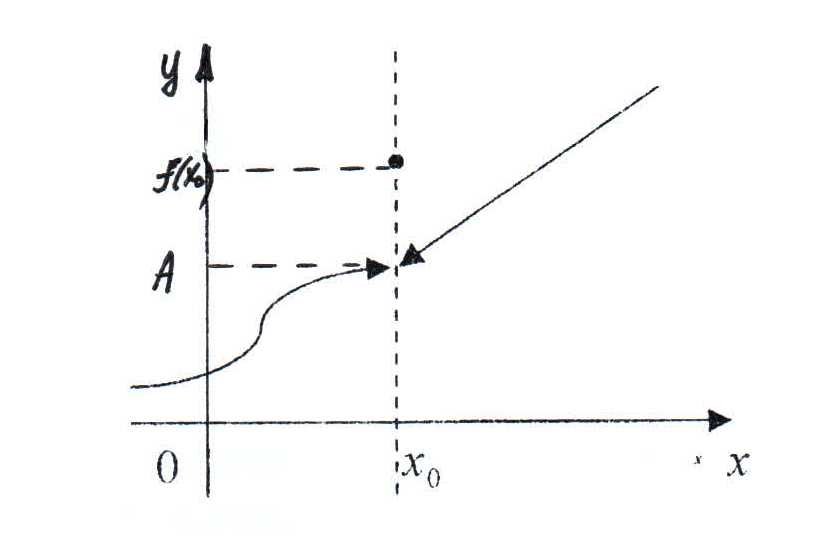
Но это будет уже другая функция, которая будет отличаться от функции 
всего в одной точке (при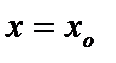 
).
Точка 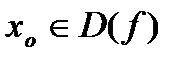называется точкой разрыва I рода с конечным скачком, если существуют конечные 
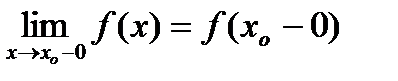и 
, но 
. При этом возможна непрерывность функции, с одной стороны.
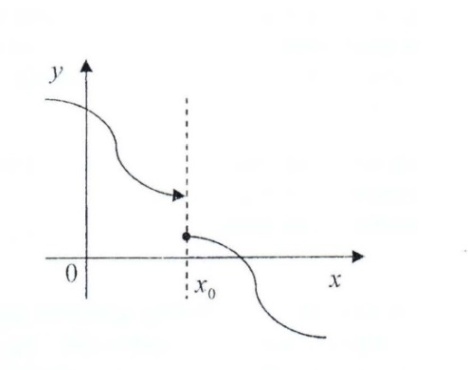
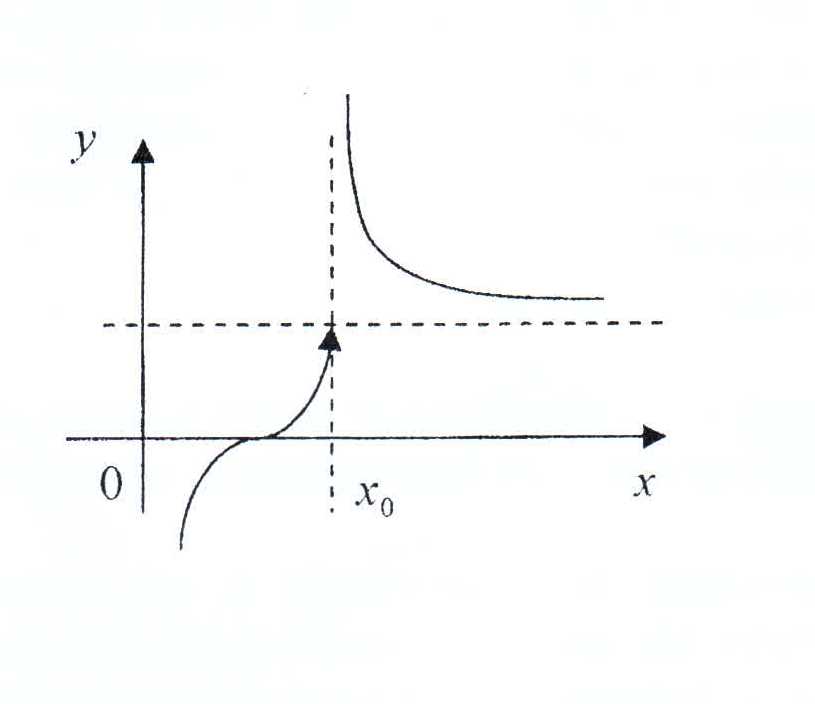
Точка 
называется точкой разрыва II рода, если хотя бы один из односторонних пределов не существует.
Пример. Функция 
задана различными аналитическими выражениями в различных областях изменения независимой переменной. Найти точки разрыва функции, если они существуют, и построить график функции.
Решение. Функции 
, 
, 
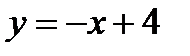являются непрерывными на 
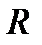. Значит, функция 
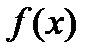может иметь разрыв только в точке перехода от одного аналитического выражения к другому. Такими точками являются точк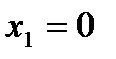и 
и 
. Проверим условие непрерывности для точек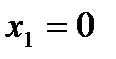 
и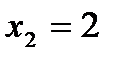 
.
1. Найдем пределы слева и справа в точке 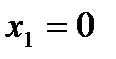и значение функции в этой точке.
.
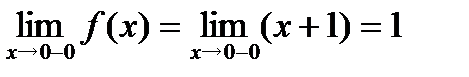
Вывод: так как 
, то функция в точке 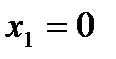является непрерывной.
2. Найдем пределы слева и справа в точке и значение функции в этой точке.
.
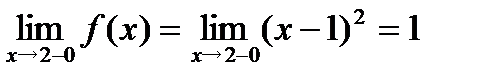
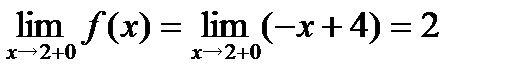
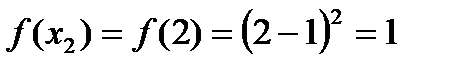Вывод: так как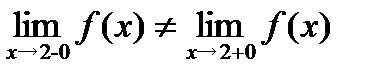 
, то функция в точке 
терпит разрыв. Поскольку односторонние пределы являются конечными, то 
точкой разрыва I рода с конечным скачком (слева непрерывна, так как 
).
Скачок функции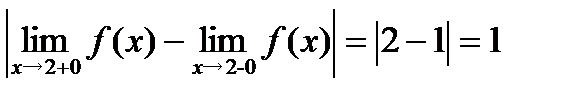 
.
3. Строим график функции
