Исследование функций можно проводить по следующей схеме:
1. Найти область определения функции.
2. Исследовать функцию на четность и нечетность.
3. Найти асимптоты графика функции.
4. Найти интервалы возрастания и убывания функции, её экстремумы.
5. Найти интервалы выпуклости и вогнутости кривой и точки ее перегиба.
6. Найти точки пересечения графика функции с осями координат (если это возможно).
7. Построить график.
Иногда порядок исследования целесообразно выбирать, исходя из конкретных особенностей данной функции.
Пример 1. Построить график функции 
Решение.
1. Область определения функции 
.
2. Функция ни четная, ни нечетная.
3. Выясним вопрос о существовании асимптот. Исследуем поведение функции вблизи точки разрыва 
.
Так как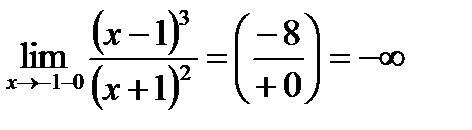 
,
то прямая является вертикальной асимптотой.
Для нахождения наклонных асимптот, вычисляем:
Таким образом, прямая 
наклонная асимптота. Горизонтальных асимптот нет
4. Вычислим производную
Очевидно, что 
при 
и 
. Кроме того, 
не существует при 
, но эта точка не принадлежит области определения функции, следовательно, точка не может быть точкой экстремума.
Методом пробных точек определяем знак производной в каждом из интервалов: 
.
Следовательно, функция возрастает на интервалах 
и убывает на интервале 
.
В точке функция имеет максимум. Так как при переходе через критическую точку производная знака не меняет, то в этой точке экстремума нет.
Имеем, 
.
5. Находим вторую производную
.
при и 
не существует при .
Определяем знак второй производной в каждом из интервалов 
.
График функции выпуклый на интервалах 
и вогнутый на интервале 
.
Точка с абсциссой - точка перегиба, так как при переходе через нее вторая производная меняет знак с минуса на плюс, а график функции изменяет выпуклость на вогнутость.
Имеем 
, следовательно, точка 
является точкой перегиба.
6. Для нахождения точек пересечения графика функции с осями координат полагаем 
, получаем 
. Затем полагаем 
, откуда 
или 
.
Последнее равенство возможно при 
, т.е. при . Других действительных значений, при которых нет, так как для равенства 
имеем дискриминант
.
Таким образом, имеем две точки пересечения графика функции с осями координат: 
и .
7. Построим график данной функции.
РАЗДЕЛ 5. Интегральное исчисление функций одной переменной
Неопределенный интеграл.
Пусть функция 
определена на некотором промежутке 
. Тогда функция 
называется первообразной для функции на промежутке 
, если 
для всех 
.
Если функция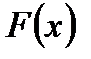 
является первообразной функции на промежутке , то множество всех первообразных для задается формулой 
, где 
- некоторое постоянное число.
Совокупность всех первообразных для функции , определенных на некотором промежутке , называется неопределенным интегралом от функции на этом промежутке и обозначается символом 
.
Если является первообразной для функции на промежутке Х, то 
Функция называется подынтегральной функцией, 
- подынтегральным выражением, 
– переменной интегрирования, символ 
- знаком неопределенного интеграла, С – постоянной интегрирования.
Назовем график какой-либо первообразной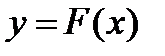 
функции интегральной кривой.
Тогда геометрически неопределенный интеграл представляет собой семейство интегральных кривых, каждая из которых получается из любой другой кривой параллельным переносом вдоль оси Оу.
|
