В науке проблема классификации является одной из самых важных задач. В математике часто встречается разбиение любого множества на классы (подмножества).
В общем случае, разбиение любого множества М на классы B 1, B 2,..., Вn определяется следующими условиями:
1. Bi ≠ Æ для всех i = 1, 2,..., n.
2.  Æ для всех i, j = 1, 2,..., n, где i ≠ j.
Æ для всех i, j = 1, 2,..., n, где i ≠ j.
3.  .
.
Рассмотрим три задачи классификации с помощью одного, двух и трех свойств. Предположим, что имеется множество М и некоторое свойство a, которым могут обладать элементы из М.
Выделить подмножество B из множества М можно, указав одно свойство a, которым обладают некоторые элементы множества М.
 Например, М – множество натуральных чисел от 1 до 100, a – это свойство «быть четным числом». В этом случае множество М разбивается на два непересекающихся подмножества А и В, где множество А состоит из всех элементов множества М, обладающих свойством a, а В состоит из всех элементов множества М, не обладающих свойством a (рис. 11).
Например, М – множество натуральных чисел от 1 до 100, a – это свойство «быть четным числом». В этом случае множество М разбивается на два непересекающихся подмножества А и В, где множество А состоит из всех элементов множества М, обладающих свойством a, а В состоит из всех элементов множества М, не обладающих свойством a (рис. 11).
Очевидно, что  и
и  Æ, так как любой элемент из М либо обладает свойством a, либо не обладает a и не может быть так, что один и тот же элемент одновременно обладает свойством a и не обладает им же.
Æ, так как любой элемент из М либо обладает свойством a, либо не обладает a и не может быть так, что один и тот же элемент одновременно обладает свойством a и не обладает им же.
Предположим теперь, что заданы два свойства a и b, которыми могут обладать или не обладать элементы множества М. Например, М – множество натуральных чисел от 1 до 100, свойство a – это «быть четным числом», свойство b – это «быть числом кратным трем».
Пусть А – множество чисел из М, обладающее свойством a, В – множество чисел из М, обладающее свойством b. Опишем все классы, на которые разбивается множество М с помощью свойств a и b.
Первый класс состоит из всех чисел множества М, обладающих и свойством a и свойством b, то есть из чисел, кратных 6, его можно обозначить  . Второй класс состоит из всех чисел множества М, обладающих свойством a и не обладающих свойством b, то есть из чисел, кратных 2, но не кратных 3, его можно обозначить
. Второй класс состоит из всех чисел множества М, обладающих свойством a и не обладающих свойством b, то есть из чисел, кратных 2, но не кратных 3, его можно обозначить  . Третий класс состоит из всех чисел множества М, не обладающих свойством a и обладающих свойством b, т.е. из нечетных чисел, кратных 3, его можно обозначить
. Третий класс состоит из всех чисел множества М, не обладающих свойством a и обладающих свойством b, т.е. из нечетных чисел, кратных 3, его можно обозначить 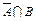 . Четвертый класс состоит из всех чисел множества М, не обладающих свойством a и не обладающих свойством b, т.е. из нечетных и не кратных трем чисел. Его можно обозначить
. Четвертый класс состоит из всех чисел множества М, не обладающих свойством a и не обладающих свойством b, т.е. из нечетных и не кратных трем чисел. Его можно обозначить  . Описанный случай изображен на рис. 12.
. Описанный случай изображен на рис. 12.
 В рассмотренном случае при разбиении множества на классы с помощью двух свойств получилось 4 класса. Так получается не всегда. Читателю предлагается описать все классы, на которые разбивается множество М с помощью
В рассмотренном случае при разбиении множества на классы с помощью двух свойств получилось 4 класса. Так получается не всегда. Читателю предлагается описать все классы, на которые разбивается множество М с помощью
Рис. 12 свойств a и b, если:
а) все элементы, обладающие свойством a, обладают свойством b;
б) не существует элементов, обладающих одновременно свойствами a и b;
в) любой элемент обладает хотя бы одним из свойств a или b (рассмотреть все подслучаи).
Рассмотрим случай, когда заданы три свойства a, b, g. В общем случае разбиение множества М на классы изображено на рис. 13.
 Рис. 13
Рис. 13
| Нетрудно подсчитать, что в этом случае получилось 8 классов. Приведем по порядку их обозначения:
(1)  ; (2) ; (2) 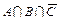 ;
(3) ;
(3) 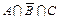 ; (4) ; (4)  ;
(5) ;
(5)  ; (6) ; (6)  ;
(7) ;
(7)  ; (8) ; (8)  . .
|
Читателю предлагается самостоятельно описать подмножества, получающиеся при разбиении множества на классы с помощью свойств a, b, g.
Как видно из приведенных примеров, с помощью одного свойства осуществляется разбиение множества на 2 класса, с помощью двух свойств на 4 класса, с помощью трех свойств на 8 классов. Можно предположить, что с помощью m свойств осуществляется разбиение множества, вообще говоря, на 2 m классов. Эта гипотеза будет доказана в § 4 главы III.
Вопросы и задания для самопроверки
1. Можно ли задать одно и то же множество, указав различные характеристические свойства его элементов?
2. Можно ли задать одно и то же множество перечислением и указав характеристическое свойство?
3. Какие из числовых множеств А, В, С могут быть заданы перечислением всех его элементов:
А = { х | х Î R, –5 £ х < 5}, В = [1, 10], С = { х | х Î N, 1 £ х £ 10}?
Глава II






