Отношения между множествами

Математика ГЛАВА I

МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ

Теория множеств – это фундамент математики как высшей, университетской, так и школьной. Она изучает свойства множеств, операции над множествами, исследованием операций над множествами занимается «алгебра множеств». Под этим термином в современной математике понимают само множество с введенными в нем операциями, обладающими определенными свойствами.

Множество и его элементы

Множество является центральным понятием данной главы. Несмотря на то, что это понятие встречается едва ли не в каждом определении, оно само остается без определения. Множество – это одно из неопределяемых математических понятий. Это понятие можно описать или раскрыть его содержание на примерах. Известно описание понятия множества немецким математиком Георгом Кантором (1845–1918). Он говорил, что «множество – есть многое, мыслимое, как единое целое».

Множество можно представить себе как совокупность (собрание, класс) некоторых предметов, объединенных по какому-либо признаку.

С различными множествами человеку приходилось иметь дело в глубокой древности, когда, еще не существовало понятия «число». Часто в повседневной жизни возникала необходимость сравнивать численность различных совокупностей или объекты одной и той же совокупности в различное время. Например, голов скота столько, сколько зарубок на дереве, или с пастбища возвратилось столько голов скота, сколько ушло на пастбище.

Мы сейчас тоже часто используем понятие множество: говоря «стая» представляем множество птиц, «табун» – множество лошадей, «стадо» –множество коров, «отара» – множество овец.

В математике удобно рассматривать геометрическую фигуру как множество точек, обладающих определенными свойствами; решение уравнения или неравенства – как множество значений переменной, удовлетворяющих данному уравнению или неравенству.

Теория множеств занимается изучением общих свойств множеств, не зависящих от природы объектов, образующих эти множества.

Определение. Предметы (объекты), из которых составлено множество, называют элементами множества.

Множества принято обозначать большими латинскими буквами А, В,..., а его элементы малыми латинскими буквами а, в,... или какой-нибудь, одной буквой с индексом, например, а ₁, а ₂, а ₃,.... Если а является элементом множества А, то символически записывают 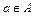, читают «а принадлежит множеству А» или «а является элементом А». Если а не принадлежит множеству А, то символически записывают .

Само понятие «множество» наводит на мысль, что каждое множество должно содержать много элементов. В повседневной жизни один предмет или совокупность двух предметов обычно не называют множеством. Никто не говорит, что у человека множество рук или ног, хотя говорят о множестве волос на голове или о множестве кровеносных сосудов.

В математике же для общности рассуждений удобно считать множеством совокупность любого числа элементов. Рассматривают множества, содержащие только один элемент (одноэлементное множество), и даже множество, не имеющее ни одного элемента.

Определение. Множество, которое не содержит элементов, называют пустым и обозначают символом Æ.

Множество, число элементов которого может быть выражено некоторым натуральным числом, называется конечным. Например: множество дней недели.

Введение одноэлементных множеств и пустого множества позволяет, например, утверждать, что всякое уравнение имеет множество решений, число элементов последнего множества зависит от вида уравнения и области его задания. Так, для уравнения 15 х – 2 = 0 множество рациональных корней содержит один элемент, для уравнения х + 10 = х – 9 множество решений пусто.

Понятие множества значительно облегчает изучение различных свойств многочисленных объектов в любой отрасли знаний. Невозможно изучить или описать каждое живое существо, обитающее на Земном шаре. Но классификация по признакам, присущим множеству животных того или иного класса, позволяет описать весь животный мир даже в узких рамках учебника зоологии. Невозможно было бы изучить свойства даже плоских фигур, если не выделить свойства, присущие множеству фигур данного типа.

Способы задания множеств

Множество можно считать заданным, если есть способ, позволяющий для любого данного предмета решить, принадлежит он этому множеству или не принадлежит.

Применяется два основных способа задания множеств. Первый способ – перечисление всех его элементов (в произвольном порядке); второй способ – указание характеристического свойства, т.е. такого свойства, которым обладают все элементы этого множества и не обладает ни один предмет, не являющийся его элементом.

Например, множество А = { а, с, d } задано перечислением всех его элементов. Такое множество обозначается посредством фигурных скобок, в которых заключается перечень всех элементов, разделенных запятыми. Совершенно очевидно, что перечислением всех элементов можно задать только конечное множество.

При задании этим способом множества всех двузначных чисел пришлось бы перечислять 90 элементов, а для записи множества всех трехзначных чисел – 900 элементов. Для составления списка всех людей, населяющих в данный момент нашу планету, потребовалось бы достаточно много времени. Составление списка натуральных чисел вообще невозможно, так как он бесконечен. Ясно, что способ перечисления, даже если пренебречь его неудобством в случае очень большого числа элементов, применим не для всех множеств. Чтобы задать конкретное множество, надо указать характеристическое свойство, которым обладают только элементы этого множества.

Зададим, например, множество всех простых чисел с помощью следующего характеристического свойства: этому множеству принадлежат те и только те натуральные числа, которые делятся только на 1 и сами на себя.

Множество элементов, заданных указанием характеристического свойства, записывают так: в фигурных скобках после обозначения элемента множества любой малой буквой латинского алфавита ставится двоеточие или вертикальная черта, а потом указывается характеристическое свойство.

Например, запись А = { х | x Î R и –7 < х < 20} означает, что элементами множества А являются все действительные числа, удовлетворяющие неравенству: –7 < х < 20. Или, говоря о множестве В натуральных четных чисел, мы указываем характеристическое свойство его элементов и записываем так:

В = { х | и х кратно 2}.

Числовые множества

Для математики особую роль играют множества, элементами которых являются математические объекты (числа, точки, уравнения, функции и т.д.).

Множества, элементами которых являются числа, называются числовыми множествами. Для некоторых числовых множеств приняты специальные обозначения:

N – множество натуральных чисел;

N₀ – множество целых неотрицательных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел;

R – множество вещественных (действительных) чисел.

Различные подмножества множества R можно изобразить на координатной прямой. Если а и b – различные действительные числа
(а < b), то запись и изображение на координатной прямой различных числовых множеств будут такими, как в таблице 1.

Таблица 1

Числовое множество	Обозначение	Изображение на координатной прямой
{ x | x Î R, a < x < b }	(a, b)
{ x | x Î R, a £ x £ b }	[ a, b ]
{ x | x Î R, a £ x < b }	[ a, b)
{ x | x Î R, a < x £ b }	(a, b ]
{ x | x Î R, x ³ a }	[ a, +¥)
{ x | x Î R, x > a }	(a, +¥)
{ x | x Î R, x £ a }	(-¥, a ]
{ x | x Î R, x < a }	(-¥, a)

 

Множество действительных чисел R обозначается также
(–¥, +¥) и называется числовой прямой. Всякая координатная прямая является изображением числовой прямой.

Отношения между множествами

Как в практической жизни, так и в теоретических рассуждениях часто приходится выбирать из нескольких множеств элементы и образовывать из них новые множества, устанавливать различные отношения между имеющимися множествами.

Особый интерес представляют отношения между множествами, имеющими одинаковую природу элементов.

I. Отношение нестрогого включения.

Рассмотрим пример. Пусть А – множество всех учащихся данного класа, В – множество учащихся этого класса, которые успевают по всем предметам.

Выясним зависимость между принадлежностью одного и того же элемента множествам А и В.

Известно, что х Î В. Можно ли утверждать, что х Î А? (Да). Может ли быть, что х Î В, но х Ï А? (Нет, не может).

Заметим, что каждый элемент множества В является элементом множества А. В этом случае говорят, что В является подмножеством (частью) множества А.

Определение. Если каждый элемент множества В является элементом множества А, то множество В называют подмножеством множества А. Обозначается это так: В А. (Символ обозначает отношение нестрогого включения).

В этом случае говорят также, что множество В включается в множество А, или множество А включает множество В, а также, что множества А и В находятся в отношении нестрогого включения.

П р и м е р ы.

1) Множество учащихся некоторого класса, изучающих английский язык, является подмножеством множества всех учащихся этого класса;

2) Множество книг по математике в некоторой библиотеке является подмножеством множества книг этой библиотеки;

3) Множество прямоугольников включается в множество параллелограммов.

Чтобы наглядно изображать множества и отношения между множествами рисуют геометрические фигуры, которые находятся между собой в этих отношениях.

Изображение множеств с помощью множеств точек плоскости, ограниченных замкнутыми кривыми, называется диаграммой Эйлера-Венна[1]. На рис. 1 дана диаграмма Эйлера-Венна для случая, когда
В А.

А

В

 

Рис. 1

Свойства отношения нестрогого включения.

1°. Всякое множество А есть подмножество самого себя т.е. для всякого А верно А А.

2°. Для любых множеств А, В, С, если А В и В С, то А С. Очевидно, что часть части данного множества всегда является его частью.

3°. Пустое множество считается подмножеством любого множества А:

Æ А.

II. Отношение равенства.

Отношение равенства является частным случаем нестрогого включения.

Определение. Множества А и В, состоящие из одних и тех же элементов, называют равными.

Равенство множеств обозначают так: А = В. Из определения равенства множеств следует, что важен лишь состав множества, и не существенен порядок следования элементов множества.

Например, множества А = { а, в, с }, В = { в, а, с }, С = { с, а, в } равны между собой.

П р и м е р ы.

1) А = {1, 2², 3², 4²} и В = {1, , , }.

Эти множества равны, т. к. они состоят из чисел 1, 4, 9, 16.

2) А – множество ромбов с прямыми углами;

В – множество квадратов. А = В.

Равенство множеств характеризуется тремя свойствами (этими свойствами обладает и отношение равенства чисел).

1°. Для всякого множества А справедливо А = А.

2°. Для любых двух множеств А, В, если А = В, то В = А.

3°. Для любых 3-х множеств А, В, С, если А = В и В = С, то А = С.

Заметим, что очевидно А = В тогда и только тогда, когда и .

III. Отношение строгого включения.

Если в отношении «множество В является подмножеством множества А» () хотят подчеркнуть, что А содержит и другие элементы, кроме элементов из В, то говорят, что В строго включено в А или является правильной частью множества А.

Определение. Если каждый элемент множества В является элементом множества А, и в А существует хотя бы один элемент не принадлежащий множеству В, то множество В строго включается в множество А. Обозначается .

Множество В в этом случае называется собственным подмножеством множества А, т.е. если и .

Так, например, N Ì Z, Z Ì Q, Q Ì R.