Широкое применение отношений эквивалентности в современной математике связано с тем, что всякое отношение эквивалентности осуществляет разбиение множества, в котором оно определено, на классы.
П р и м е р 1. Пусть на множестве всех целых неотрицательных чисел N 0 = {0, 1, 2, 3, …} задано отношение Р: «числа х и у имеют один и тот же остаток при делении на 3». Докажем, что Р – отношение эквивалентности и определим классы эквивалентности, определяемые этим отношением.
В самом деле:
а) отношение Р – рефлексивно, поскольку любое х Î N 0 имеет при делении на 3 тот же остаток, что х;
б) Р – симметрично, поскольку для любых х, у Î N 0, если числа х и у имеют один и тот же остаток при делении на 3, то числа у и х имеют один и и тот же остаток при делении на 3;
в) Р – транзитивно, поскольку для любых трех чисел x, y, z Î N 0, если х и у имеют один и тот же остаток при делении на 3, и у и z имеют один и тот же остаток при делении на 3, то числа х и z имеют один и тот же остаток при делении на 3.
Следовательно, отношение Р: «числа х и у имеют один и тот же остаток при делении на 3» является отношением эквивалентности, и поэтому оно разбивает множество N 0 на классы. Эти классы называются классами вычетов по модулю 3.
[0] – так обозначается класс чисел, дающих при делении на 3 остаток 0, т.е. [0] = {0, 3, 6, 9, 12 …}, или [0] = {3 k }, где k Î N 0.
[1] – так обозначается класс чисел, дающих при делении на 3 остаток 1, т.е. [1] = {1, 4, 7, 10, 13 …}, или [1] = {3 k + 1};
[2] – так обозначается класс чисел, дающих при делении на 3 остаток 2, т.е. [2] = {2, 5, 8, 11, 14 …}, или [2] = {3 k + 2}.
Итак, отношение Р разбивает множество N 0 на 3 класса, и вообще, можно доказать, что отношение «числа х и у имеют один и тот же остаток при делении на m» разбивает это множество на m классов.
П р и м е р 2. На множестве N – натуральных чисел задано отношение Р следующим образом: (х 1, у 1) Р (х 2, у 2)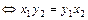 
.
Установим, что Р является отношением эквивалентности и определим классы эквивалентности, определяемые этим отношением.
Действительно, это отношение:
а) рефлексивно, поскольку для любых пар (х, у) имеет место
ху = ух;
б) симметрично, поскольку для любых двух пар натуральных чисел (х 1, у 1) и (х 2, у 2), если х 1 у 2 = у 1 х 2, то х 2 у 1 = у 2 х 1;
в) транзитивно, поскольку для любых трех пар (х 1, у 1), (х 2, у 2), (х 3, у 3), если х 1 у 2 = у 1 х 2 и х 2 у 3 = у 2 х 3, то х 1 у 2 х 2 у 3 = у 1 х 2 у 2 х 3, т.е. х 1 у 3 = у 1 х 3.
Таким образом, отношение Р разбивает множество N на классы эквивалентности. Каждый из этих классов называется рациональным числом.
Например, пары (1, 2), (2, 4), (3, 6) принадлежат одному классу {(1, 2), (2, 4), (3, 6), …}. Можно этот класс определить следующим образом 
, т.е. как множество пар, эквивалентных паре (1, 2). Обычно эти пары записывают так: 
и называют дробями, а эквивалентность пар называют равенством дробей. Для упрощения заменяют класс эквивалентности каким-нибудь его элементом (представителем), чаще всего наиболее простым (несократимой дробью), называя его рациональным числом. Такое упрощение допустимо, так как рациональное число, как класс эквивалентности, однозначно определяется любым элементом этого класса, а операции над рациональными числами, как над классами пар, определяются через операции над представителями этих классов таким образом, что результаты этих операций не зависят от выбора представителей.
Как видно, дробь – форма выражения числа, при этом бесконечное множество дробей, составляющих один класс эквивалентности по отношению P на N, выражает одно число, которое может оказаться целым или дробным положительным числом, т.е. одно рациональное число.
