Любое непустое множество А имеет по крайней мере два подмножества: А и Æ, их называют несобственными подмножествами множества А.
Если А ¹ Æ, то всякий элемент множества А порождает его одноэлементное подмножество, т.е. если 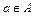 , то { а }
, то { а }  .
.
Множество всех подмножеств множества А обозначают Р (А). Рассмотрим пример. Дано множество А = {1, 2, 3}, составим множество всех его подмножеств Р (А)={ Æ, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}}. Таким образом, данное трехэлементное множество А имеет 8 подмножеств.
Заметим, что пустое множество имеет одно подмножество: Æ.
Итак, Р (А) ≠ Æ, для любого множества А. Для каждого множества, состоящего из m элементов, можно образовать 2 m подмножеств (доказательство этого предложения будет приведено в § 4 главы III пособия).
Нередко бывает так, что в пределах одной задачи рассматривают подмножества одного и того же множества U. Такое множество U называют универсальным множеством.
Так, если А – множество студентов 1-го курса некоторого института, В – множество студенток того же института, С – множество студентов-спортсменов этого института, то в качестве универсального множества U можно взять множество всех студентов данного института, потому что тогда А  U, В
U, В  U, С
U, С  U. На диаграммах Эйлера-Венна универсальное множество U часто изображают в виде прямоугольника, а его подмножества – кругами.
U. На диаграммах Эйлера-Венна универсальное множество U часто изображают в виде прямоугольника, а его подмножества – кругами.
В школьном курсе математики универсальным числовым множеством является множество действительных чисел, в планиметрии – множество точек плоскости, в стереометрии – множество точек пространства. Заметим, что понятие универсального множества относительно. В самом деле, на различных этапах изучения математики в школе в качестве универсального выступают числовые множества:
N, Z, Q, R.
Пересечение множеств
Начнем с задачи. В 3-м классе 35 учеников, из них 20 занимаются в спортивных секциях, 18 – в различных кружках, причем каждый ученик занимается хотя бы одним видом внеклассной работы: спортивным или кружковым. Сколько учеников занимаются одновременно спортом и в кружках?
А В
 А
А 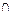 В
Рис. 2 В
Рис. 2
| Т.к. 20 + 18 = 38 и 38 > 35, то ясно, что круги А и В (здесь А и В соответственно множества учеников, занимающихся спортом и в кружках) должны налегать друг на друга, т.е. у них должна быть общая часть, которая не пуста. |
Решим задачу с помощью диаграммы Эйлера-Венна (рис. 2).
Путем рассуждений устанавливаем, что число учеников, которые занимаются спортом и в кружках, равно 3. Заметим так же, что
(20 + 18) – 35 = 3.
В этой задаче нам встретилось понятие общей части двух множеств. В теории множеств эта общая часть называется пересечением множеств.
Определение. Пересечением множеств А и В называют множество, состоящее из всех элементов, принадлежащих и множеству А и множеству В одновременно и обозначают А  В, т.е.
В, т.е.
А  В = { х | х Î А и х Î В }.
В = { х | х Î А и х Î В }.
Операция, при помощи которой находят пересечение множеств, называется также пересечением. На диаграмме Эйлера-Венна пересечение множеств А и В изображается заштрихованной областью (рис. 3).
 А В
А В
|
Рис. 3
Вообще, если множества А и В имеют элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются. В том случае, когда множества А и В не имеют общих элементов, то говорят, что их пересечение пусто и пишут: А  В = Æ. На диаграмме Эйлера-Венна такие множества изображаются при помощи двух кругов, не имеющих общих точек.
В = Æ. На диаграмме Эйлера-Венна такие множества изображаются при помощи двух кругов, не имеющих общих точек.
Понятие пересечения двух множеств можно обобщить на любое конечное число множеств.
П р и м е р ы.
1) А = { а, в, с }. В = { в, с, d }, А  В = { в, с }.
В = { в, с }.
2) А = { а, в, с }, В = { в, с, d }, С = { к, l, в }, А  В
В  С = { в }.
С = { в }.
3) Если А Í В Í С, то А  В
В  С = А.
С = А.
Рассмотрим свойства операции пересечения множеств.
Для любых множеств А, В, С:
1°. А  Æ = Æ;
Æ = Æ;
2°. А  А = А;
А = А;
3°. А  В = В
В = В  А – коммутативность пересечения;
А – коммутативность пересечения;
4°. А  (В
(В  С) = (А
С) = (А  В)
В)  С = А
С = А  В
В  С – ассоциативность пересечения;
С – ассоциативность пересечения;
5°. А  В <=> А
В <=> А  В = А;
В = А;
6°. А  U = А (U – универсальное множество).
U = А (U – универсальное множество).
Свойства 1°-4° вытекают из определения пересечения множеств.
Доказательство свойства 5°.
Если А  В, тогда все элементы множества А являются элементами множеств В, а это означает (по определению) А
В, тогда все элементы множества А являются элементами множеств В, а это означает (по определению) А  В = А.
В = А.
Докажем теперь А  В = А => А
В = А => А  В.
В.
Возьмем любой элемент а  А и проверим, что а
А и проверим, что а  В. Тем самым докажем А
В. Тем самым докажем А  В (по определению отношения
В (по определению отношения  ).
).
Итак, пусть а Î А, тогда в силу А  В = А получаем а Î А
В = А получаем а Î А  В, а это означает, по определению пересечения, что а Î В. Утверждение доказано.
В, а это означает, по определению пересечения, что а Î В. Утверждение доказано.
Доказательство свойства 6° следует из свойства 5° и определения универсального множества U.
Объединение множеств
Определение. Объединением множеств А и В называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В.
В определении есть слова «принадлежащие хотя бы одному». Математики договорились заменять это словосочетание более кратким «А или В». Заметим, что союз «или» употребляется в неразделительном смысле в отличие от обыденной жизни.
Объединение обозначается A  В, т.е.
В, т.е.
A  В = { х | х Î А или х Î В }.
В = { х | х Î А или х Î В }.
Операция, при помощи которой находят объединение множеств, называется также объединением.
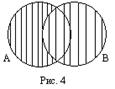
На диаграмме Эйлера-Венна объединение множеств A и В изображается заштрихованной областью (рис. 4).
|
|
П р и м е р ы.
1) А = {1, 2, 3}, В = {2, 3, 4}, А  В = {1, 2, 3, 4}.
В = {1, 2, 3, 4}.
2) А = {1, 2, 3}, В = { а, в, с, d }, А  B = {1, 2, 3, а, в, с, d }.
B = {1, 2, 3, а, в, с, d }.
3) А = {1, 2, 3}, В = {1, 2, 3, 4, 5}, А  В = В = {1, 2, 3, 4, 5}.
В = В = {1, 2, 3, 4, 5}.
4) A = {1, 2, 3}, В = {2, 3, 4}, С = { 3, 4, 5},
A  В
В  С = {1, 2, 3, 4, 5}.
С = {1, 2, 3, 4, 5}.
Рассмотрим свойства операции объединения множеств. Для любых множеств А, В, С:
1°. А  Æ = А;
Æ = А;
2°. А  А = А;
А = А;
3°. A  В = В
В = В  A – коммутативность объединения;
A – коммутативность объединения;
4°. А  (В
(В  С) = (А
С) = (А  В)
В)  С = А
С = А  В
В  С – ассоциативность объединения;
С – ассоциативность объединения;
5°. A Í В <=> A  В = В – закон поглощения;
В = В – закон поглощения;
6°. A  U = U.
U = U.
Свойства 1°-3° вытекают из определения объединения множеств.
Доказательство свойства 4°.
Пусть х Î А  (В
(В  С), т.е. х принадлежит хотя бы одному из множеств А или В
С), т.е. х принадлежит хотя бы одному из множеств А или В  С. Если х Î A, то х Î А
С. Если х Î A, то х Î А  В
В  С, если
С, если
х Î В  С, то х Î В или х Î С. В любом случае х Î А
С, то х Î В или х Î С. В любом случае х Î А  В
В  С.
С.
Аналогично доказывается обратное включение.
Доказательство свойства 5°.
A Í В => A  В = В очевидно. Пусть теперь А
В = В очевидно. Пусть теперь А  В = В, докажем А Í В.
В = В, докажем А Í В.
Пусть х Î А, тогда х Î A  В по определению объединения. Поскольку, А
В по определению объединения. Поскольку, А  В = В, то х Î В. Значит, А Í В по определению включения.
В = В, то х Î В. Значит, А Í В по определению включения.
Доказательство свойства 6° следует из свойства 5° и определения универсального множества U.
Все перечисленные выше свойства объединения можно проиллюстрировать на диаграмме Эйлера-Венна.
Замечание. Если над множествами производятся операции пересечения и объединения и в записи выражения отсутствуют скобки, то сначала выполняют операцию пересечения, а затем операцию объединения.







