Если изображению подлежит плос-кая кривая линия, то все её конструк-тивные элементы компланарны и поэ-тому на построение её ортогональных проекций распространяются все прави-ла построения проекций плоских фигур.
Вполне очевидно, что от особенностей
положения линии в пространстве зави-
сят изобразительные свойства её орто-
гональных проекций.
Как и любая плоская фигура, пло-ская кривая линия может занимать в пространстве общее положение и два вида частных, т.е., проецирующие и уровня.
Особенности, отличающие изобра-
зительные свойства проекций плоских кривых от проекций иных плоских фигур
определяются особенностями их струк-тур.
12.5.1. Изобразительные свойства ортогональных проекций окружности
1. Плоскость кривизны окружности в
положении плоскостей уровня
(рис.12.41)
1. а || П1 Þ а2 ^О1 О2, а1 = | a |;
2. b || П2 Þ b1 ^O1 O2, b2 = | b |;
3. c || П3 Þ с1 º О1 О2 º с2, с3 = | c |.
Общее ПРАВИЛО 1: Если плоскость
кривизны окружности занимает то
или иное положение плоскости уров-
ня, то проекция окружности на ту
плоскость проекций по отношению к
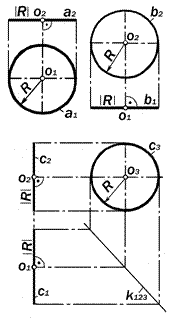
|
Рис. 12.41. Изобразительные свойства ортогональных проекций окружности в положениях плоскостей уровня

|
Рис. 12.42. Изобразительные свойства ортогональных проекций окружностей в проецирующих положений
которой она не параллельна, есть пря-мая линия, перпендикулярная к соот-ветствующей линии связи, а проекция на параллельную ей плоскость проек-ций - окружность, конгруэнтная дан-ной..
2. Плоскость кривизны окружности в проецирующих положениях
(рис. 12.42)
1. (aÉа) ^П1 Þ а1 º a1, а2 – эллипс;
А2В2 º А2 А1 = | AB |; C2D2 ^ A2 B2 ,
2. (bÉb) ^П2 Þ b2 º b2, b1 – эллипс;
А1 В1 º А2 А1 = | AB |; C1D1 ^ A1 B1 ,
3. (g Éc)^П3 Þ с3 º g3, с1, с2-эллипсы;
А2В2 º А3 А2 = А1В1 = |AB|; C2D2 º C1D1.
Общее ПРАВИЛО2: Если плоскость
кривизны окружности занимает то или иное проецирующее положение, то на перпендикулярные к ней плоскости
проекций она вырождается в наклон-
ные отрезки прямых, а на непарал-лельные к ней плоскости проекций, - в эллипсы, большие оси которых сов-падают с направлениями соответст-вующих линий связи и их длины равны величинам диаметров окружности, а малые оси перпендикулярны к большим в их серединах, и их длины равны про-изведению длин больших осей на ко-синус угла наклона плоскости кривиз-ны окружности к той плоскости про-
екций, на которую она проецируется в эллипс.
Графическим признаком того, что на рис.12.42. изображены окружности, а не эллипсы, является равенство длин их вырожденных проекций длинам боль-
больших осей их проекций – эллипсов.
3. Плоскость кривизны окружности
в общем положении
(рис.12.43)
Так как плоскость общего положе-ния не параллельна и не перпенди-кулярна ни к одной из плоскостей про-екций, то ни одна из проекций принад-лежащей ей окружности не является ни окружностью, ни прямой линией.
Отсюда следует вывод: Ортого-нальные проекции окружности, плоско-сть кривизны которой занимает в пространстве общее положение, явля-
ются эллипсами.
Пример 1. Построить комплексный чертёж окружности m радиуса R, при-надлежащей плоскости a(f ´ h) (рис. 12.43).
Анализ условия:
1. Плоскость кривизны окружности

|
Рис. 12. 43. Изобразительные свойства ортогональных проекций окружности в общем положении
общего положения задана линиями уровня, с которыми совпадают два её разных диаметра, параллельных П1 и П2 и поэтому их проекции на эти пло-скости являются большими осями иско-мых эллипсов.
2.Так как направления f и h не вза-
имно перпендикулярны, то проекции от-

|
Рис.12.44 Изобразительные свойства ортогональных проекций эллипсов в положениях плоскостей уровня
Рис. 12.45 Изобразительные свойства ортогональных проекций эллипса в проецирующих положениях
ложенных по ним диаметров не являют-
| ся сопряженными диаметрами, а поэ-тому для построения малых осей эл- липсов-проекций схема рис. 13.27 не-приемлема. 3. Решение задачи сводится к гра-фическому построению малых осей эллипсов горизонтальной и фронталь-ной проекций данной окружности. Решение: Построение малой оси эллипса го-ризонтальной проекции окружности. 1. 1, 2 Î h; 01 = 02 = R; 0111 = 01 21 = R; 12 , 22 Î h2 2. 3, 4 Î f; 03 = 04 = R; 0232 = 0242 = R; 31 , 41 Î f1. 3. 11, 21 Î h11 (R = 01 11 = 01 21); 4. 41 Î b1 ^ h1; 411 = b1 ´ a 11; 4101 = R; 411 01 = | R |; 5. 01 Î g1 || b1; 511 = g1 ´ m11; 6. 511 Î b11 || 411 01;51 = b1 . ´ g1; 7. 61 Î b1 || 01 41; 51 01 = 0181; 51 81 - искомая малая ось эл-липса горизонтальной проекции окружности. Построение малой оси эллипса фронтальной проекции окружности 1. 3242 Î f 12 (R = 0232 = 02 42); 2. 12 Î e2 ^ f2;112 = e 2 ´ m12; 3. 112 0 2 = | R |; 4. 12 Î q2 || 32 42; 92 = q 2 ´ 112 02 ; 5. 0292 – величина искомой малой полуоси; 6. 02 Î р2 ^ f2; 02102 = 02 112 – иско-. |

|
мая малая полуось эллипса фронталь-ной проекции окружности.
Имея значения и положение на ком-
плексном чертеже больших и малых осей эллипсов искомых ортогональных проекций окружности в плоскости об-щего положения, следует строить эти эллипсы по схеме рис.12.26.






