В архитектурном и дизайнерском проектировании наибольшее распро-странение имеют кривые линии второго порядка. Они носят название коничес-ких сечений, так как их можно получить в результате пересечения поверхности прямого кругового конуса плоскостями различного положения по отношению к её образующим (рис. 12.13).

|
Рис. 12.13. Виды конических сечений в зави-симости от положения секущей плоскости
Если плоскость пересекает все об-разующие и перпендикулярна к оси вра-
щения конуса, то её сечение называется
ется н о р м а л ь н ы м и является окружностью.

|
Рис. 12.14. Геометрическая модель
эллипса, её фокусов и директрис

|
Рис. 12.15. Геометрическая модель
параболы, её фокуса и директрисы
Если плоскость пересекает все об-
разующие поверхности, но не перпен-
дикулярна к оси её вращения, то в се-
чении будет замкнутая кривая – э л л и- п с (рис.12.14). При этом фокусы F1 и F2
эллипса конструктивно являются точка-
ми касания плоскости его кривизны поверхностями шаров, называемых ша-рами Данделена, вписанных в конус над и под этой плоскостью.
Что касается директрис d эллипса, то они являются рёбрами двугранных углов между секущей плоскостью a и параллельными плоскостями кривизны окружностей касания конической поверхности впи-санными в неё шарами Дан-делена.
Если плоскость a пересе-кает все образующие кониче-ской поверхности кроме одной, то в сечении будет разомкнутая кривая, содержащая одну не-собственную точку, -- п а р а –
б о л а (рис.12.15).
Фокусом F параболы является точка касания шара Данделена с плоскостью её кривизны, а директрисой –- линия пересечения этой плоскости с плоско-стью кривизны окружности а касания конической поверхности с вписанным в неё шаром.
Если плоскость a пере-секает все образующие кроме двух, то она пересекает обе полы конической поверхности, образуя двухветвевую разом-кнутую линию с двумя несоб-ственными точками, -- г и –
п е р б о л у (рис. 12.16).
Фокусами F1 и F2 гипер-болы конструктивно являются точки касания к плоскости a её кривизны двух конгруэнт-ных шаров Данделена, дирек-трисами d1, d2 – линии пере-сечения этой плоскости с дву-мя плоскостями кривизны окружностей а и b касания шаров Данделена с данной конической поверхностью.
Если провести секущую плоскость
через вершину S конуса параллельно
плоскости a, то она рассечет его повер-
хность по двум прямолинейным образу-
ющим, которые, будучи ортогонально спроецированными на плоскость a, оп-ределят а с и м п т о т ы полученной гиперболы.

|
Рис. 12 16. Геометрическая модель гиперболы с её фокусами, директрисами и асимптотами
Если вершину S принять за центр проецирования, то поверхность данного конуса станет проецирующей и линии, лежащие на ней, станут проецировать-ся или преобразовываться друг в дру-га.
Другими словами, эллипс, параболу и гиперболу можно получить путем цен-трального проецирования окружности на соответственно расположенные пло-скости, что делает эти линии проек-тивно эквивалентными.
При этом совершенно очевидно, что данная пространственная ситуация полностью удовлетворяет геометричес-
ким условиям теоремы Дезарга и поэто-
му эллипс, парабола и гипербола есть плоские кривые, перспективно-коллине-
арные окружностям касания соответст-
вующих шаров Данделена при цент-ре коллинеации в вершине конуса и осях коллинеации в виде соответствую-
щих директрис этих кривых.
Если вершину конуса удалить в бес-

|
Рис. 12.17. Геометрическая модель
эллипса, его фокусов и директрис на
цилиндрической поверхности

|
Рис.12.18. Прямой угол опирается
на диаметр окружности (дугу в 180°)

|
Рис.12.19. Угол в 45° опирается на
сторону вписанного квадрата (дугу в 90°)
конечность, то его двухпольная по-верхность преобразуется в однополь-ную цилиндрическую, проецирующую две конгруэнтные окружности касания шаров Данделена на наклонную секу-щую плоскость a в эллипс, фокусы F1, F2 и директрисы d1, d2 которого имеют такую же природу, как и у эллипса на поверхности конуса (рис.12.17).
Конструктивные свойства
кривых линий второго порядка
1. Окружность. (рис.12.18—12.21, см. также табл.1, п.1).
1. Любой диаметр АВ окружности а является гипотенузой однопараметри-ческого множества прямоугольных тре-угольников АВС, вершинами С которых являются точки этой окружности (рис. 12.18).
Получается, что линейный угол в 90° опирается на дугу окружности в 180° и их отношение равно 1: 2. Окружность замечательна тем, что это отношение сохраняется для любых действительных значений этих углов.
В частности, линейный угол в 45° опирается на сторону вписанного ква-драта (центральный угол - 90°), в 30°,-- на сторону вписанного правильного ше-стиугольника (т.е., на 60°) и т.д. (рис.
12.19).
Отсюда общее правило: Градусная мера линейного угла, вписанного в окружность, вдвое меньше градусной меры центрального угла той дуги окружности, на которую этот линей-ный угол опирается.
2. Медиана СО любого вписанного прямоугольного треугольника АВС раз-бивает его на два равновеликих треуго-льника, основания высот которых рас-полагаются на двух окружностях, диа-метрами которых являются половины гипотенузы АВ, т.е., радиусы данной окружности (рис.12.20). Площадь пря-моугольника О1С2 вдвое меньше пло-щади D АВС.
3.Длина окружности, диаметром ко-торой является радиус данной окружно-сти, равна длине половины данной ок-ружности.
4. Окружность – выпуклая гладкая кривая, обладающая центральной сим-
метрией её диаметрально противопо-ложных точек и осевой симметрией её точек относительно любого диаметра.
4. Продолжение катетов АС и ВD, AD и ВЕ двух любых исходных прямоу-гольных треугольников, вписанных в ок-ружность, до взаимного пересечения в точках 1, 2, 3, 4 образует четырёхуголь-

|
Рис. 12.20. Медиана ОС треугольника АВС
разбивает его на два равновеликих треугольника АОС и ВОС.
ники С1D2 и D3E4, диагонали 12 и 34 которых всегда перпендикулярны к диа-метру АВ окружности как к общей гипо-тенузе этих треугольников (рис. 12.21).

|
Рис.12. 21. Построение перпендикуляров, опущенных из точек вне окружности не её
диаметр.
В этом легко убедиться поняв, что эти диагонали являются третьими вы-сотами образованных таким построе-нием остроугольных треугольников А1В и А3В, две другие высоты которых яв-ляются катетами АЕ, АD, BC и BD, как бы заданными по условию.
2. Эллипс. (рис.12.22 – 12.27, см. также табл. 1, п.2).

|
Рис.12. 22. Конструктивные элемен-
ты эллипса

|
Рис.12. 23. Подэрное преобразование окружности в эллипс и построение его эволюты

|
Рис. 12.24. Сопряженные диаметры делят сопряженные с ними хорды пополам
1. Эллипс – замкнутая выпуклая
гладкая кривая линия, обладающая од-ним центром симметрии и двумя взаим-
но-перпендикулярными осями симме-
трии.
2. Нормаль n к эллипсу в произволь-ной точке Е является биссектрисой угла между её радиусами-векторами, прихо-дящими в эту точку.
3. Длины радиусов-векторов для каждой точки эллипса типа 1¢ соответ-ственно равны расстояниям от вершин А и В эллипса до произвольной точки 1 на фокальном отрезке F1 F2.
4. Касательная t к эллипсу в про- извольной точке Е перпендикулярна к соответствующей нормали и является биссектрисой угла, смежного с углом ме-жду радиусами-векторами точки Е.
Отсюда следует ПРАВИЛО:
Биссектрисы произвольных углов между двумя пересекающимися прямы-
ми всегда взаимно-перпендикулярны.
5. Система 4-х касательных в вер- шинах эллипса является описан-ным вокруг него габаритным пря-моугольником.
6. Система 4-х касательных к эллипсу в концах двух его сопря-женных диаметров является опи-санным вокруг него параллело-граммом (рис.12.24).
7.Сопряженные диаметры де-
делят сопряженные с ними хор-
ды пополам.
8. Если в один из фокусов эл-липса поместить источник света или звука, то их лучи, отражаясь от эл-липса, соберутся во втором фокусе. Это свойство эллипса используется в оптике и акустике.
9. Эллипс является линией, огиба-ющей совокупность последовательных положений одной стороны прямого ли-нейного угла, вершина которого пере-мещается по окружности, а вторая сто-рона проходит через точку F внутри круга, ограниченного этой окружностью
(рис. 12.23).
Определение 12.8. Геометричес-
кое место компланарных оснований перпендикуляров, опущенных из одной точки вне кривой линии на прямые, касательные к ней, называется п о –
д э р о й или подошвенной линией данной кривой относительно данной
точки [ 52].
В данном случае окружность является подэрой эллипса относительно его фо-куса F.
10. При заданном положении фоку-са F малая ось эллипса равна фокаль-ной хорде окружности-подэры, проходя-щей через фокус перпендикулярно бо-льшой оси АВ (рис. 12.25).

|
Рис.12.25. Построение малой оси эллипса и
директрисы по заданной большой полуоси и
одному фокусу.
11. При заданном фокусе F2 рассто-яние OL до соответственной ему дирек-трисы d2 равно длине гипотенузы ОЕ прямоугольного треугольника ОВЕ, по-добного треугольнику OF1N, один катет которого равен полуфокальному рассто-янию с, а второй – величине малой по-луоси ОС.
12. Основание L правой директрисы d2 является точкой пересечения касате-льных t1 и t2 к окружности радиуса, рав-ного большой полуоси эллипса, в кон-цах M и N её фокальной хорды.
Определение 12.9. Хорда окружно-сти, соединяющая точки касания к ней двух прямых, выходящих из одной точ-ки вне её, называется п о л я р о й этой точки относительно данной ок-ружности.
Определение 12.10. Точка, из ко-торой проведены две касательные к данной окружности, называется п о –л ю с о м её хорды, соединящей точки касания.
Так как все кривые второго порядка проективно-эквивалентны (потому, что могут взаимно преобразовываться друг
в друга), то отношение полюсов и поляр

|
Рис. 12.26. Построение точек эллипса
по его большой и малой осям

|
Рис.12.27. Определение осей
эллипса по его заданным элементам
относительно окружности сохраняется и
относительно эллипса, параболы и ги-перболы.
13.В силу взаимности отношения по-люсов и поляр относительно кривой
линии второго порядка основание дирек-
трисы эллипса является полюсом её фокальной хорды, которая, в свою оче-редь, является полярой основания ди-ректрисы.
14. Фокус эллипса является полю-сом его директрисы, которая, в свою очередь, является полярой его фокуса.
15. Эллипс, задаваемый большой и малой осями, является геометрическим местом вершин прямого угла прямоуго-льного треугольника, длина гипотенузы которого равна разности длин радиусов двух концентрических окружностей, по-строенных на этих осях, а катеты им со-ответственно параллельны (рис.12. 26). Это свойство преимущественно испо-льзуется в архитектурном черчении для построения точек эллипса по двум его осям.
Если эллипс задаётся другими его элементами (фокусами, вершинами, ди-ректрисами, сопряженными диаметрами в различных сочетаниях), то графичес-кие способы его построения сводятся к нахождению по этим элементам его бо-льшой и малой оси.
16. Эллипс может быть задан:
16.1.Большой АВ и малой СD осями
или их половинами (рис. 12.26).
16.2.Большой полуосью ОА и одним
фокусом F1 (рис.12.27, а).
16.3.Большой полуосью ОА и одной
директрисой d1 (рис. 12.27, б).
16.4.Одной директрисой d1 и одним
фокусом F1 (рис. 12.27, в).
16.5.Одной директрисой d1 и малой
полуосью ОС (рис.12.27, г).
16.6.Одним фокусом F1 и малой по-
луосью ОС (рис. 12.27, д).
16.7.Двумя сопряженными диамет-
рами 12 и 34 (рис.12.28).
17. Для графического построения большой АВ и малой СD осей эллипса по его заданным сопряженным диамет-рам 12 и 34 необходимо (рис.12.28):
1. полудиаметр О2 повернуть на 90°, переместив точку 2 в положение точки 5;
2. соединить точку 5 с точкой 3 и оп-
ределить середину 6 отрезка 35;
3.. радиусом О6 из точки 6 как из
центра провести окружность до пересе-чения с прямой, определяемой точками 3 и 5, в точках 7 и 8;
4. соединить точку О с точками 7 и 8, определив тем самым направления большой АВ и малой СD осей искомого эллипса;

|
Рис. 12. 28. Построение большой АВ и малой СD осей эллипса по его сопряженным диаметрам 12 и 34.
5. отложить по направлению О7 ве-личину малых полуосей ОС и ОD, рав-ную отрезку 57, а больших полуосей,- равную отрезку 58 диаметра 78 вспомо-гательной окружности с центром в точ-ке 6;
6. Построение остальных точек эл-липса производить по рис.12.26.
3. Гипербола (рис.12.29 - 12.31,
см. также табл.1, п.3).
1. Гипербола – выпуклая, гладкая, разомкнутая двухветвевая линия с од-ной действительной и одной мнимой осями симметрии, с двумя параллель-ными директрисами и с двумя пересе-кающимися прямолинейными асимпто-тами, с которыми её криволинейные ве-тви стремятся пересечься в бесконеч-ности (рис. 12.29).

|
Рис.12.29. Геометрическая модель гиперболы

|
Рис. 12.30. Гипербола как киноперс-пективная проекция точки
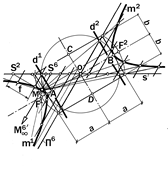
|
Рис. 12.31. Вид гиперболы при
остром угле между её асимптотами

|
Рис. 12.32. Подэрное преобразование
окружности в гиперболу относитель-
но её фокуса
2. Длины радиусов-векторов для ка-
ждой точки гиперболы типа М¢ равны расстояниям от её вершин до соот-ветствующих точек типа М, взятых на продолжении её действительной оси.
3. Представляя гипер-болу как траекторию движе-ния точки, рассмотрим слу-чай её образования в резу-льтате центрального подви-жного проецирования непо-движной точки А в неизме-няемой проекционной сис-теме S - П¢ [ 89].
Здесь s – траектория движения центра S, кото-рый занимает на ней ряд последовательных положе-
ний S1, S 2, S3, …S n.
Картина П¢ ^ s, удалён-
ная от центра S на посто-янное расстояние f, переме-щается параллельно самой себе, за-нимая фронтально-проецирующие поло-жения П1, П2, П3, … П n. Проецируя точку А из подвижного центра S на подвижную картину П¢, получаем ряд точек пересе-чения проецирующих лучей с соответ-ствующими положениями картины, ко-торые, будучи соединёнными непреры-вной линией, образуют равнобокую ги-перболу как киноперспективную про-екцию точки А.
Одной асимптотой этой гиперболы является траектория s движения цент-ра, а второй – вырожденная проекция того положения П4 картины П¢ ¢, которое соответствует положению S4 центра S, проецирующего точку А параллельным ей лучом.
Если угол между асимптотами сде-лать острым (рис.12.31), то принцип построения точек гиперболы не изме-нится.
При этом вершины А и В гиперболы определятся в пересечении биссек-трисы острого угла между асимптотами с построенными её ветвями. Рассто-яние АВ = 2а является большой и дей-ствительной осью гиперболы, малая и мнимая ось СD = 2b, равна расстоянию между точками пересечения касатель-ных t1 и t2 в вершинах А и В с асимпто-тами. Директрисы и фокусы гипербол на рис.12.30 и 12.31 строятся по схеме рис.12.29.
4. Касательная t к гиперболе в её
произвольной точке М является биссек-трисой угла между её радиусами-векто-
рами F1M и F2M.
5. Нормаль n к гиперболе перпен-дикулярна к касательной в точке М ка-сания и является биссектрисой угла, смежного с углом между радиусами-векторами (см. рис. 12.29).
6. Окружность, построенная на дей-ствительной оси АВ, является подэрой гиперболы относительно её фокуса F2 (или F1) (рис. 12.32).
7.При заданных фокусах F1, F2 и вершинах А и В положение директрис d1 и d2 определяется точками пересече-ния асимптот гиперболы с окружностью, построенной на действительной оси как на диаметре.

|
Рис. 12.33. Графическое построение
эволюты гиперболы
8. Эволютой одной ветви b гипербо-лы является кривая mb c точкой О в воз-врата первого рода в качестве центра кривизны гиперболы в вершине В как полюса вершинной хорды MN фока-льной окружности ОF1 F2 (рис.12.33).
9. Гипербола может быть задана:
9.1. Действительной полуосью ОА и фокусом F1 (рис.12.34, а);
9.2. Действительной полуосью ОА и директрисой d1 (рис. 12.34, б);
9.3. Действительной полуосью ОА и одной асимптотой k1 (рис. 12.34, в);
9.4. Фокусом F1, центром О и дирек-
трисой d1 (рис. 12.34, г);

|
Рис.12.34. Различные варианты задания гиперболы
9.5. Фокусом F1, центром О и одной
асимптотой k1 (рис. 12.34, д);
9.6. Директрисой d1, центром О и одной асимптотой k 1 (рис.12.34, е).
4. Парабола. (рис.12.35, 12.36, см. также табл. 1, п.4).
1. Парабола – это выпуклая, глад-кая одноветвевая разомкнутая кривая линия с одной действительной осью симметрии, одним фокусом, одной ди-ректрисой и одной несобственной точ-кой (рис.12. 35).
2. Касательная t к параболе в про-извольной точке М является биссек-трисой угла между фокальным радиу-сом FM и перпендикуляром, опущен-ным из точки М на директрису d.
3. Нормаль n к параболе в произ-вольной точке М перпендикулярна к ка-
сательной t и делит угол, смежный с углом между фокальным радиусом и

|
Рис. 12. 35. Геометрическая модель параболы
перпендикуляром к директрисе, попо-лам.
4.Величина параметра р параболы или расстояния от основания D дирек-трисы d до фокуса F вдвое меньше её
фокальной хорды ВС.
5. Основание D директрисы d явля-
ется полюсом фокальной хорды ВС, а
фокус F – полюсом директрисы d и на-
оборот, директриса d является полярой фокуса F, а фокальная хорда ВС – по-лярой основания D директрисы d.
6. Главная касательная t¢ является подэрой параболы относительно её фо-
куса F, что даёт возможность её графи-
ческого построения как огибающей вто-
рые стороны прямых линейных углов, вершины которых инцидентны этой ка-
сательной (рис.12.36).
7. Эволютой параболы а является кривая ma как огибающая последовате-
льные положения нормалей, перпенди-
кулярных к касательным в точках их ка-сания к параболе.
Графически точки касания парабо-
лы ко вторым звеньям производящей ломаной являются основаниями высот треугольников, образованных по счету
четными и нечетными положениями этих звеньев. Высоты этих треугольни-
ков определяют третьи звенья – норма-.

|
Рис.12.36 Подэрное преобразование прямой линии в параболу относительно её фокуса и построение её эволюты
ли к параболе, которые огибают её эво-люту.
По построению получается, что центр ОА кривизны параболы в вер-шине А удалён от фокуса F так же, как
фокус F удалён от вершины А, а верши-
на А, -- от директрисы d.






