Математическое ожидание дохода по i-й ценной бумаге (mi) рассчитывается следующим образом:
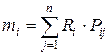 , (7)
, (7)
где Ri – возможный доход по i-й ценной бумаге, руб.;
Pij – вероятность получение дохода;
n – количество ценных бумаг.
Для измерения риска служат показатели рассеивания, поэтому чем больше разброс величин возможных доходов, тем больше опасность, что ожидаемый доход не будет получен. Мерой рассеивания является среднеквадратическое отклонение:
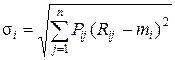 . (8)
. (8)
В отличии от вероятностной модели, параметрическая модель допускает эффективную статистическую оценку. Параметры этой модели можно оценить исходя из имеющихся статистических данных за прошлые периоды. Эти статистические данные представляют собой ряды доходностей за последовательные периоды в прошлом.
Любой портфель ценных бумаг характеризуется двумя величинами: ожидаемой доходностью
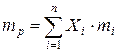 , (9)
, (9)
где Xi – доля общего вложения, приходящаяся на i-ю ценную бумагу;
mi – ожидаемая доходность i-й ценной бумаги, %;
mp – ожидаемая доходность портфеля, %
и мерой риска – среднеквадратическим отклонением доходности от ожидаемого значения
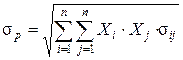 (10)
(10)
где sp – мера риска портфеля;
sij – ковариация между доходностями i-й и j-й ценных бумаг;
Xi и Xj – доли общего вложения, приходящиеся на i-ю и j-ю ценные бумаги;
n – число ценных бумаг портфеля.
Ковариация доходностей ценных бумаг (sij) равна корреляции между ними, умноженной на произведение их стандартных отклонений:
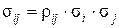 (11)
(11)
где rij – коэффициент корреляции доходностей i-ой и j-ой ценными бумагами;
si, sj – стандартные отклонения доходностей i-ой и j-ой ценных бумаг.
Для i = j ковариация равна дисперсии акции.
 |
Рассматривая теоретически предельный случай, при котором в портфель можно включать бесконечное количество ценных бумаг, дисперсия (мера риска портфеля) асимптотически будет приближаться к среднему значению ковариации.
Графическое представление этого факта представлено на рисунке 2.1.
Рисунок 2.1 – Риск портфеля и диверсификация
Совокупный риск портфеля можно разложить на две составные части: рыночный риск, который нельзя исключить и которому подвержены все ценные бумаги практически в равной степени, и собственный риск, который можно избежать при помощи диверсификации. При этом сумма вложенных средств по всем объектам должна быть равна общему объему инвестиционных вложений, т.е. сумма относительных долей в общем объеме должна равняться единице.






