Б.П. Зеленцов
АЛГЕБРА и геометрия
Практикум
Рекомендовано УМО по образованию в области телекоммуникаций в качестве практикума для студентов высших учебных заведений, обучающихся по направлению 210400 «Телекоммуникации»
Новосибирск
УДК 51(076)
Б.П. Зеленцов. Алгебра и геометрия: Практикум / ГОУ ВПО «СибГУТИ». - Новосибирск, 2010. – 88 с.
Практикум содержит планы 17 практических занятий, сводки формул, словарь основных терминов по теме пособия и список литературы. Практикум охватывает следующие основные темы: линейная алгебра, векторная алгебра, линейные образы аналитической геометрии, кривые и поверхности второго порядка. Практикум предназначен для использования в учебном процессе преподавателями и студентами дневной формы обучения при изучении математики на первом курсе по направлению подготовки дипломированных специалистов 210400 «Телекоммуникации».
Кафедра высшей математики
Табл. – 34, список литературы – 24 назв.
Рецензенты: д.ф.-м.н., профессор Г.Г. Черных
д.т.н., профессор В.Н. Максименко
к.ф.-м.н., доцент Ю.Г. Боковиков
Утверждено редакционно-издательским советом ГОУ ВПО «СибГУТИ» в качестве практикума
© Б.П. Зеленцов, 2010 г.
© ГОУ ВПО «Сибирский государственный университет телекоммуникаций и информатики», 2010 г.
ОГЛАВЛЕНИЕ
| ПРЕДИСЛОВИЕ ……………………………………………..…………… |
| ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ………………………………………….. Занятие 1. Матрицы...................………………………………..………. Занятие 2. Определители...............…………………………………… Занятие 3. Обратная матрица. Ранг матрицы............................ Занятие 4. Формулы Крамера. Матричные уравнения ……. Занятие 5. Метод Гаусса...........................………………………...….. Занятие 6. Исследование системы линейных уравнений..................................................... Занятие 7. Геометрический вектор...........................……….....…. Занятие 8. Вектор в декартовых координатах..............…...... Занятие 9. Скалярное произведение ДВУХ ВЕКТОРОВ.....…. Занятие 10. Векторное и смешанное произведения ……. | |
| Занятие 11. Прямая линия на плоскости....................……. Занятие 12. Прямая линия на плоскости................................ Занятие 13. Плоскость в пространстве.......……....................... Занятие 14. Прямая и плоскость в пространстве.……........ Занятие 15. Кривые второго порядка..........................……........ Занятие 16. Упрощение уравнений кривых второго порядка ……………………………………... Занятие 17. Поверхности второго порядка………………… |
| СВОДКИ ФОРМУЛ...........................................................……………… Раздел 1. матрицы, Определители, системы линейных уравнений…………………….. Таблица 1.1. Используемые обозначения ……………………………… Таблица 1.2. Виды числовых матриц …………………………………… Таблица 1.3. Некоторые операции с матрицами ……………………..… Таблица 1.4. Свойства линейных операций над матрицами ……..…… Таблица 1.5. Вычисление определителей ……………………………..…. Таблица 1.6. Свойства определителей …………………………………… Таблица 1.7. Обратная матрица ………………………………………...… Таблица 1.8. Свойства вырожденной квадратной матрицы А…….…… Таблица 1.9. Свойства ранга матрицы ……………………………….…… Таблица 1.10. Системы линейных уравнений ……………………………. Таблица 1.11. Матричные уравнения ……………………………….…… Таблица 1.12. Схема исследования системы линейных уравнений ……. |
| Раздел 2. Векторная алгебра ………………………………………. Таблица 2.1. Используемые обозначения ……………………………… Таблица 2.2. Геометрический вектор …………………………………… Таблица 2.3. Скалярное произведение ….……………………….……… Таблица 2.4. Векторное произведение ………………………..….……… Таблица 2.5. Смешанное произведение ………………….………..……… |
| Раздел 3. линейные образы Аналитической геометрии …. | ||
| Таблица 3.1. Используемые обозначения ……....…...………….................. Таблица 3.2. Уравнения прямой на плоскости....…...…………................. Таблица 3.3. Частные случаи положения прямой на плоскости ………. Таблица 3.4. Взаимное расположение двух прямых на плоскости.......... Таблица 3.5. Уравнения плоскости в пространстве........……….………..... Таблица 3.6. Частные случаи положения плоскости в пространстве …… Таблица 3.7. Взаимное расположение двух плоскостей......……………… Таблица 3.8. Уравнения прямой в пространстве.................……….……... Таблица 3.9. Взаимное расположение двух прямых в пространстве......... Таблица 3.10. Взаимное расположение прямой и плоскости......………. Таблица 3.11. Расстояние от точки до прямой на плоскости и до плоскости в пространстве ………………………….. |
| Раздел 4. Кривые И ПОВЕРХНОСТИ второго порядка ………… | |
| Таблица 4.1. Канонические уравнения кривых второго порядка................ Таблица 4.2. Свойства кривых второго порядка…………………............... Таблица 4.3. Преобразование декартовой прямоугольной системы координат на плоскости ……………………………. Таблица 4.4 Нахождение матрицы поворота к главным направлениям квадратичной формы ……………………….. Таблица 4.5. Схема упрощения уравнения кривой второго порядка …… Таблица 4.6. Канонические уравнения поверхностей второго порядка...... |
| СЛОВАРЬ ОСНОВНЫХ ТЕРМИНОВ ……………………………….. Раздел 1. матрицы, Определители, системы линейных уравнений …………………… Раздел 2. Векторная алгебра ……………………………………… | ||
Раздел 3. линейные образы Аналитической геометрии ….
Раздел 4. Кривые второго порядка ……………………………….
Раздел 5. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА…............…………..
|
ПРЕДИСЛОВИЕ
Пособие содержит учебный материал для подготовки и проведения практических занятий и выполнения домашних.
Каждый преподаватель использует материал данного пособия в соответствии с государственным образовательным стандартом и рабочей программой дисциплины по реализации этого стандарта. При необходимости преподаватель может изменить количество задач для аудиторного и домашнего задания в зависимости от контингента студентов и реального распределения часов. Преподаватель может также перенумеровать занятия.
Материал настоящего пособия логически разбит на четыре раздела:
| Наименование раздела | Номера занятий |
| 1. Матрицы, определители, системы линейных уравнений 2. Векторная алгебра 3. Линейные образы аналитической геометрии 4. Кривые и поверхности второго порядка | 1 - 6 7 - 10 11 - 14 15 - 17 |
В соответствии с этим разбиением приведены сводки формул и словарь основных терминов.
К каждому практическому занятию приводится изучаемый материал, теорию которого студент должен подготовить в качестве домашнего задания по конспекту лекций или по учебникам. Затем, в виде таблицы приведены номера задач, подлежащих решению. Как правило, задачи разбиты по типам в соответствии с изучаемым материалом. Номера задач к каждому практическому занятию приведены в трех столбцах: левый столбец содержит номера задач, решаемых в аудитории, средний - задаваемых на дом, а правый столбец содержит номера задач дополнительного задания.
Основным источником задач являются сборники [6, 12,17]; несколько задач взяты из методических указаний по линейной и векторной алгебре (Новосибирск, НЭИС, 1976, составитель И.Д.Суздальницкий).
Целью каждого практического занятия является усвоение студентами новых математических терминов и понятий, овладение новым теоретическим материалом, приобретение умения и навыков решения типовых математических задач в соответствии с принятой программой. Для достижения этой цели преподаватель должен научить студентов: определять тип математических объектов; сознательно применять основные теоремы и теоретические положения для решения задач; методам и алгоритмам решения типовых задач; методам выполнения изучаемых математических операций.
Пособие содержит справочный материал - сводки формул и словарь основных терминов. Этот справочный материал может быть использован не только при изучении математики, но и на старших курсах при изучении специальных дисциплин, а также при подготовке и защите курсовых и дипломных проектов. Следует отметить, что в словаре основных терминов предпочтение отдается определениям в словесной форме. В некоторых случаях приведены формально различные определения, взятые из разных источников. Совместно с определениями даются обозначения, используемые в настоящем пособии.
Автор будет признателен преподавателям и студентам, которые выскажут критические замечания и дадут полезные советы по всем аспектам этого учебного издания.
-------------------------------------------------------------------------------------------------------------- ПосАиГ-П-2-07
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 1. матрицЫ
Изучаемый материал: понятие числовой матрицы; виды матриц; линейные операции над матрицами; умножение матриц; понятие матричного многочлена; транспонирование матриц.
| Типы задач | Аудиторное задание | Домашнее задание | Дополнительное задание | ||||||||||
| 1. Линейные операции над матрицами | 1.1 | 1.9 | 1.18, 1.19 | ||||||||||
| 2. Произведение матриц | 1.2 - 1.4 | 1.10 - 1.14 | 1.20-1.29 | ||||||||||
| 3. Многочлен от матрицы | 1.5 - 1.7 | 1.15, 1.16 | 1.30-1.32 | ||||||||||
| 4. Транспонирование | 1.8 | 1.17 | 1.33-1.35 | ||||||||||
1.1.Найти линейные комбинации матриц: а) A + 2 B, б) A - B, в) 2 A + 4 B,
где A = 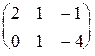 ; B = ; B = 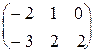 .
1.2. Вычислить AB, BA, AB - BA, если A = .
1.2. Вычислить AB, BA, AB - BA, если A =  , B = , B = 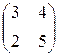 . .
| |||||||||||||
| 1.5. Найти значение матричного многочлена f (A) от матрицы A: f (x) = 3 x 2 - 4, где | A = 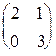 . .
| ||||||||||||
| 1.6. Показать, что матрица A является корнем многочлена P (x) = x 2 - 4 x +5. | A = 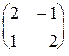
| ||||||||||||
| 1.7. При каких значениях a и b матрица A является корнем многочлена P (x) = x 2 +a x +b. | A = 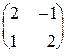
| ||||||||||||
| 1.8. Выполнить транспонирование матриц: | а) A = 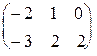 , б) B = , б) B =  . .
| ||||||||||||
Домашнее задание 1
1.9.Найти линейные комбинации матриц: а) 3 A + 2 B, б) 3 A - 2 B,
где A = 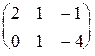 ; B = ; B = 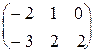 . .
|
1.10. Вычислить AB, BA, AB - BA, если A =  , B =
, B =  .
.
| Вычислить произведение матриц: | 1.11. 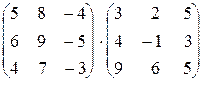 . .
| |||
1.12.  . .
| 1.13. 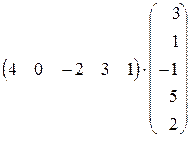 . .
|
1.14. 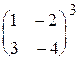 . .
| ||
| 1.15. Найти значение многочлена f (A) от матрицы A: f (x) = x 2 - 3 x + 1, где | A =  . .
| ||||
| 1.16. Найти значение матричного многочлена f (A), если f (x) = 2 x 3- 3 x 2 + 5, где | A =  . .
| ||||
| 1.17. Проверить свойство (AB)T = B T A T на примере: | A =  , B = , B =  . .
| ||||





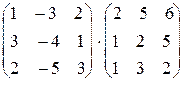 . 1.4.
. 1.4. 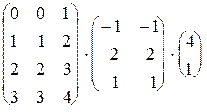 .
.

