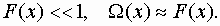
Ведущая функция параметра потока отказов стареющих элементов для любого момента времени или для пробега удовлетворяет следующему неравенству:
(8.36)
Для любого закона распределения наработка на отказ, имеющая конечную дисперсию D = 
, ведущая функция параметра потока отказов при достаточно большом значении x определяется по следующей формуле:
(8.37)
При расчете гарантированных запасов необходима интервальная оценка ведущей функции параметра потока отказов (для достаточно больших значений x)
(8.38)
где z 
– нормированное отклонение для нормального закона распределения при условии, что число отказов (замен) с вероятностью 1 – будет заключено в данных пределах.
Таким образом, используя значения параметра потока отказов, можно определить конкретный расход деталей за любой заданный период и планировать работу системы снабжения.
Параметр потока отказов может быть оценен на основании экспериментальных данных (отчетных материалов, специальных наблюдений) следующим образом (см. рис. 8.6):
(8.39)
где m (x) – суммарное число отказов n автомобилей в интервале пробега от x 1 до x 2 (или времени работы от t 1 до t 2); 
(x 1) и (x 2) – ведущие функции потока отказов к пробегу x 1 и x 2.
В общем случае параметр потока отказов непостоянен во времени, т. е. 
. Наблюдаются три основных случая поведения параметра по наработке (времени).
Первый случай (рис. 8.7, линия 1) – полное восстановление ресурса после каждого отказа, т. е.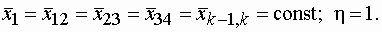 
При этом происходит стабилизация параметра потока отказов на уровне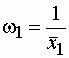 
.
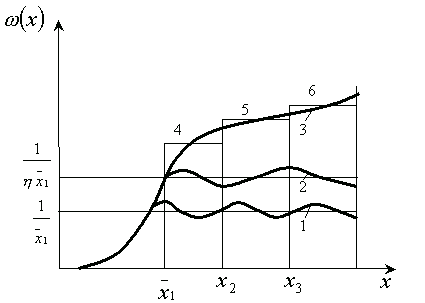
Рис.8.7 Случай изменения параметра потока отказа по наработке с начала эксплуатации
Второй случай (рис.8.7, линия 2) – неполное, но постоянное восстановление ресурса после первого отказа, т. е. 1 > 
= const. Для этого случая также характерна стабилизация параметра потока отказов, но на более высоком уровне:
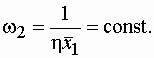
Третий случай (рис.8.7, линия 3) – последовательное снижение полноты восстановления ресурса, т. е.
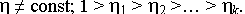
В этом случае и параметр потока отказов непрерывно увеличивается, что приводит к постоянному повышению нагрузки на ремонтные подразделения предприятия. Однако при расчетах для этого случая можно принимать 
= const как среднюю для отдельных периодов 4, 5 и 6, на которые разбивается весь пробег или время работы автомобиля. Подобный подход возможен также при анализе изменения параметра потока отказов в течение года (рис. 8.8). Этот параметр может приниматься практически постоянным для зимнего ( з), осенне-весеннего ( о, в) и летнего ( л) периодов.
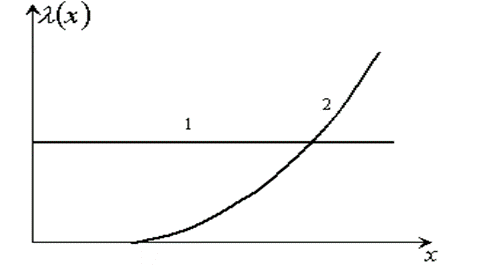
Рис.8.8. Случай изменения параметра потока отказа по временам года (сезонное)
Изучение закономерностей изменения параметров технического состояния автомобиля, его КЭ под влиянием различных факторов в процессе его эксплуатации необходимо для решения основных задач ТЭА. Знание этих закономерностей имеет существенное значение для разработки и эффективного применения научно обоснованных методов и нормативов поддержания автомобилей в технически исправном состоянии, т.е. управления их работоспособностью. Эти методы базируются на использовании математической статистики, теории вероятностей, теории надежности, диагностики и других дисциплин, при умелом применении компьютерной техники.
