Экспоненциальный закон распределения

Предположим, что в начальный момент x ₀ = 0 элементы численностью N ₀ были исправны. При работе происходят отказы этих элементов таким образом, что независимо от проработанного времени x число отказов ( N) в небольшом интервале времени x пропорционально числу оставшихся исправных элементов N_x, а непосредственно перед отказом элемент находится в исправном состоянии,

т. е. где — положительная постоянная, а знак минус свидетельствует о сокращении N_x при работе.

При x -> 0 имеем

После интегрирования ln N_x = – x – ln C,

откуда N_x = C exp[– x ]. (8.23)

При x ₀ = 0, C = N ₀, откуда N = N ₀ exp [– x ].

Но , тогда вероятность безотказной работы

(8.24)

Данное уравнение характеризует вероятность безотказной работы при экспоненциальном законе распределения ресурса до отказа, а – параметр потока отказов (называемый также для экспоненциального распределения интенсивностью отказов), равный обратной величине средней наработки на отказ, т.е. 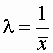. Плотность распределения для экспоненциального закона описывается уравнением

(8.25)

При этом законе распределения коэффициент вариации v = 1.

Экспоненциальный закон распределения является однопараметрическим (), что облегчает расчеты и объясняет широкое его применение на практике. В соответствии с теоремой умножения вероятностей вероятность безотказной работы к моменту x + x равна вероятности безотказной работы в течение времени x, умноженной на вероятность безотказной работы за время x, т. е. R (x + x) = R (x) R ( x) = exp[– (x + x)], отсюда

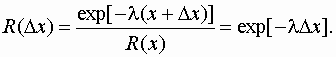(8.26)

Следовательно, при экспоненциальном законе распределения вероятность безотказной работы не зависит от того, сколько проработало изделие с начала эксплуатации, а определяется конкретной продолжительностью рассматриваемого периода или пробега x, называемого временем выполнения задания. Таким образом, рассмотренная модель не учитывает постепенного изменения параметров технического состояния, например, в результате изнашивания, старения и так далее, а рассматривает так называемые нестареющие элементы и их отказы. Экспоненциальный закон используется чаше всего при описании внезапных отказов, продолжительности разнообразных ремонтных воздействий и в ряде других случаев.

Кроме перечисленных, встречаются и другие законы распределения: гамма-распределения, Релея, Пуассона и прочие, сведения о которых можно получить из специальной литературы. Важно при этом подчеркнуть, что понимание процессов изменения технического состояния, знание соответствующих законов распределения случайных величин серьезно облегчает и делает более точными инженерные расчеты, а также позволяет предвидеть вероятность наступления тех или иных событий. Например, если известно, что закон распределения нормальный, расчеты надежностных характеристик сводятся к использованию нормированной функции. Для экспоненциального и закона распределения Вейбулла – Гнеденко также построены таблицы или простые линейные номограммы – “вероятностная бумага”.

Важным показателем надежности является интенсивность отказов (x) – условная плотность вероятности возникновения отказа невосстанавливаемого изделия, определяемая для данного момента времени при условии, что отказа до этого момента не было. Аналитически для получения (x) необходимо элементарную вероятность отнести к числу элементов, не отказавших к моменту x, т. е. .

Так как вероятность безотказной работы то . Учитывая, что , получаем

(8.27)