Проверка статистических гипотез. Проверка гипотез о законе распределения

 

Информация, полученная по выборке, может быть использована для оценки правомерности некоторых предположений (гипотез) о генеральной совокупности.

Статистической гипотезой называют любое утверждение о виде или свойствах распределения наблюдаемых в эксперименте случайных величин.

Гипотезы о неизвестном параметре Θ распределения бывают простые (Θ = Θ₀) и сложные (Θ < Θ₀, Θ > Θ₀, Θ ≠ Θ₀).

Проверяемую гипотезу обозначают H ₀, альтернативную – H ₁. Гипотезу проверяют на основании выборки. Случайный характер выборки может приводить к ошибкам. Ошибка первого рода имеет место тогда, когда отвергается верная гипотеза H ₀. Вероятность такой ошибки называется уровнем значимости и обозначается α. Чем меньше α, тем меньше вероятность отклонить верную гипотезу.

При ошибке второго рода отвергается верная на самом деле альтернативная гипотеза – H ₁ (принимается неверная гипотеза H ₀). Вероятность этой ошибки обозначают через β, а (1–β) называется мощностью критерия. Обычно при заданном уровне значимости α отыскивается критерий с наибольшей мощностью.

Проверка статистической гипотезы состоит из следующих этапов:

- определение гипотез H ₀ и H ₁;

- выбор статистики критерия (испытывать гипотезу можно на основе любой статистики, имеющей любое вероятностное распределение) и задание уровня значимости α;

- по статистике критерия и уровню значимости α определяют границу (квантиль), определяющую критическую область (т.е. область отклонения гипотезы H ₀);

- по выборке подсчитывают значение критерия;

- если фактически наблюдаемое значение критерия попадает в критическую область, то основная гипотеза H ₀ отклоняется и принимается H ₁.

Проверка гипотез о законе распределения

Рассмотрим, как можно проверить гипотезу о распределении генеральной совокупности.

Пусть (x ₁, x ₂, … x_m) – выборка из генеральной совокупности ξ с неизвестной функцией распределения, о которой выдвинута простая гипотеза H ₀: F _ξ(x)= F (x), где F (x) полностью задана. Это распределение назовем теоретическим. Альтернативное распределение в данном случае не конкретизируется и речь идет просто о согласии данных и гипотезы H ₀.

Для проверки таких гипотез разработано несколько критериев согласия, раиболее известным является критерий Пирсона (χ²: хи-квадрат). При использовании χ² –критерия вся область изменения генеральной совокупности делится на m интервалов (которые могут иметь различную длину). По выборке по этим же интервалам составляется статистический ряд (x_i → n_i, где n – объем выборки: ) и вычисляются оценки параметров теоретического распределения. Тем самым теоретическое распределение будет полностью определено. Теперь по теоретическому распределению подсчитывают вероятности p_i того, что случайная величина X принимает значения из i -го интервала по формуле

P (α≤X≤β) = F (β)– F (α).

По найденным p_i ищутся теоретические частоты (m_i = n · p_i).

Гипотеза H ₀ верна, если теоретические (m_i) и эмпирические (n_i) частоты достаточно мало отличаются друг от друга. В 1900 году К. Пирсон предложил использовать в качестве меры отклонения эмирических данных (n_i) от гипотетических значений (m_i) следующую статистику

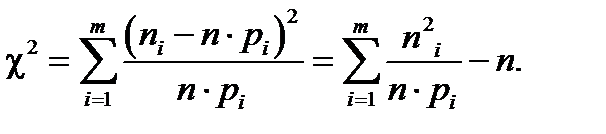
Согласно теореме Пирсона эта величина при имеет χ² – распределение с числом степеней свободы (k = m – r –1), m – число интервалов выборки, r – число параметров гипотетического распределения. Чем больше χ², тем хуже согласованы теоретическое и эмпирическое распределения.

Поскольку относительная частота события является состоятельной оценкой его вероятности, то при больших n разности в сумме должны быть малы и, следовательно, значение статистики не должно быть слишком большим. При достаточно большом значении χ² нужно отвергнуть гипотезу H ₀. Поэтому естественно задать только правостороннюю критическую область для гипотезы H ₀ в виде , где критическая граница t _α при заданном уровне значимости α должна быть выбрана из условия

Пример 32. Пользуясь критерием согласия Пирсона, проверить при уровне значимости α=0,01 гипотезу H ₀ о том, что случайная величина X, статистический ряд которой приведен в таблице, распределена по нормальному закону.

Интервалы значений xi	(-4, -3)	(-3, -2)	(-2, -1)	(-1, 0)
Относительные частоты pi *	0,012	0,050	0,144	0,266
Интервалы значений xi	(0, 1)	(1, 2)	(2, 3)	(3, 4)
Относительные частоты pi *	0,240	0,176	0,092	0,020

 

Решение. Для вычисления вероятностей p_i необходимо вычислить параметры, определяющие нормальный закон распределения (a и σ). Их оценки, рассчитанные по выборке объемом n = 500, дадут значения 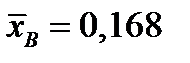и .

Используя формулу

,

находим для каждого i -го интервала вероятность p_i (вероятность попадания в i -й интервал случайной величины X, подчиненной нормальному закону распределения с параметрами , ) и результат оформим таблицей.

 

Интервалы значений xi	(-4, -3)	(-3, -2)	(-2, -1)	(-1, 0)
Вероятности pi	0,0126	0,0522	0,1422	0,2433
Интервалы значений xi	(0, 1)	(1, 2)	(2, 3)	(3, 4)
Вероятности pi	0,2668	0,1789	0,0770	0,0212

 

По данным двух таблиц вычислим наблюдаемое значение статистики Пирсона χ² . Получим χ² = 3,99.

Теперь определяем число степеней свободы k; так как количество интервалов равно m =8, а число параметров нормального распределения r =2, то k =8–2–1=5. По таблице распределения Пирсона для k =5 и α=0,01 найдем 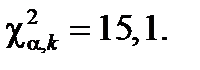Так как , то нет оснований отвергать проверяемую гипотезу.

 

4 ПРИНЦИПЫ ПОСТРОЕНИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

 

Основная цель и задача современной математики, по-видимому, состоит в реализации универсального математического метода познания. Это предполагает в первую очередь построение новых математических моделей в биологии, мироздании, микромире, в экономических и социальных явлениях.

В сравнении с натуральным экспериментом математическое моделирование имеет следующие преимущества:

- экономичность;

- возможность моделирования гипотетических, то есть не реализованных в натуре объектов;

- возможность реализации режимов, опасных или трудновоспроизводимых (критический режим ядерных реакторов и др.);

- возможность изменения масштабов времени;

- легкость многоаспектного анализа;

- большая прогностическая сила.

Постановка задачи (по Минскому): объект А является моделью объекта В, если наблюдатель с помощью А получает интересующие его сведения относительно В.

Модель концентрирует в себе записанную на определенном языке (естественном, алгоритмическом, математическом) совокупность наших знаний, представлений и гипотез о соответствующем объекте или явлении.

Модель лишь приближенно описывает поведение реальной системы, так как знания не бывают абсолютными, а гипотезы вынужденно или намеренно не учитывают некоторые эффекты.

С. Балтеру принадлежит высказывание: «Хотя аналогия часто вводит в заблуждение, это наименьшее из того, что вводит нас в заблуждение».

Это мысль подтверждается важнейшей особенностью модели, которая состоит в том, что знания об объекте можно неограниченно накапливать и при этом не терять целостного взгляда на него.

При исследовании сложных систем может потребоваться набор моделей, соответствующих различным уровням рассмотрения.

«Полная» модель будет полностью соответствовать оригиналу в смысле, что «наилучшей моделью кота является тот же самый кот».

Адекватность модели устанавливается проверкой для нее основных законов и сопоставлением результатов моделирования частных вариантов с известными для этих вариантов решениями (тестирование).

Модель всегда содержит параметры. Задачей идентификации является определение значений рабочих параметров модели. Они определяются в результате наблюдения над реальной системой. Решается задача по минимизации функционала отклонения траектории модели от траектории исследуемой системы. Традиционно применяются метод наименьших квадратов и наибольшего правдоподобия. Выявление значимых параметров и пренебрежение остальными позволяет уменьшить их число. Для этого считают коэффициенты чувствительности (регрессии) выходных показателей по отношению к входным.

При классификации методов моделирования и моделей различают аналитические, имитационные и комбинированные модели.

В аналитическом моделировании функционирование системы записывают в виде алгебраических, интегральных, дифференциальных и других соотношениях и логических условий.

Аналитическая модель может быть исследована следующими методами:

а) качественным, когда устанавливаются лишь некоторые свойства решения;

б) аналитическим, когда стремятся получить явные зависимости для искомых характеристик;

в) численным, когда получают числовые значения для заданных входных данных.

Математическая модель может использоваться традиционным способом, т.е. для получения какого-то частного решения, но и в сфере управления она успешно применяется для имитационного моделирования.

При имитационном моделировании алгоритм, реализующий модель, воспроизводит процесс функционирования системы во времени и в пространстве. Имитационное моделирование применимо к задачам, не поддающимся аналитическим и численным методам. Его иногда называют статистическим, поскольку заключительная обработка результатов выполняется методами математической статистики.

Имитационное моделирование позволяет оценить различные стратегии, обеспечивающие достижение цели данной системы.

Итак, модель нужна для того, чтобы:

- понять, как устроен конкретный объект (его структура, свойства, законы развития);

- определять наилучшие способы управления объектом или процессом при заданных целях и критериях;

- прогнозировать последствия воздействия на объект.