Во многих случаях мы располагаем информацией о виде закона распределения случайной величины (нормальный, бернуллиевский, равномерный и т. п.), но не знаем параметров этого распределения, таких как M[x], D[x]. Для определения этих параметров применяется выборочный метод.
Пусть выборка объема n представлена в виде вариационного ряда. Назовем выборочной средней величину
Величина 
называется относительной частотой значения признака xi.
Если значения признака, полученные из выборки, не группировать и не представлять в виде вариационного ряда, то для вычисления выборочной средней нужно пользоваться формулой
.
Естественно считать величину 
выборочной оценкой параметра M x.
Выборочная оценка параметра, представляющая собой число, называется точечной оценкой.
Выборочную дисперсию 
можно считать точечной оценкой дисперсии D [x] генеральной совокупности.
Используя выборочный метод можно сделать некоторые выводы о наличии или глубине корреляционной связи случайных величин x иh, даже не зная закона совместного их распределения. Выборку объема n в этом случае представим в виде таблицы, где i -й отобранный объект (i = 1, 2,..., n)представлен парой чисел xi, yi:
| x 1 | x 2 | ... | xn | |
| y 1 | y 2 | ... | yn | |
Выборочный коэффициент корреляции рассчитывается по формуле
Здесь
, 
Выборочный коэффициент корреляции можно рассматривать как точечную оценку коэффициента корреляции rxh, характеризующего генеральную совокупность.
Выборочные параметры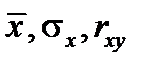 
или любые другие зависят от того, какие объекты генеральной совокупности попали в выборку и различаются от выборки к выборке. Поэтому они сами являются случайными величинами.
Пусть выборочный параметр dрассматривается как выборочная оценка параметра D генеральной совокупности и при этом выполняется равенство
M [d] = D ..
Такая выборочная оценка называется несмещенной.
Для доказательства несмещённости некоторых точечных оценок будем рассматривать выборку объема n как систему n независимых случайных величин x1,x2,... x n, каждая из которых имеет тот же закон распределения с теми же параметрами, что и случайная величина x, представляющая генеральную совокупность. При таком подходе становятся очевидными равенства:
M [ xi ] = M [x i ] = M [x]; D [ xi ] = D [x i ] = D [x]
для всех i = 1, 2,..., n.
Теперь можно показать, что выборочная средняя 
есть несмещенная оценка средней генеральной совокупности или, что то же самое, математического ожидания интересующей нас случайной величины x:
Выведем формулу для дисперсии выборочной средней:
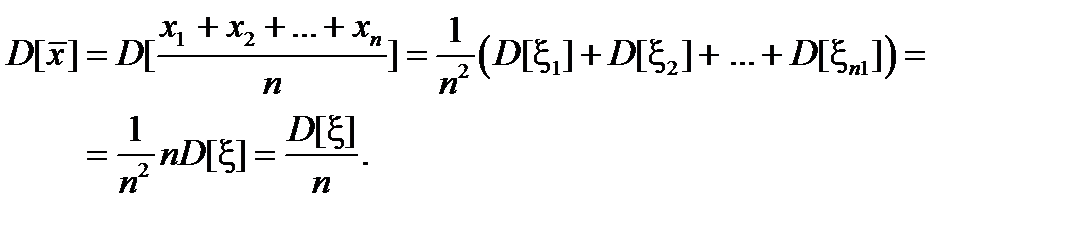
Найдем теперь, чему равно математическое ожидание выборочной дисперсии s 2. Сначала преобразуем s 2 следующим образом:
Здесь использовано преобразование:
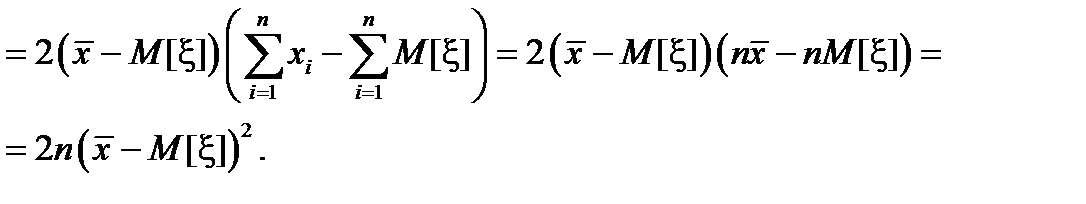
Теперь, используя полученное выше выражение для величины s 2, найдем ее математическое ожидание.
Так как M [s2] ¹ D [x], то выборочнаядисперсияне является несмещенной оценкойдисперсии генеральной совокупности.
Чтобы получить несмещенную оценку дисперсии генеральной совокупности, нужно умножить выборочную дисперсию на 
. Тогда получится величина
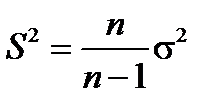или 
называемая исправленной выборочной дисперсией.
Пусть имеется ряд несмещенных точечных оценок одного и того же параметра генеральной совокупности. Та оценка, которая имеет наименьшую дисперсию, называется эффективной.
Полученная из выборки объема n точечная оценка d n параметра D генеральной совокупности называется состоятельной, если она сходится по вероятности к D. Это означает, что для любых положительных чисел e и g найдется такое число n eg, что для всех чисел n, удовлетворяющих неравенству n > n eg выполняется условие
и 
являются несмещёнными, состоятельными и эффективными оценками величин D [x] и M [x].
Пример 28. Приведенная ниже таблица представляет собой случайную выборку значений признака X. Объем выборки n =100.
| 50,2 | 54,0 | 41,0 | 42,0 | 58,2 | 59,3 | 84,8 | 45,0 | 76,5 | 58,3 |
| 21,0 | 55,0 | 45,0 | 21,5 | 46,0 | 44,0 | 42,5 | 49,0 | 48,7 | 75,0 |
| 15,3 | 55,0 | 23,8 | 46,5 | 53,0 | 62,8 | 78,5 | 67,0 | 34,5 | 49,9 |
| 49,7 | 63,0 | 30,0 | 32,0 | 42,4 | 22,4 | 52,0 | 70,4 | 57,2 | 50,0 |
| 23,0 | 47,8 | 47,4 | 50,8 | 78,3 | 27,0 | 56,6 | 51,3 | 58,6 | 28,4 |
| 51,7 | 50,0 | 48,8 | 49,4 | 57,5 | 47,4 | 33,5 | 27,0 | 39,7 | 57,5 |
| 18,4 | 35,6 | 28,4 | 37,6 | 49,5 | 26,7 | 54,0 | 68,6 | 29,3 | 62,7 |
| 43,8 | 44,0 | 69,1 | 46,3 | 76,7 | 37,1 | 69,2 | 39,3 | 30,0 | 43,0 |
| 85,0 | 63,0 | 30,0 | 43,8 | 64,8 | 22,0 | 38,8 | 42,3 | 64,8 | 41,0 |
| 30,0 | 10,0 | 63,0 | 48,8 | 71,2 | 54,4 | 47,8 | 31,2 | 46,1 | 17,8 |
Найти закон распределения, точечные оценки математического ожидания, дисперсии и среднеквадратического отклонения признака X.
Решение. Значения Х в таблице почти не повторяются, поэтому построим интервальное распределение Х. Определим длину каждого частичного интервала (In), предварительно найдя по таблице размах выборочных значений (R):
, 
,
где n =100 – объем выборки.
Нижняя граница первого интервала принимается равной 
а его верхнюю границу 
второй интервал будет (15; 25), третий (25; 35) и так далее. Если повторяющееся выборочное значение совпадает с границей двух соседних интервалов, то договоримся относить его к левому интервалу. Так число 55 дважды будет отнесено к интервалу (45; 55) и ни разу – к интервалу (55; 65).
В итоге этих действий получаем следующее интервальное распределение исходной выборки, куда внесены не только частоты 
, но и относительные частоты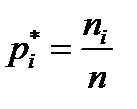 
выборочных значений признака, попавшего в i -й частичный интервал:
| xi –1– xi | 5-15 | 15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | 75-85 |
| ni | ||||||||
| 0,01 | 0,09 | 0,14 | 0,19 | 0,29 | 0,15 | 0,07 | 0,06 |
Для проверки правильного заполнения таблицы нужно убедиться, что сумма элементов второй строки равна объему выборки (в нашем примере n =100), а сумма элементов третьей строки равна единице.
Распределение непрерывной случайной величины характеризуется функцией плотности вероятностей. В статистике ее оценкой является гистограмма относительных частот. Это ступенчатая фигура, для построения которой по горизонтальной оси откладываются частичные интервалы, по вертикальной – плотности относительных частот 
В нашем примере
| 0,001 | 0,009 | 0,014 | 0,019 | 0,029 | 0,015 | 0,007 | 0,006 |
От интервального распределения выборки можно перейти к точечному (дискретному) распределению, взяв за новые выборочные значения признака середины частичных интервалов. В рассматриваемом примере такое распределение будет иметь вид следующей таблицы:
| xi | ||||||||
| ni | ||||||||
| 0,01 | 0,09 | 0,14 | 0,19 | 0,29 | 0,15 | 0,07 | 0,06 |
Для наглядности можно построить полигон относительных частот. Это ломаная линия, вершины которой находятся в точках (xi, 
).
Для точечного распределения выборки можно построить эмпирическую функцию распределения F* (x). Она является статистической оценкой функции распределения вероятностей признака Х (интегрального закона распределения) и строится по формуле 
, где n – объем выборки, а nх – сумма частот выборочных значений признака Х, меньших х. Ясно, что эмпирическую функцию распределения характеризует процесс накопления относительных частот. В нашем примере
Аналогом эмпирической функции распределения является кумулята относительных частот, представляющую собой для точечного (дискретного)выборочного распределения ломаную линию с вершинами в точках 
, где n – объем выборки, а nх – сумма частот выборочных значений признака Х, меньших хi.
Точечные статистические оценкигенеральных параметров распределения признака Х вычислим по формулам
где xi – выборочное значение признака Х, ni – частоты этих значений, n – объем выборки.
Получим
