Интервальные оценки. Доверительные интервалы для параметров нормального распределения

 

Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных. Их недостаток заключается в том, что неизвестно, с какой точностью оценивается параметр. Если для выборок большого объема точность обычно бывает достаточной (при условии несмещенности, эффективности и состоятельности оценок), то для выборок небольшого объема вопрос точности оценок становится очень важным.

Введем понятие интервальной оценки неизвестного параметра генеральной совокупности (или случайной величины x, определенной на множестве объектов этой генеральной совокупности). Обозначим этот параметр через D.

По сделанной выборке по определенным правилам найдем числа D₁ и D₂, так чтобы выполнялось условие:

P (D₁< D < D₂) =P (DÎ(D₁; D₂)) = g.

Числа D₁ и D₂ называются доверительными границами, интервал (D₁, D₂) – доверительным интервалом для параметра D. Число g называется доверительной вероятностью или надежностью сделанной оценки.

Сначала задается надежность. Обычно ее выбирают равной 0.95, 0.99 или 0.999. Тогда вероятность того, что интересующий нас параметр попал в интервал (D₁, D₂) достаточно высока.

Число (D₁ + D₂)/2 – середина доверительного интервала – будет давать значение параметра D с точностью (D₂ – D₁)/2, которая представляет собой половину длины доверительного интервала.

Границы D₁ и D₂ определяются из выборочных данных и являются функциями от случайных величин x ₁, x ₂,..., x_n , а следовательно – сами случайные величины.

Отсюда – доверительный интервал (D₁, D₂) тоже случаен. Он может покрывать параметр Dили нет. Именно в таком смысле нужно понимать случайное событие, заключающееся в том, что доверительный интервал покрывает число D.

 

Доверительный интервал для математического ожидания
нормального распределения при известной дисперсии

Пусть случайная величина x (определенная на множестве объектов генеральной совокупности) распределена по нормальному закону, для которого известна дисперсия D [x] = s² (s > 0). Из генеральной совокупности делается выборка объема n: 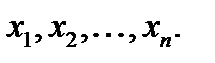Чтобы подчеркнуть случайный характер величин 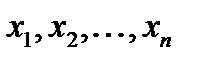, будем рассматривать их как совокупность n независимых случайных величин, распределенных так же, как ξ:

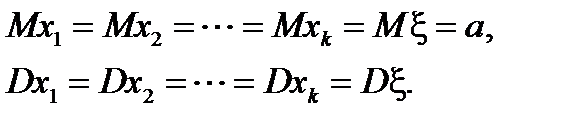
Можно доказать, что случайная величина 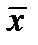(выборочное среднее) также распределена по нормальному закону с математическим ожиданием M 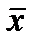= M x = a и дисперсией 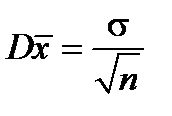, т.е.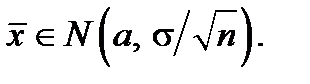

Обозначим неизвестную величину M x через a и подберем по заданной надежности gчисло Δ > 0 так, чтобы выполнялось условие:

P (| – a | < Δ) =g. (7)

Как известно, вероятность того, что случайная величина 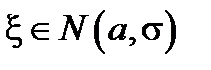принимает значение в интервале (a –l, a +l), симметричном относительно центра рассеяния a, вычисляется по формуле:

Используя вышеприведенную формулу, получаем

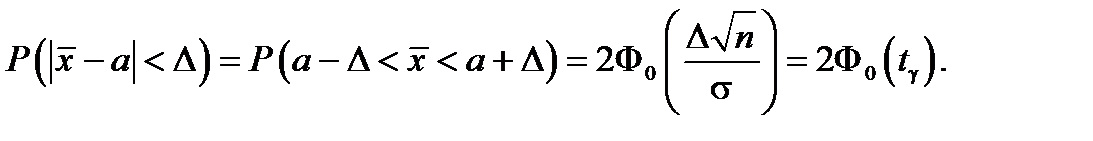
Осталось подобрать Δ так, чтобы выполнялось равенство

Для любого gÎ [0; 1] по таблице «Значение функции Лапласа» можно найти аргумент (число t _g), чтобы F₀(t _g) =g/2.

Теперь из равенства 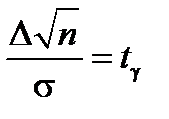определим значение Δ:

.

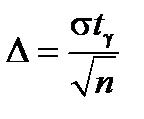Окончательный результат получим, представив формулу (7) в виде:

.

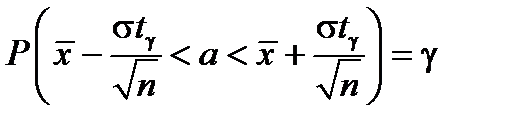Смысл последней формулы состоит в следующем: с надежностью g доверительный интервал

покрывает неизвестный параметр a = M xгенеральной совокупности.

Можно сказать иначе: точечная оценка 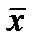определяет значение параметра M x с точностью 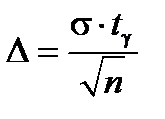и надежностью g.

Пример 29. Среднее содержание вредных примесей, определенных на основании выборки, равно 18,307 мг; найти доверительный интервал для а – истинного содержания вредных примесей с надежностью (1–α)=0,95. Среднее квадратическое отклонение известно и равно σ = 0,0029 мг. Объем выборки n =5.

Решение. Учитывая, что g = (1–α) = 0,95 и F₀(t _g) =g/2 = 0.475, по таблице «значение функции Лапласа» выясняем, что t _g=1,96. Тогда предельная погрешность интервального оценивания

Искомый доверительный интервал равен

18.307–0.0025 < а < 18.307+0.0025, или 18.3015 < а < 18.3095.

Следуя полученному результату, можно утверждать, что если будет произведено достаточно большое число выборок, то только в 5 случаях из 100 содержание вредных примесей может выйти за границы доверительного интервала.

 

Доверительный интервал для математического ожидания
нормального распределения при неизвестной дисперсии

Пусть x – случайная величина, распределенная по нор­мальному закону с неизвестным математическим ожиданием M x(которое обозначим буквой a) и неизвестным σ. Произведем выборку объема n. Определим среднюю выборочную и исправленную выборочную дисперсию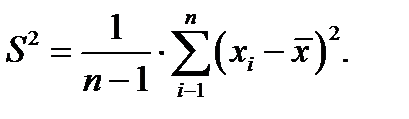

Рассмотрим случайную величину 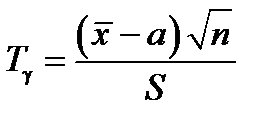, которая (доказывается) будет распределена по закону Стьюдента с
(n – 1) степенями свободы.

Задача заключается в том, чтобы по заданной надежности g и по числу степеней свободы (n – 1) найти такое число T _g, чтобы выполнялось равенство

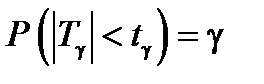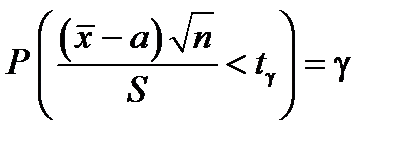или , (8)

или эквивалентное равенство

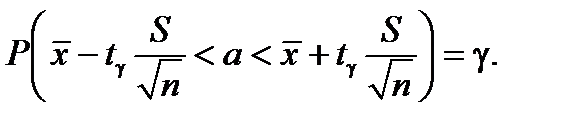
Здесь в скобках – условие того, что значение неизвестного параметра a принадлежит некоторому промежутку, который и является доверительным интервалом. Его границы зависят от надежности g, а также от параметров выборки 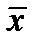и S.

Чтобы определить значение t_g по величине g, равенство (8) преобразуем к виду:

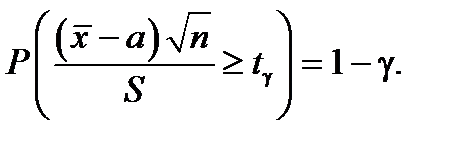
Теперь по таблице «Квантили распределения Стьюдента» для случайной величины t _g, распределенной по закону Стьюдента, по вероятности 1 – g и числу степеней свободы n – 1 находим t _g и, следовательно, искомый доверительный интервал:

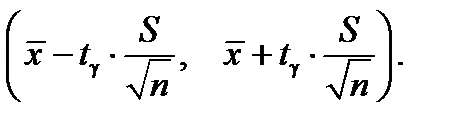
Пример 30. По условию примера 29, найти для истинного содержания вредных примесей доверительный интервал с надежностью 0,95, считая неизвестной дисперсию генеральной совокупности. Рассчитанное по выборке исправленное среднее квадратическое отклонение S = 0,0029 мг.

Решение. По таблице «Квантили t – распределения Стьюдента» определим критические точки по заданной доверительной вероятности g = (1–α) = 0,95 и числу степеней свободы k = n – 1 = 5 – 1 = 4. Получим t _g = 2,78. Вычислим предельную погрешность интервального оценивания

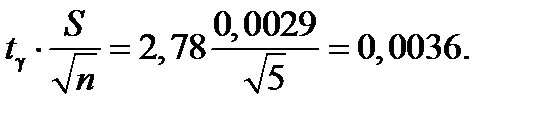
Искомый доверительный интервал равен

18.307–0.0036 < а < 18.307+0.0036, или 18.3034 < а < 18.3106.

Сравнивая доверительные интервалы, накрывающие с одной и той же доверительной вероятностью 0,95 истинное содержание вредных примесей, в случае, когда генеральная дисперсия известна и когда неизвестна, видим, что во втором случае доверительный интервал получается более широкий. Однако при объеме выборки n > 30 эти отличия станут незначительными.

 

Доверительный интервал для дисперсии нормального
распределения

Пусть случайная величина x распределена по нормальному закону, для которого математическое ожидание M x = a идисперсия 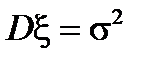неизвестны. Делается выборка объема n. Из нее определяется исправленная выборочная дисперсия 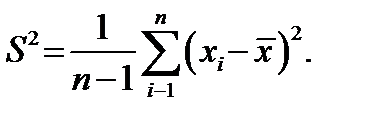Вводим случайную величину , распределенную по законуc²c (n –1) степенями свободы.

По заданной надежности g можно найти сколько угодно границ c₁² и c₂² интервалов, таких, что

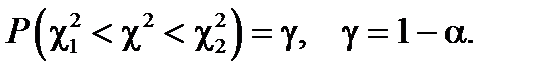
Найдем c₁² и c₂² из следующих условий:

(9)   (10)

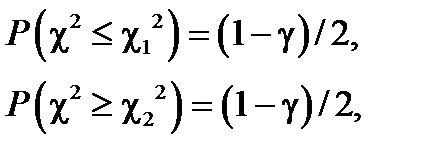
В таблице «Квантили 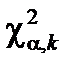распределения 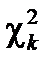» для случайной величины c² обычно дается решение уравнения
P (c² ³ c_α²) = α. Из такой таблицы по заданной величине α и по числу степеней свободы n – 1 можно определить значение c_α². Таким образом, сразу находится значение c₂² в формуле (10).

Для определения c₁² преобразуем (9):

P (c² ³ c₁²) = 1 – (1 – g)/ 2 = (1 + g)/ 2.

Полученное равенство позволяет определить по названной таблице значение c₁².

Теперь, когда найдены значения c₁² и c₂², представим исходное равенство в виде . Или

Последнее равенство перепишем в такой форме, чтобы были определены границы доверительного интервала для неизвестной величины D x:

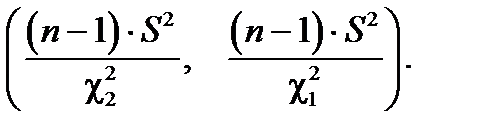
Здесь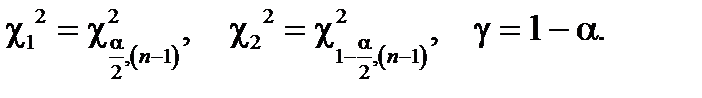

Если математическое ожидание M x = a известно, то доверительный интервал для неизвестной величины D x будет иметь вид:

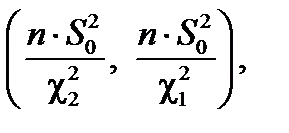где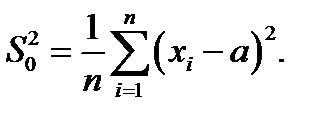

 

Пример 31. Приняв числовые данные примера 29, найти доверительный интервал, накрывающий неизвестное среднеквадратическое отклонение σ с заданной надежностью 0,95.

Решение. По таблице «Квантили 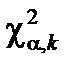распределения » найдем значения хи-квадрат с k степенями свободы k = n –1=4. Будем иметь 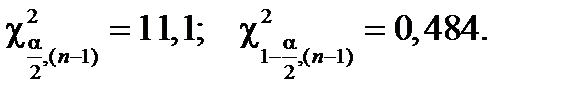Тогда искомый доверительный интервал 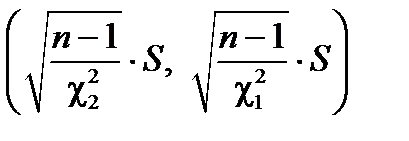имеет вид:

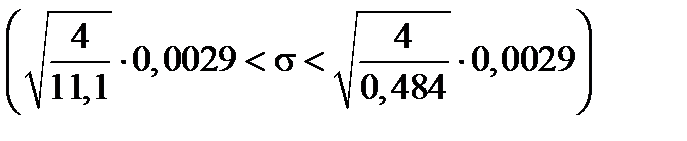, или 0,0017 < σ < 0,0084.