В основе математики лежит понятие множества. Природа элементов абстрактного множества нас не интересует. От элементов требуется только одно, чтобы они подчинялись заданной системе аксиом. Ценность формального определения состоит в том, что оно выявляет общие свойства совершенно, казалось бы, различных математических объектов. Например, числовые множества имеют одинаковые алгебраические свойства. Напомним эти множества.
Натуральные числа. Леопольд Кронекер когда-то произнес: «Натуральное число создал господь Бог, все прочие – дело рук человеческих». Натуральный ряд – это числа 1, 2, 3 и т.д. до бесконечности. Обозначение натурального ряда: 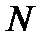 .
.
Целые числа – это числа вида n, – n и 0, где n – натуральное число. Все целые числа можно записать так: …, –2, –1, 0, 1, 2, … Отсюда следует, что любое натуральное число является также и целым. Обозначение:  .
.
Рациональные числа – это числа вида p/q, где p и q – целые числа, причем q ≠ 0. Обозначение:  . Очевидно, что любое целое число является рациональным.
. Очевидно, что любое целое число является рациональным.
Действительные или вещественные числа (или континуум) получают из рациональных чисел с помощью некоего предельного процесса. Это наши обычные числа. Обозначение:  . Рациональное число всегда действительное. Таким образом,
. Рациональное число всегда действительное. Таким образом,
 .
.
Иррациональные числа. Любая обыкновенная дробь может быть записана в виде бесконечной периодической десятичной дроби. И наоборот, любая бесконечная периодическая десятичная дробь представляет собой десятичную запись некоторой обыкновенной дроби. А какой смысл могут иметь бесконечные непериодические дроби?
Легко показать, что никакая дробь p / q не может быть корнем уравнения x 2 – 2 = 0. Таким образом  не является рациональным числом, то есть бесконечной периодической десятичной дробью. Действительные, но не рациональные числа называются иррациональнымичислами. Обозначение: J.
не является рациональным числом, то есть бесконечной периодической десятичной дробью. Действительные, но не рациональные числа называются иррациональнымичислами. Обозначение: J.
Комплексные числа. Не каждый многочлен с целыми коэффициентами имеет корни среди действительных чисел, например, квадратный двучлен x 2 + 1. Добавим к действительным числам некое число i, квадрат которого равен –1: i 2 = –1. Число i =  называется мнимой единицей.
называется мнимой единицей.
Полученный таким образом набор чисел вместе с результатами арифметических операций над ними называется комплексными числами:  .
.
Комплексные числа записывают в виде z = x + iy, где x и y – вещественные числа, i – мнимая единица.
x = Re z называется вещественной частью комплексного числа z, y = Im z – мнимой частью.
Комплексно сопряженными называются числа, отличающиеся только знаком своей мнимой части z* = x – iy.
Действительные числа – частный случай комплексных при y = 0. Не действительные числа, т. е. комплексные при y ≠0, называются мнимыми.
Любой многочлен с коэффициентами из  имеет корень в
имеет корень в  .
.
Комплексные числа наглядно изображают на координатной плоскости: на горизонтальной оси лежат вещественные числа Re z, а на вертикальной – мнимые числа Im z.
Модуль числаz равен расстоянию точки, изображающей это число от начала координат  .
.
Для комплексных чисел следующим образом определены операции сложения и умножения:
(х 1, у 1) + (х 2, у 2) = (х 1+ х 2, у 1 + у 2),
(х 1, у 1) × (х 2, у 2) = (х 1· x 2– у 1· у 2, х 1· у 2+ х 2· у 1).
Частное комплексных чисел равно комплексному числу
 .
.
Операции сложения и умножения комплексных чисел обладают свойствами:
коммуникативности: z 1 + z 2 = z 2 + z 1, z 1 · z 2 = z 2 · z 1;
ассоциативности: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3),
(z 1 · z 2) · z 3 = z 1 · (z 2 · z 3);
дистрибутивности: z 1 · (z 2 + z 3) = z 1· z 2 + z 1 · z 3.
Два комплексных числа z 1 = (х 1, у 1) и z 2 = (х 2, у 2) равны, если х 1 = х 2 и у 1 = у 2.
Существует три формы представления комплексного числа z =(x, y):
алгебраическая z = x + iy,
тригонометрическая z =│ z │(cosφ+ i sinφ),
показательная z = │ z │exp(i φ).
Здесь символ exp(i φ) обозначает комплексное число (cosφ+ i sinφ), φ называется аргументом (аrg z) комплексного числа и является решением системы уравнений

Все аргументы различаются на целые кратные 2p и обозначаются единым символом Arg z.
Комплексные числа часто встречаются в качестве корней полиномов.
Многочленом (полиномом)n -й степени называется выражение вида: 
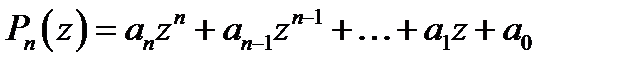 ,
,
где 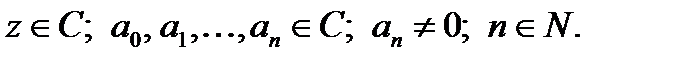
Два многочлена  и
и  равны, если
равны, если
 .
.
Многочлены можно складывать, перемножать, делить.
Существуют единственные многочлены 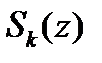 и
и  такие, что
такие, что
 или
или  ,
,
здесь 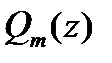 – ненулевой многочлен;
– ненулевой многочлен; 
 или
или  ;
;  .
.
 называют частным от деления
называют частным от деления 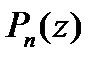 на
на  , а
, а  – остатком.
– остатком.
Если  , то
, то 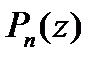 делится на
делится на  без остатка.
без остатка.
Число  называется корнем многочлена
называется корнем многочлена  , если
, если  .
.
Теорема Безу. Остаток от деления многочлена на  равняется значению этого многочлена в точке
равняется значению этого многочлена в точке  .
.
Основная теорема алгебры (теорема Гаусса). Всякий многочлен ненулевой степени имеет по крайней мере один корень.
Пример 2. Решить уравнение z 3 = 1. Найти модули корней. Отобразить на декартовой плоскости решение уравнения.
Решение.

Здесь  – мнимая единица.
– мнимая единица.

1.4 ЛИНЕЙНЫЕ ПРОСТРАНСТВА Rn.
ВЕКТОРЫ И ОПЕРАЦИИ НАД НИМИ.
КООРДИНАТЫ ВЕКТОРА В ЗАДАННОМ БАЗИСЕ
С помощью системы координат удается отождествить вектор или (точку) на плоскости с упорядоченной парой действительных чисел, а в пространстве – с тройкой чисел. Современная физика имеет дело с четырехмерным пространством, где четвертая координата – время. Отвлекаясь от реальных геометрических представлений, можно рассмотреть упорядоченный набор из n действительных чисел 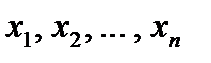 и по аналогии назвать его n-мернымвектором. Числа
и по аналогии назвать его n-мернымвектором. Числа  называются координатами вектора
называются координатами вектора  . Количество координат вектора называется размерностью.
. Количество координат вектора называется размерностью.
Можно исходить и из понятия множества. Декартово произведение множества действительных чисел R само на себя состоит из всевозможных упорядоченных числовых пар и его можно отождествить с плоскостью. Это множество обозначают R 2. Множество R ´ R ´ R = R 3состоит из упорядоченных троек и представляет собой трехмерное пространство. Если осуществить декартово произведение R само на себя n раз, то получим совокупность всех n -мерных векторов – пространство Rn.
Чтобы работать с математическими объектами, необходимо определить операции над ними. Операции над n -мерными векторами вводятся по аналогии с обычными и обладают теми же алгебраическими свойствами. Напомним их:


 ;
;  ;
;


 ;
; 
Всякое множество, для элементов которого определены операции сложения и умножения элементов на число таким образом, что выполняются вышеперечисленные свойства, называется векторным пространством.
На случай n -мерного пространства Rn:
пусть  . Тогда
. Тогда


Скалярным произведением двух векторов называется число
 .
.
Аналогично длине вектора в трехмерном пространстве определяется норма вектора  в Rn - пространстве:
в Rn - пространстве:

Линейная независимость. Базис
Система векторов  будет называться линейно зависимой, если найдется набор чисел l1, l2,…, l k, не все из которых равны нулю, такой, что выполняется равенство
будет называться линейно зависимой, если найдется набор чисел l1, l2,…, l k, не все из которых равны нулю, такой, что выполняется равенство
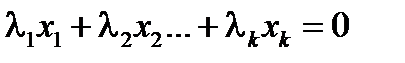 .
.
В противном случае (т.е.  ) система
) система  называется линейно независимой.
называется линейно независимой.
Два ненулевых вектора на плоскости линейно независимы тогда и только, когда они неколлинеарны.
Любые три вектора на плоскости линейно зависимы.
Аналогично для трех- и четырехмерного пространства.
Вообще, любые n +1 векторов пространства Rn линейно зависимы. Так, легко проверить, что система векторов

линейно независима.
Пусть  – произвольный вектор. Тогда, очевидно, справедливо равенство
– произвольный вектор. Тогда, очевидно, справедливо равенство

Говорят, что вектор  разложен по векторам
разложен по векторам  Эта система векторов называется базисом пространства Rn.
Эта система векторов называется базисом пространства Rn.
Любые n линейно независимых векторов Rn образуют базис, причем любые m < n линейно независимых векторов базиса Rn не образуют. Таким образом, минимальное количество векторов, которые могут составить базис Rn , равно n.
Вектор в косоугольном базисе трех векторов
Пусть задано 4 вектора 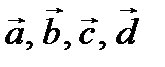
 в декартовой системе координат. Тогда вектор
в декартовой системе координат. Тогда вектор  в базисе
в базисе  может быть представлен в виде:
может быть представлен в виде:  .
.
Если расписать это векторное равенство, то получим систему линейных алгебраических уравнений

По правилу Крамера (см. параграф ниже) можно найти коэффициенты разложения  ; i = 1, 2, 3.
; i = 1, 2, 3.






