Краеугольным камнем современной математики является теория множеств.Ее основателями в 19 веке явились Больцана, Кантор, Дедекинд. Бурбаки утверждали, что возможно вывести всю математику из единого источника – теории множеств.
Для теоретиков множественная аксиоматика является фундаментом современной теории вероятностей и других разделов.
Понятие множества вводится аксиоматически. Множество определяет совокупность объектов произвольной природы.
Множество – любое собрание, коллекция любых объектов. Обозначение: прописные латинские буквы A, B, C …
Элемент множества – любой объект множества: а Î A. Обозначение не принадлежности: i Ï A.
Два множества равны в том и только в том случае, когда они состоят из одних и тех же элементов.
При записи математических рассуждений используют экономную символику, применяемую в логике.
Cлово «любые» заменяется символом " – квантором всеобщности, а слово «существует» – символом $ – квантором существования.
Запись " x Î X a(x)означает, что для всякого элемента x Î X истинно утверждение a(x).
Запись $ x Î X a(x)означает, что существует элемент x Î X такой, что для него истинно утверждение a(x).
Если элемент x Î X, для которого истинно утверждение a(x), не только существует, но и единственен, то пишут
$! x Î X a(x).
Множество конечно, если оно содержит натуральное или нулевое число элементов, и бесконечно, если оно не является конечным.
Множество X называется ограниченным сверху, если существует действительное число а такое, что х £ а для всех x Î X. Всякое число, обладающее этим свойством, называется верхней гранью множества X.
Для заданного ограниченного сверху множества X множество всех его верхних граней имеет наименьший элемент, который называется точной верхней гранью множества X и обозначается символом sup X.
Точная нижняя грань множества X обозначается символом inf X.
Множество X, ограниченное сверху и снизу, называется ограниченным.
К примеру, множество [0, 1) имеет множество верхних граней [1, +¥), наименьший элемент которого равен 1. Поэтому sup[0, 1)=1, причем 1Ï[0, 1); inf[0, 1)=0.
Множество A называется подмножеством множества B, или множество A принадлежит множеству B, если " элемент A принадлежит также и B. Обозначение: A Ì B.
Множество A не принадлежит множеству B, если $ x: x Î A и x Ï B. Обозначение: A Ë B.
Пустым множеством,илинуль-множеством, называется множество Æ = {" x: x Ë Æ}
Существует только одно пустое множество.
Подмножества A и Æ множества A называются тривиальными.
Булеаном множества A называется множество всех подмножеств множества A. Обозначается готической буквой
M (A).
Множество задают либо перечислением его элементов, либо описанием свойств его элементов. В последнем случае используется обозначение A= { x Î T:a(x)} или A= { x Î T ça(x)}. То есть множество A – это совокупность тех, и только тех, элементов из некоторого основного множества T, которые обладают свойством a.
Двухэлементное множество{ x, у }, в котором элемент х находится на первом, а элемент у на втором месте, называется упорядоченной парой (x, у).
Элемент х называется первой координатой упорядоченной пары (x, у), а у – второй координатой.
Две упорядоченные пары равны, если совпадают их координаты.
Пусть заданы два множества Х и Y. Множество всевозможных упорядоченных пар { x, у } таких, что x Î Х и у Î Y называется декартовым произведением и обозначается Х ´ Y. Например, декартовым произведением является плоскость с двумя координатными осями, так как определяет множество пар вещественных чисел.
Пример 1. Описать перечислением элементов множество 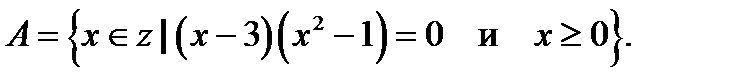
Решение. A есть множество всех целых неотрицательных корней уравнения  . Следовательно,
. Следовательно,