Задача
На двухопорной балке, изготовленной из двух равнобоких уголков №4, установлен электродвигатель, вес которого F=0,4 кН. Число оборотов электродвигателя N=500 об/мин, амплитудное значение центробежной силы, возникающей при вращении ротора, F0=0,05 кН. Произвести проверочный расчет на прочность подмоторной балки и определить значение ℓ, при котором возможно наступление резонанса. Сопротивлением среды пренебречь. Допускаемое напряжение [σ] принять равным 160 МПа.
Решение
Прежде, чем приступить к решению задачи, давайте сначала разберемся, что происходит с упругой балкой при заданном нагружении.
До установки двигателя балка находилась в прямолинейном равновесном состоянии:
После установки двигателя (в выключенном режиме), который можно рассматривать как сосредоточенную массу, балка принимает новое изогнутое равновесное состояние:
При этом, на балку действует статическая нагрузка – вес двигателя 
.
При включенном двигателе к его весу добавляется действие динамической вибрационной возмущающей силы 
, которая по своей природе является центробежной силой, возникающей при вращении ротора от его неуравновешенной части. Эта сила вызывает вынужденные колебания всей упругой системы вокруг изогнутого равновесного состояния:
Направление колебательного движения перпендикулярно осевой линии балки, поэтому колебания являются поперечными. Вид возникающей при этом деформации балки – прямой поперечный изгиб.
Таким образом, расчетная схема балки представляет собой упругую систему с одной степенью свободы, воспринимающую поперечные вынужденные колебания.
Так как вес сосредоточенной массы (двигателя) F по направлению совпадает с направлением колебательного движения, то, согласно пункту 3 приведенного выше алгоритма (стр. 73-74), условие прочности для нашей балки будет иметь вид (7.4):
.
Выполнение этого условия нам и нужно будет проверить.
Приступим, наконец, к непосредственному решению задачи.
1. Определим геометрические характеристики поперечного сечения балки: осевой момент инерции Ix и осевой момент сопротивления Wx, которые нам потребуются при прочностном расчете.
Поперечное сечение сложное – состоит из двух равнобоких уголков №4:
Оси х и у – главные центральные оси сечения, причем, ось у – силовая линия, а ось х – нейтральная линия. По сортаменту (см. Приложение 4, таблица 4.3, стр. 154) для одного равнобокого уголка №4 находим: 
, 
, 
.
По теореме о суммировании моментов инерции (см. Практикум, часть 1, стр. 27) осевой момент инерции всего сложного сечения равен:
.
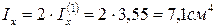Осевой момент сопротивления Wx находим по определению (см. Практикум, часть 1, стр. 34):
.
2. Найдем максимальное статическое напряжение 
от статического действия силы, равной весу двигателя . Для этого построим грузовую эпюру изгибающих моментов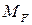 
(балка испытывает прямой изгиб) и определим положение опасного сечения.
Максимальный изгибающий момент 
возникает в сечении С, следовательно, сечение С наиболее опасно. Тогда
.
Таким образом, при выключенном двигателе максимальное напряжение возникает в сечении С балки и равно 
.
3. Найдем максимальное статическое напряжение 
от статического действия силы 
, равной амплитудному значению вынуждающей динамической силы . Рассуждения здесь аналогичные, как и в пункте 2, единственное отличие в том, что вместо силы F в сечении С прикладывается сила . Эпюра изгибающих моментов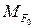 
будет пропорциональна грузовой эпюре 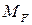, а максимальный изгибающий момент 
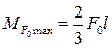. Тогда
.
4. Найдем коэффициент усиления колебаний 
.
4.1. Определим податливость упругой системы 
. Учитывая, что это единичное перемещение, определим его методом Мора. Для этого приложим в точке С в направлении колебательного движения единичную безразмерную сосредоточенную силу и построим единичную эпюру изгибающих моментов 
. Очевидно, что она тоже будет пропорциональна грузовой эпюре 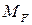с коэффициентом пропорциональности F. «Перемножив» единичную эпюру саму на себя, получим искомую величину .
Единичная эпюра имеет два участка: АС и СВ. Применяя формулу Симпсона на каждом участке, получим:
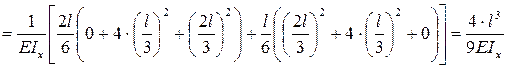. (7.5)
4.2. Вычислим частоту собственных колебаний 
по формуле (7.2), учитывая, что масса двигателя 
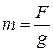, и принимая 
:
.
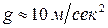4.3. Вычислим частоту вынужденных колебаний 
по заданному числу оборотов электродвигателя N:
.
4.4. Коэффициент усиления колебаний найдем по формуле (7.1):
.
5. Проверим выполнение условия прочности.
Подставим найденные значения всех величин в условие прочности и проверим его выполнение.
.
Таким образом, 
, следовательно, условие прочности выполняется.
6. Определим значение параметра длины балки lр, при котором возможно наступление резонанса.
Условие резонанса, как отмечалось выше – это равенство частот вынужденных и собственных колебаний упругой системы: 
. Частота вынужденных колебаний не зависит от значения параметра l, а частота собственных колебаний связана с параметром l полученной ранее зависимостью (7.5):
.
Подставим это выражение в условие резонанса:
.
Возведем обе части равенства в квадрат и выразим параметр lр:
.
Таким образом, при 
в заданной конструкции будет наблюдаться явление резонанса, что может привести к её разрушению.
Внимание! 
При проектировании подобных конструкций следует избегать резонансных значений её параметров.
Задача решена. 
