Стойка длиной ℓ=1 м с шарнирно опертыми концами и промежуточной шарнирной опорой посередине сжимается силой F=20 кН.
Требуется:
a). Подобрать величину размера «а» поперечного сечения стойки с использованием коэффициента продольного изгиба 
, обеспечив ее устойчивость, если допускаемое напряжение на сжатие [σ]с=160 МПа.
b). Для спроектированной стойки определить величину критической силы и коэффициент запаса устойчивости.
Решение:
a). Определим допускаемую величину характерного размера поперечного сечения стойки.
Данная задача относится к классу проектировочных и решается методом последовательных приближений.
1. Выразим необходимые для расчета геометрические характеристики поперечного сечения через характерный размер «а». Моменты инерции:
Из этих результатов видно, что ось х является осью наименьшей жесткости и поэтому выразим через «а» радиус инерции относительно оси х:
,
где А – площадь поперечного сечения:
.
Тогда
.
2. Итерация №1. Зададим первое значение коэффициента продольного изгиба 
.
3. Определим допускаемую величину площади поперечного сечения
.
4. Определим характерный размер
и минимальный радиус инерции
.
5. Определим максимальную гибкость стойки
.
6. Из таблицы коэффициента продольного изгиба (см. Приложение 4, таблица 4.6, стр.158) по найденной гибкости и марке материала выпишем уточненный коэффициент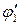 
. Полученная гибкость попала по таблице в интервал значений 90-100. Фрагмент таблицы для Ст3:
Для определения значения 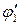проведем линейную интерполяцию:
.
7. Сравним значения 
и 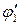, т.е. значение 0,5 и 0,6144. Расхождение в десятых долях считается существенным и составляет
,
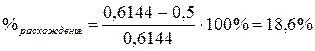что требует продолжения расчета (приближения). Для этого подготовим для следующей итерации коэффициент
и перейдем к расчету на второй итерации, начиная с пункта 3 алгоритма.
Итерация №2
; 
;
;
.
Гибкость попала в интервал значений 100-110. Фрагмент таблицы для этого интервала (см. Приложение 4, таблица 4.6, стр.158):
И вновь проведем линейную интерполяцию для определения 
:
.
Оценим % расхождения между и 
:
и это уже небольшое расхождение, позволяющее выйти из итерационного процесса.
8. Определим процент погрешности между расчетным (действующим) напряжением в конце 2-й итерации
и допускаемым напряжением [σ]с:
<3%,
т.е. подбор размера поперечного сечения стойки закончен.
b). Определим величину критической силы и коэффициент запаса по устойчивости.
Для определения величины критической силы узнаем, к какому типу относится данная стойка: малой, средней или большой гибкости? С этой целью сравним значение гибкости на последней итерации λmax2=104 c предельными значениями для Ст3 λ0=61 и λпред=100. Т.к. λmax2=104> λпред=100, значит спроектированная стойка обладает большой гибкостью, и расчет критической силы произведем по формуле Эйлера:
Коэффициент запаса по устойчивости
.
Задача решена. 
