Стойка, имеющая поперечное сечение в виде двух швеллеров № 12, нагружена осевой сжимающей нагрузкой F. Материал стойки Ст2 с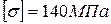 
. Условия закрепления одинаковы в плоскостях xoz и yoz.
Требуется определить:
a). Расстояние «X» между ветвями стойки, обеспечивающее равноустойчивость конструкции.
b). Величину допускаемой нагрузки, используя коэффициент продольного изгиба.
c). Величину критической силы и коэффициент запаса устойчивости.
Решение
a). Для определения расстояния Х, при котором стойка будет равноустойчивой, запишем условие равноустойчивости: 
. Из равенства гибкостей следует, что
,
т.е. приводит в данном случае к равенству моментов инерции. Выпишем из таблицы сортамента прокатных профилей моменты инерции швеллера №12 относительно его главных центральных осей, площадь и расстояние хо (см. Приложение 4, таблица 4.2, стр. 153):
=304 см4, 
=31,2 см4, Ашв=13,3 см2 х0=1,54 см.
Т.к. ось Yшв отстоит от оси Y на расстояние 
, то момент инерции
.
Из условия равноустойчивости 
определим расстояние Х:
.
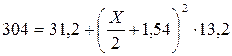
b). Определим величину допускаемой нагрузки. Для этого вычислим гибкость стойки. Т.к. конструкция равноустойчива, то 
. Определим 
, где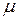 
– коэффициент приведения длины. Для данных условий закрепления 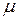=0,5. Радиус инерции из таблицы сортамента для швеллера №12 равен: 
=4,78 см. Тогда
.
По таблице коэффициента продольного изгиба (см. Приложение 4, таблица 4.6, стр. 158) определим величину φ в соответствии с гибкостью и маркой материала. Гибкость попала в интервал значений 70-80. Фрагмент таблицы для этого интервала:
| 
|
| 0,81 | |
| 0,75 |
Определим коэффициент для значения гибкости 
путем линейной интерполяции:
.
Применим формулу для вычисления допускаемой нагрузки:
.
c). Определим величину критической силы. Для этого из справочника выпишем значения 
и 
для Ст2: =60, =105. Гибкость стойки попала в интервал между и , следовательно, стойка относится к области средней гибкости. Величина критической силы рассчитывается по формуле Ясинского:
.
Коэффициенты a и b – справочные величины. Для Ст2 
, 
. Тогда
.
Определим коэффициент запаса устойчивости:
.
Задача решена. 
