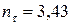с растяжением-сжатием и кручением»
Вариант 1
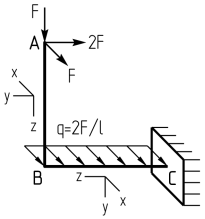
Консольная рама, состоящая из двух элементов одинаковой длины l, изготовлена из пластичного материала и нагружена пространственной системой внешних сил.
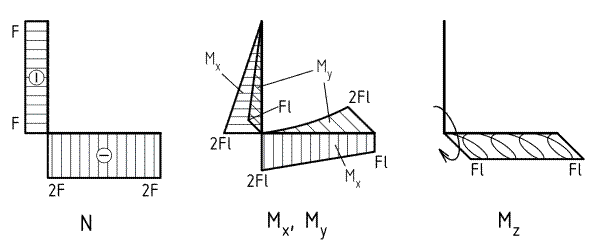
Эпюры внутренних силовых факторов построены:
Поперечное сечение рамы круглое с диаметром d или прямоугольное с соотношением длин сторон h / b = 2 и значениями коэффициентов β = 0,493, γ = 0,795.
Используйте, при необходимости, III теорию предельного состояния.
1. Какое сечение данной рамы является наиболее опасным в случае круглой формы поперечного сечения?
1. Сечение «B» элемента AB
2. Сечение «B» элемента BC
3. Сечение «C»
4. Сечение «B» элемента BC и «C» равноопасны
2. Как располагается силовая линия в плоскости круглого поперечного сечения «C» данной рамы?
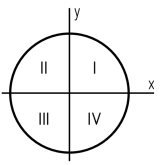
1. Совпадает с осью y
2. Проходит через четверти I и III
3. Совпадает с осью x
4. Проходит через четверти II и IV
3. Какая точка круглого поперечного сечения «C» данной рамы является опасной?
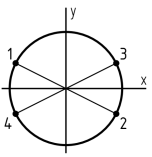
1. Точка «1»
2. Точка «2»
3. Точка «3»
4. Точка «4»
4. Как записывается условие прочности для опасной точки круглого поперечного сечения «C» данной рамы?
1. 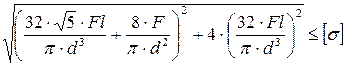
2. 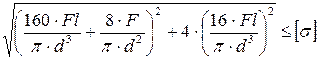
3. 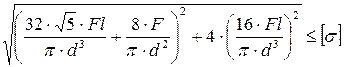
4. 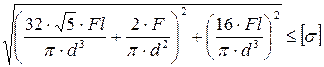
5. Какая форма рамы является более рациональной в случае прямоугольного поперечного сечения?
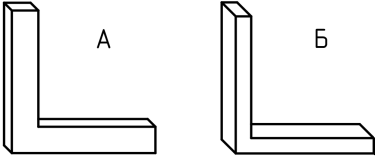
1. «А»
2. «Б»
3. Оба варианта равнозначны
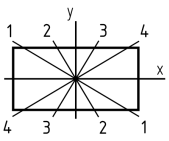
6. Как располагается силовая линия в плоскости прямоугольного поперечного сечения «C» данной рамы?
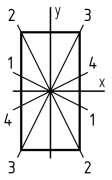
1. 1-1
2. 2-2
3. 3-3
4. 4-4
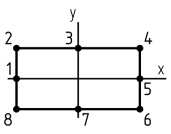
7. Какая тройка точек лежит в опасной четверти прямоугольного поперечного сечения «C» данной рамы?
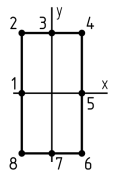
1. Точки «1», «2», «3»
2. Точки «3», «4», «5»
3. Точки «5», «6», «7»
4. Точки «7», «8», «1»
8. Как записывается условие прочности для точки, находящейся в вершине опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
1. 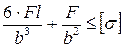
2. 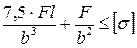
3. 
4. 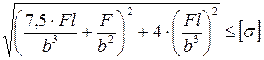
9. Как записывается условие прочности для точки, находящейся посередине длинной стороны в опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
1. 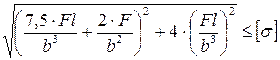
2. 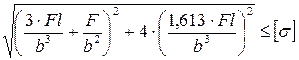
3. 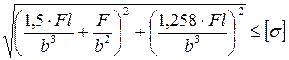
4. 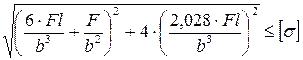
10. Как записывается условие прочности для точки, находящейся посередине короткой стороны в опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
1. 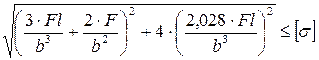
2. 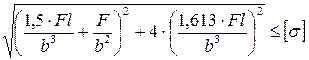
3. 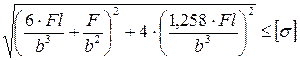
4. 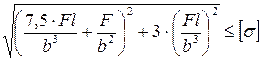
Вариант 2
Консольная рама, состоящая из двух элементов одинаковой длины l, изготовлена из пластичного материала и нагружена пространственной системой внешних сил.
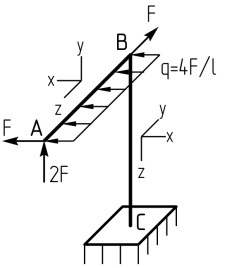
Эпюры внутренних силовых факторов построены:
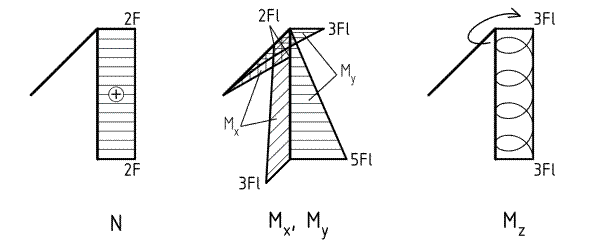
Поперечное сечение рамы круглое с диаметром d или прямоугольное с соотношением длин сторон h / b = 2 и значениями коэффициентов β = 0,493, γ = 0,795.
Используйте, при необходимости, III теорию предельного состояния.
1. Какое сечение данной рамы является наиболее опасным в случае круглой формы поперечного сечения?
1. Сечение «A»
2. Сечение «B» элемента AB
3. Сечение «B» элемента BC
4. Сечение «C»
2. Как располагается силовая линия в плоскости круглого поперечного сечения «C» данной рамы?
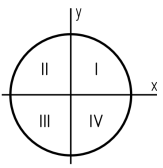
1. Совпадает с осью y
2. Проходит через четверти I и III
3. Совпадает с осью x
4. Проходит через четверти II и IV
3. Какая точка круглого поперечного сечения «C» данной рамы является опасной?
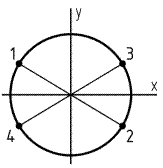
1. Точка «1»
2. Точка «2»
3. Точка «3»
4. Точка «4»
4. Как записывается условие прочности для опасной точки круглого поперечного сечения «C» данной рамы?
1. 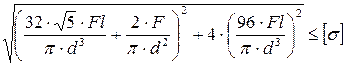
2. 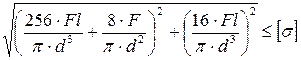
3. 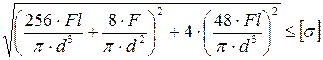
4. 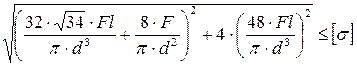
5. Какая форма рамы является более рациональной в случае прямоугольного поперечного сечения?
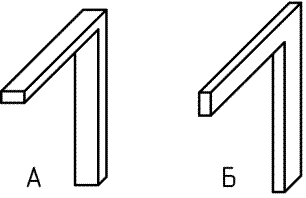
1. «А»
2. «Б»
3. Оба варианта равнозначны
6. Как располагается силовая линия в плоскости прямоугольного поперечного сечения «C» данной рамы?
1. 1-1
2. 2-2
3. 3-3
4. 4-4
7. Какая тройка точек лежит в опасной четверти прямоугольного поперечного сечения «C» данной рамы?
1. Точки «1», «2», «3»
2. Точки «3», «4», «5»
3. Точки «5», «6», «7»
4. Точки «7», «8», «1»
8. Как записывается условие прочности для точки, находящейся в вершине опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
1. в 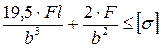
2. 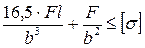
3. 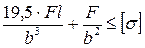
4. 
9. Как записывается условие прочности для точки, находящейся посередине длинной стороны в опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
1. 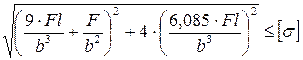
2. 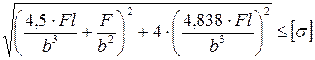
3. 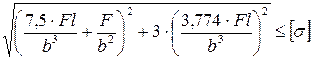
4. 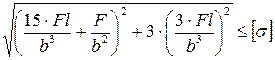
10. Как записывается условие прочности для точки, находящейся посередине короткой стороны в опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
1. 
2. 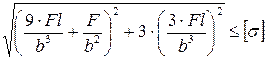
3. 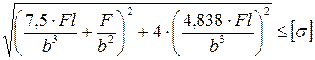
4. 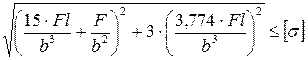
Тесты к теме 5 «Расчет сжатых стоек на устойчивость»
Вариант 1
Для стойки длиной l=50b с заданными условиями закрепления
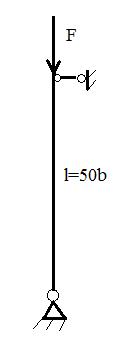
1. Определить величину коэффициента приведения длины 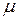 .
.
1. 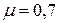
2. 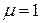
3. 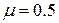
4. 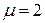
2. Определить, относительно какой оси она обладает максимальной гибкостью, если поперечное сечение прямоугольник со сторонами: 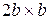 .
.
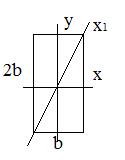
1. 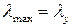
2. 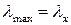
3. 
4. 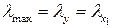
3. Определить величину максимальной гибкости для данного прямоугольного сечения.
1. 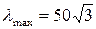
2. 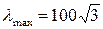
3. 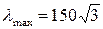
4. 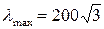
4. Определить, относительно какой оси она обладает максимальной гибкостью, если поперечное сечение квадрат со сторонами 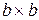 .
.
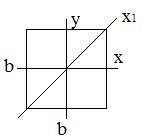
1. 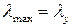
2. 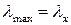
3. 
4. 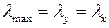
5. 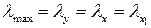
5. Определить величину максимальной гибкости для данного квадратного сечения.
1. 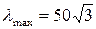
2. 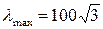
3. 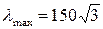
4. 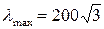
6. Определить соотношение максимальных гибкостей данной стойки для случая прямоугольного сечения со сторонами 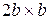 и квадратного сечения со сторонами
и квадратного сечения со сторонами 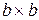 .
.
1. 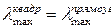
2. 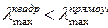
3. 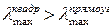
7. Выберите вариант условий закрепления для исходной стойки, чтобы уменьшить ее максимальную гибкость в 2 раза.
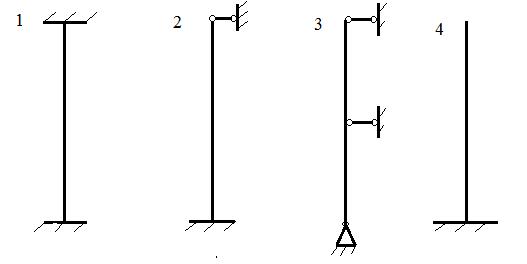
1. 2-й и 3-й варианты
2. 2-й вариант
3. 4-й вариант
4. 1-й и 3-й варианты
8. Какая из приведенных выше стоек имеет минимальный коэффициент приведения длины?
1. 1 и 3
2. 2
3. 4
4. 2 и 3
9. Для какой из вышеприведенных стоек критическая сила, определяемая по формуле Эйлера, имеет минимальное значение, если стойки отличаются только условиями закрепления?
1. 1
2. 2
3. 3
4. 4
10. Методом линейной интерполяции определите с точностью до сотых долей коэффициент снижения основного допускаемого напряжения φ для стойки, обладающей гибкостью λ=93,2, используя справочные данные:
| λ | φ |
| 0,69 | |
| 0,6 |
1. 0,66
2. 0,64
3. 0,68
4. 0,72
Вариант 2
Для сжатого стержня длиной l = 30b с заданными условиями закрепления

l = 30b
1. Определить величину коэффициента приведения длины  .
.
1. 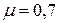
2. 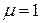
3. 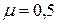
4. 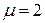
2. Определить величину максимальной гибкости стержня, если его поперечное сечение прямоугольник со сторонами 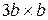 .
.
1. 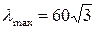
2. 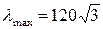
3. 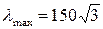
4. 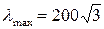
3. Определить величину максимальной гибкости стержня, если его поперечное сечение квадрат со сторонами 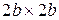 .
.
1. 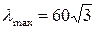
2. 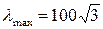
3. 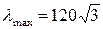
4. 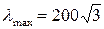
4. Определить соотношение максимальных гибкостей данного стержня для случая прямоугольного сечения со сторонами 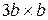 и квадратного сечения со сторонами
и квадратного сечения со сторонами 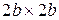 .
.
1. 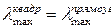
2. 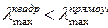
3. 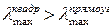
5. Определить соотношение критических сил данного стержня, найденных по формуле Эйлера, для случая прямоугольного сечения со сторонами 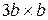 и квадратного сечения со сторонами
и квадратного сечения со сторонами 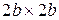 .
.
1. 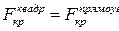
2. 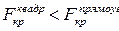
3. 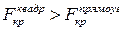
6. Выберите вариант условий закрепления для исходного стержня, чтобы уменьшить его максимальную гибкость в 2 раза.
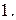

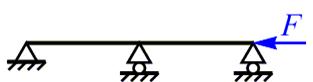

1. 2-й и 3-й варианты
2. 2-й вариант
3. 4-й вариант
4. 1-й и 3-й варианты
7. Какой из приведенных выше стержней имеет минимальный коэффициент приведения длины?
1. 1 и 3
2. 2 и 3
3. 4
4. 2
8. У какого из приведенных выше стержней коэффициент приведения длины 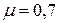 ?
?
1. 1
2. 2
3. 3
4. 4
9. Для какого из вышеприведенных стержней критическая сила, определяемая по формуле Эйлера, имеет минимальное значение, если стержни отличаются только условиями закрепления?
1. 1
2. 2
3. 3
4. 4
10. Методом линейной интерполяции определите с точностью до сотых долей коэффициент снижения основного допускаемого напряжения  для стержня, обладающего гибкостью
для стержня, обладающего гибкостью  =67,7, используя справочные данные:
=67,7, используя справочные данные:

| 
|
| 0,86 | |
| 0,81 |
1. 0,81
2. 0,84
3. 0,82
4. 0,83
Тесты к теме 6 «Расчет на усталостную прочность»
Вариант 1
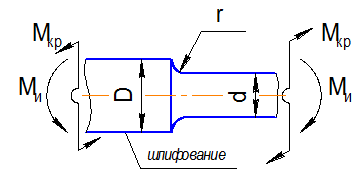
Фрагмент вала с концентратором напряжений в виде галтели испытывает повторно-переменный изгиб с кручением. D=75 мм, d=60 мм, r=5 мм, 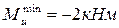 ;
; 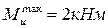 ;
; 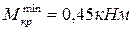 ;
; 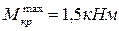 . Вал изготовлен из стали 40ХН с механическими характеристиками:
. Вал изготовлен из стали 40ХН с механическими характеристиками: 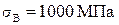 ,
, 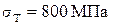 ,
, 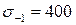 МПа,
МПа,  ,
, 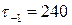 МПа и имеет шлифованную поверхность.
МПа и имеет шлифованную поверхность.
1. Чему равен коэффициент асимметрии цикла нормальных напряжений, возникающих в опасном сечении данного вала?
1. 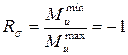
2. 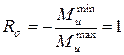
3. 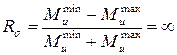
4. 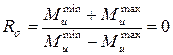
2. Чему равен коэффициент асимметрии цикла касательных напряжений, возникающих в опасном сечении данного вала?
1. 
2. 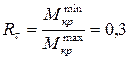
3. 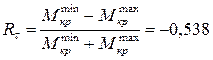
4. 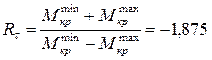
3. Чему равно амплитудное нормальное напряжение цикла в опасном сечении данного вала, если 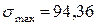 МПа, а
МПа, а 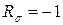 ?
?
1. 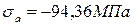
2. 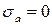
3. 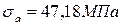
4. 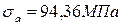
4. Чему равно амплитудное касательное напряжение цикла в опасном сечении данного вала, если 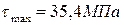 , а
, а  ?
?
1. 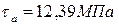
2. 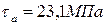
3. 
4. 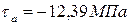
5. Чему равно среднее нормальное напряжение цикла в опасном сечении данного вала, если 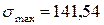 МПа, а
МПа, а 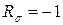 ?
?
1. 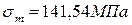
2. 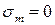
3. 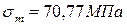
4. 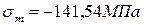
6. Чему равно среднее касательное напряжение цикла в опасном сечении данного вала, если 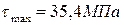 , а
, а  ?
?
1. 
2. 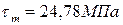
3. 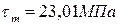
4. 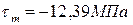
7. Чему равен поправочный коэффициент к амплитудному нормальному напряжению, если коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали, следующие: 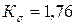 ;
; 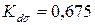 ;
; 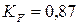 ?
?
1. 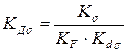 =2,997
=2,997
2. 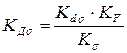 =0,438
=0,438
3.  =0,517
=0,517
4. 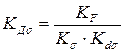 =0,702
=0,702
8. Чему равен поправочный коэффициент к амплитудному касательному напряжению, если коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали, следующие: 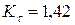 ;
; 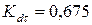 ;
; 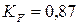 ?
?
1. 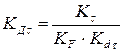 =2,418
=2,418
2. 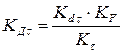 =0,497
=0,497
3. 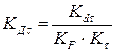 =0,587
=0,587
4. 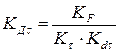 =1,09
=1,09
9. Чему равен коэффициент запаса усталостной прочности по нормальным напряжениям, если 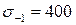 МПа,
МПа, 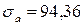 МПа,
МПа, 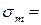 0? Коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали, следующие:
0? Коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали, следующие: 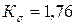 ,
, 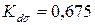 ,
, 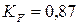 ,
,  .
.
1. 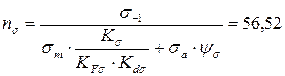
2. 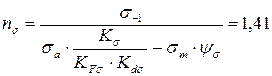
3. 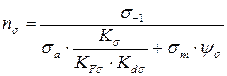 =1,41
=1,41
4. 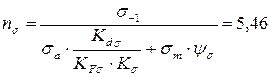
10. Чему равен коэффициент запаса усталостной прочности по касательным напряжениям, если 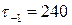 МПа,
МПа, 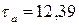 МПа,
МПа, 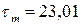 МПа? Коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали по касательным напряжениям, следующие:
МПа? Коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали по касательным напряжениям, следующие: 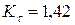 ,
, 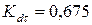 ,
, 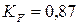 ,
, 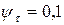 .
.
1. 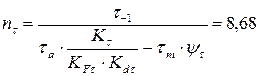
2. 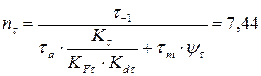
3. 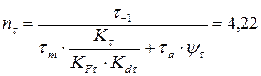
4. 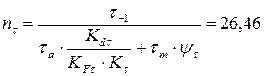
Вариант 2
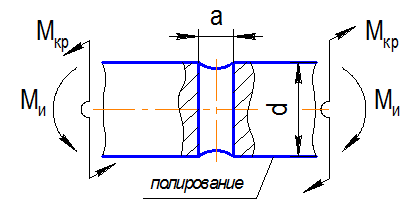
Фрагмент вала с концентратором напряжений в виде сквозного отверстия испытывает повторно-переменный изгиб с кручением. d =70 мм, а =5 мм, 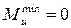 ;
; 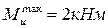 ;
;  ;
; 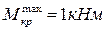 . Вал изготовлен из стали 45 с механическими характеристиками:
. Вал изготовлен из стали 45 с механическими характеристиками: 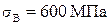 ,
, 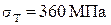 ,
, 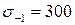 МПа,
МПа, 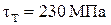 ,
, 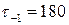 МПа и имеет полированную поверхность.
МПа и имеет полированную поверхность.
1. Чему равен коэффициент асимметрии цикла нормальных напряжений, возникающих в опасном сечении данного вала?
1. 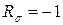
2. 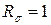
3. 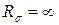
4. 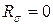
2. Чему равен коэффициент асимметрии цикла касательных напряжений, возникающих в опасном сечении данного вала?
1. 
2. 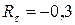
3. 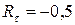
4. 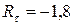
3. Чему равно амплитудное нормальное напряжение цикла в опасном сечении данного вала, если 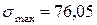 МПа, а
МПа, а 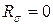 ?
?
1. 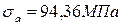
2. 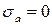
3. 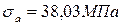
4. 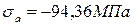
4. Чему равно амплитудное касательное напряжение цикла в опасном сечении данного вала, если 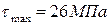 , а
, а 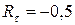 ?
?
1. 
2. 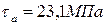
3. 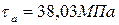
4. 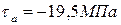
5. Чему равно среднее нормальное напряжение цикла в опасном сечении данного вала, если 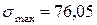 МПа, а
МПа, а 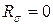 ?
?
1. 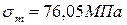
2. 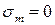
3. 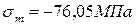
4. 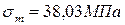
6. Чему равно среднее касательное напряжение цикла в опасном сечении данного вала, если 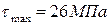 , а
, а 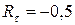 ?
?
1. 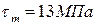
2. 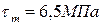
3. 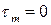
4. 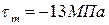
7. Чему равен поправочный коэффициент к амплитудному нормальному напряжению, если коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали, следующие: 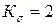 ;
; 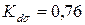 ;
; 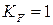 ?
?
1. 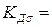 2,63
2,63
2. 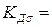 0,38
0,38
3. 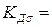 1,57
1,57
4. 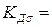 0,78
0,78
8. Чему равен поправочный коэффициент к амплитудному касательному напряжению, если коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали, следующие: 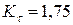 ;
; 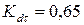 ;
; 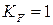 ?
?
1. 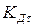 =0,88
=0,88
2. 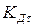 =2,69
=2,69
3. 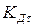 =0,37
=0,37
4. 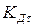 =1,09
=1,09
9. Чему равен коэффициент запаса усталостной прочности по нормальным напряжениям, если 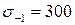 МПа,
МПа, 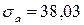 МПа,
МПа, 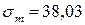 МПа? Коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали, следующие:
МПа? Коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали, следующие: 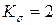 ,
, 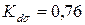 ,
, 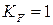 ,
, 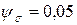 .
.
1. 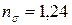
2. 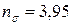
3. 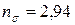
4. 
10. Чему равен коэффициент запаса усталостной прочности по касательным напряжениям, если 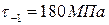 ,
,  ,
, 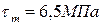 ? Коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали по касательным напряжениям, следующие:
? Коэффициенты, учитывающие влияние конструктивно-технологических факторов на усталостную прочность детали по касательным напряжениям, следующие: 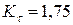 ,
, 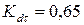 ,
, 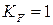 ,
, 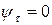 .
.
1. 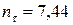
2. 
3. 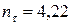
4.