Теоретический материал. Какое нагружение называется динамическим?

Какое нагружение называется динамическим?

Эффект приложения нагрузки в большой степени зависит от скорости её изменения во времени. В связи с этим принято различать статические и динамические нагрузки.

Нагрузка, постоянная или очень медленно изменяющаяся во времени, когда скоростями и ускорениями изменения нагрузки можно пренебречь, называется статической. Расчет на прочность и жесткость при статическом нагружении был изучен в предыдущих разделах дисциплины «Сопротивление материалов».

Нагрузку, быстро изменяющуюся во времени, называют динамической.

К основным видам динамического нагружения относятся следующие: инерционное действие нагрузки (при равноускоренном движении), вибрационное действие нагрузки (при колебательных движениях), ударное действие нагрузки.

Понятно, что изменение напряжения от действия динамического нагружения сильнее, чем от соответствующего статического. Простой пример. Сравним два состояния подмоторной рамы с установленным на ней автомобильным двигателем: когда двигатель выключен и когда он включен. Очевидно, что во втором случае усилия, напряжения и деформации, возникающие в материале рамы, будут гораздо больше, чем в первом.

Как рассчитать на прочность и жесткость конструкцию, испытывающую динамическое действие нагрузки?

Какой бы вид динамического нагружения ни испытывала конструкция, подход к расчету на прочность и жесткость в данном случае единый:

· Данный вид динамической нагрузки заменяют соответствующей статической (прикладывая в той же точке, в том же направлении, но статически) и производят статический расчет на прочность и жесткость.

· Учитывая вид динамического нагружения и используя соответствующие законы физики и теоретической механики, определяют коэффициент динамичности – число, показывающее, во сколько раз значение некоторого динамического фактора (усилия, напряжения или перемещения) больше соответствующего статического значения этого фактора.

· Записывают условие прочности и условие жесткости с учетом статического расчета и найденного коэффициента динамичности:

– условие прочности,

– условие жесткости,

где – коэффициент динамичности, , – максимальные статическое и динамическое напряжения, , – максимальные статическое и динамическое перемещения.

· Условие прочности и условие жесткости решаются в соответствии с поставленной задачей.

В данной теме мы рассмотрим работу элементов упругих конструкций в условиях вынужденных колебаний. Очень часто на конструкции устанавливают различного рода энергоустановки, которые во включенном состоянии совершают колебательные движения, передающиеся на всю конструкцию. Расчет на прочность таких конструкций производится по вышеописанному алгоритму с учетом колебательного движения. Теория колебаний изучается в соответствующем разделе дисциплины «Физика». Что нам нужно знать из теории колебаний?

Что называется числом степеней свободы упругой системы?

Первое, что важно знать при исследовании колебательных движений упругих систем – число степеней свободы, т.е. число независимых переменных, необходимых и достаточных для описания состояния системы в любой момент времени. Проще говоря, число степеней свободы равно числу сосредоточенных масс, расположенных на невесомой упругой системе.

В курсе «Сопротивление материалов» рассматриваются только простейшие упругие системы с одной степенью свободы (с одной сосредоточенной массой).

Как различают механические колебания по причинам, их вызывающим?

Различают следующие типы колебаний:

1. Свободные (собственные) – колебания, возникающие вследствие начального отклонения системы от положения равновесия, и происходящие только под действием сил упругости системы (например, колебания груза, подвешенного на пружине).

2. Вынужденные – колебания, происходящие под действием внешних периодически изменяющихся сил (например, вибрации подмоторной рамы при включенном двигателе).

3. Параметрические – колебания, в процессе которых периодически изменяются параметры системы (например, при вращении несбалансированного автомобильного колеса, при потере устойчивости стержня под действием пульсирующей нагрузки).

4. Автоколебания – колебания, возбуждаемые внешними силами, характер воздействия которых определяется самим колебательным процессом (например, колебания деформируемых тел в потоке жидкости или газа – флаттер).

С прочностной точки зрения наибольший интерес представляют вынужденные колебания, при которых действие периодически изменяющихся сил приводит к возникновению периодически изменяющихся напряжений.

Как различают механические колебания по виду деформации, возникающей в упругой системе в процессе колебаний?

Колебания классифицируют также по виду деформации. Так, для стержней различают продольные (растяжение-сжатие), поперечные (изгиб) и крутильные (кручение)колебания.

Как определить коэффициент динамичности при вынужденных колебаниях упругой системы с одной степенью свободы?

При вынужденных колебаниях коэффициент динамичности принято называть коэффициентом усиления колебаний и обозначать .

Коэффициент динамичности (коэффициент усиления колебаний) при вынужденных колебаниях упругих систем с одной степенью свободы без учета сил сопротивления равен:

, (7.1)

где – частота вынужденных колебаний, определяется параметрами работы энергоустановки; – частота собственных колебаний упругой системы, определяется по формуле:

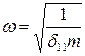. (7.2)

Здесь – масса колеблющегося груза (например, двигателя), – податливость упругой системы, является единичным статическим перемещением сечения, к которому приложена сила веса груза, в направлении колебательного движения. Определяется это единичное перемещение методом Мора.

Что такое явление резонанса?

Если частота вынуждающей силы приближается по значению к частоте собственных колебаний , то, согласно (7.1), коэффициент динамичности . Амплитуда колебаний при этом резко возрастает, а значит, резко возрастает и амплитуда изменения напряжений, что приводит к разрушению конструкции. Это явление называется резонансом.

Алгоритм расчета на прочность при вынужденных колебаниях упругих систем с одной степенью свободы

1. Решение статической задачи.

· Динамическую возмущающую силу заменяем статической, равной её амплитудному значению .

· Строим эпюру ВСФ от действия согласно виду деформации и определяем положение опасного сечения.

· Находим максимальное статическое напряжение .

2. Определение коэффициента динамичности (коэффициента усиления колебаний).

· Находим податливость упругой системы методом Мора.

· Вычисляем частоту собственных колебаний по формуле (7.2).

· Определяем частоту вынужденных колебаний , исходя из условий работы энергоустановки.

· Вычисляем коэффициент динамичности (коэффициент усиления колебаний) по формуле (7.1).

3. Запись условия прочности.

· Если вес колеблющейся массы не участвует в колебательном движении, т.е. направлен перпендикулярно направлению движения, то условие прочности имеет вид:

. (7.3)

· Если направление силы тяжести колеблющейся массы совпадает с направлением колебательного движения, то эта статическая сила также участвует в нагружении упругой системы, но не усиливается коэффициентом динамичности. В этом случае конструкция испытывает комбинированное нагружение – и статическое, и динамическое. Тогда, согласно принципу независимости действия сил, максимальное напряжение, возникающее в конструкции, равно:

.

Учитывая (7.3), получим окончательное выражение для условия прочности:

. (7.4)

4. Решение условия прочности согласно поставленной задаче.

· Найденные значения параметров подставляются в условие прочности (7.3) или (7.4), которое решается согласно поставленной задаче, т.е. производится либо поверочный расчет, либо проектировочный, либо расчет на грузоподъемность.

Дата добавления: 2015-01-29; просмотров: 998 | Нарушение авторских прав | Изречения для студентов

Читайте также:

ПОЧЕМУ ЖЕНЩИНЫ НЕ ОБРАЩАЮТСЯ С ПРОСЬБОЙ

Почему необходим контроль?

Почему трудно полюбить зелень?

Почему мужчины начинают сомневаться

Рекомендуемый контект:

Поиск на сайте:

© 2015-2020 lektsii.org - Контакты - Последнее добавление