Задача
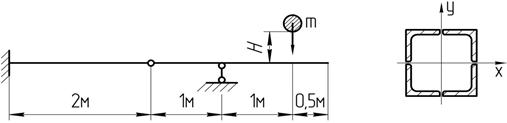
На заданную балку с высоты Н =0,5 м свободно падает абсолютно жесткое тело массой m. Поперечное сечение балки составное – состоит из четырех стальных равнобоких уголков №10, сваренных между собой. Определить допустимую величину массы падающего тела 
, при которой будет обеспечена прочность балки, если 
. Проверить выполнение условия жесткости, приняв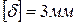 
. Массой балки пренебречь.
Решение
1. Определим геометрические характеристики поперечного сечения балки: осевой момент инерции Ix и осевой момент сопротивления Wx, которые нам потребуются при прочностном и деформационном расчетах.
Поперечное сечение балки сложное – состоит из четырех равнобоких уголков №10:
Оси х и у – главные центральные оси сечения, причем ось у – силовая линия, а ось х – нейтральная линия. По сортаменту (см. Приложение 4, таблица 4.3, стр. 154) для одного равнобокого уголка №10 находим: сторону уголка 
, момент инерции относительно оси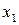 
, площадь 
, расстояние от центра тяжести до стороны уголка 
.
Применяя теорему о суммировании моментов инерции и теорему о параллельном переносе осей (см. Практикум, часть 1, стр. 27-29) найдем осевой момент инерции всего сложного сечения:
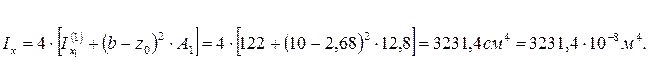
Осевой момент сопротивления Wx находим по определению (см. Практикум, часть 1, стр. 34):
.
2. Решим статическую прочностную часть задачи.
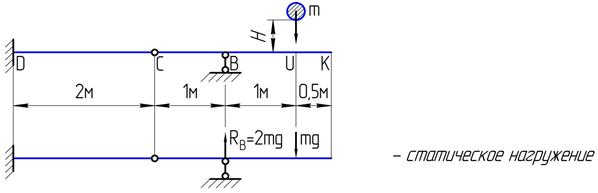
2.1. Приложим к балке в точке удара «U» (в направлении удара) статическую силу, равную весу падающего тела: 
. При этом в подвижной опоре «В» возникает реактивная сила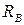 
, которая определяется из моментного уравнения равновесия, записанного относительно врезанного шарнира «С» для правой части балки:
.
2.2. Построим грузовую эпюру изгибающих моментов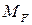 
от действия силы F и определим положение опасного сечения балки. Эпюру строим в направлении от свободного края к жесткой заделке методом сечений с учетом действия силы F и реакции .
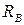Опасное сечение балки – сечение «D», где возникает максимальный момент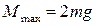 
.
2.3. Определим максимальное статическое напряжение 
в долях массы m. Примем при этом ускорение свободного падения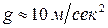 
.
.
3. Определим коэффициент динамичности 
по формуле (8.2). Для этого нам нужно знать податливость упругой системы 
.
3.1. Для определения податливости системы построим единичную эпюру изгибающих моментов 
от действия единичной силы, приложенной в точке удара «U». Очевидно, что эпюра будет отличаться от грузовой эпюры 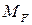лишь тем, что значения моментов в соответствующих сечениях будут в mg раз меньше.
3.2. Определим податливость упругой балки методом Мора, «умножив» единичную эпюру саму на себя. Будем использовать при этом формулу Симпсона. Участков перемножения два: UB и ВD.
.
3.3. Найдем теперь коэффициент динамичности в долях параметра m, используя формулу (8.2).
.
4. Запишем условие прочности при ударе (8.3):
.
5. Подставим в условие прочности значение 
и выражения для и в долях параметра m:
.
Если в неравенстве оставить только знак равенства, то значение параметра массы m будет максимально допустимым . Решим полученное таким образом уравнение относительно .
.
Таким образом, чтобы не нарушилось условие прочности, на балку с высоты Н =0,5 м может упасть тело массой, не более 34,4 кг. Численное значение коэффициента динамичности при этом равно
.
6. Решим статическую деформационную часть задачи.
6.1. Определим, в каком сечении балки возникает максимальный статический прогиб 
. Для этого изобразим приближенный вид изогнутой оси балки, учитывая условия её закрепления и вид грузовой эпюры изгибающих моментов (подробные пояснения – см. тему 1, стр. 16).
Очевидно, что максимальное статическое перемещение возникает в сечении «К».
6.2. Определим методом Мора. Для этого необходимо в сечении «К» приложить единичную безразмерную силу и построить от её действия единичную эпюру изгибающих моментов 
.
«Умножив» единичную эпюру на грузовую 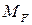, согласно методу Мора, получим искомое перемещение . Применяем при этом простейшую формулу Симпсона. Участков перемножения два: UB и ВD.
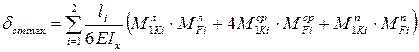. (8.5)
Давайте подумаем 
, как проще можно посчитать эту величину. Выше мы уже отмечали и на рисунке видно, что грузовая эпюра 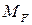пропорциональна единичной эпюре . Коэффициентом пропорциональности является величина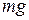 
. Тогда при вычислении по формуле (8.5) грузовую эпюру 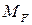можно заменить на единичную эпюру , а коэффициент пропорциональности 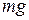вынести за скобку:
.
Таким образом, при статическом нагружении балки максимальное статическое перемещение возникает в сечении «К» и равно 0,27мм.
7. Запишем условие жесткости при ударе и проверим его выполнение.
Условие жесткости при ударе имеет вид (8.4):
.
Подставим в него значение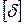 
, найденные значения и и проверим его выполнение.
> ,
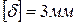следовательно, условие жесткости не выполняется.
Задача решена. 
