 Что такое устойчивость деформируемых упругих систем?
Что такое устойчивость деформируемых упругих систем?
Устойчивостью называется свойство деформируемых упругих систем сохранять заданную форму упругого равновесия под внешним воздействием.
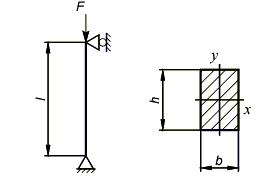
В качестве деформируемой упругой системы мы будем рассматривать центрально сжатую стойку. Например:
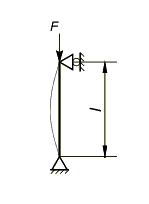
 Что такое критическая сила, критическое напряжение и коэффициент запаса устойчивости?
Что такое критическая сила, критическое напряжение и коэффициент запаса устойчивости?
Величина силы, при которой происходит отклонение от первоначально заданной формы упругого равновесия, называется критической.
Для центрально сжатых стоек – это сила, при которой происходит отклонение от прямолинейной формы вследствие изгиба.
Формула Эйлера для критической силы выведена для случая упругого деформирования, т.е. для напряжений, не превышающих предела пропорциональности 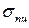 (справочная величина для данного материала стойки).
(справочная величина для данного материала стойки).
Формула Эйлера для критической силы имеет вид:
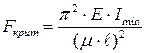
Здесь: 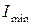 – момент инерции поперечного сечения стойки относительно оси наименьшей жесткости (т.е. оси, относительно которой изогнуть стойку легче); Е – модуль упругости первого рода (модуль Юнга, справочная величина);
– момент инерции поперечного сечения стойки относительно оси наименьшей жесткости (т.е. оси, относительно которой изогнуть стойку легче); Е – модуль упругости первого рода (модуль Юнга, справочная величина); 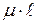 – приведенная длина стойки, равная произведению длины стойки на коэффициент приведения длины (см. ниже).
– приведенная длина стойки, равная произведению длины стойки на коэффициент приведения длины (см. ниже).
Напряжение, возникающее в материале стойки под действием критической силы, называется критическим напряжением.
Формула Эйлера для критического напряжения имеет вид:
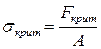 ,
,
где А – площадь поперечного сечения стойки.
Коэффициентом запаса по устойчивости называется число, показывающее, во сколько раз величина критической силы отличается от действующей нагрузки:
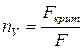 .
.
 Что такое коэффициент приведения длины?
Что такое коэффициент приведения длины?
Коэффициент приведения длины 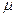 показывает, какую часть длины стойки с данными условиями закрепления занимает одна полуволна синусоиды при потере устойчивости прямолинейной формы. Например:
показывает, какую часть длины стойки с данными условиями закрепления занимает одна полуволна синусоиды при потере устойчивости прямолинейной формы. Например:
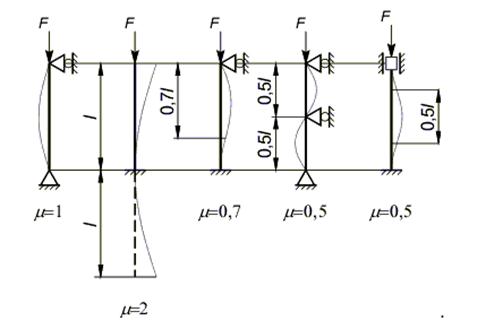
И т.д.
 Что такое гибкость упругой системы?
Что такое гибкость упругой системы?
Гибкостью называется величина, равная
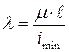 ,
,
где 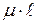 – приведенная длина стойки,
– приведенная длина стойки, 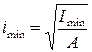 – радиус инерции поперечного сечения относительно оси наименьшей жесткости.
– радиус инерции поперечного сечения относительно оси наименьшей жесткости.
Например, если стойка прямоугольного сечения, то 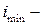 это i у:
это i у:
 Как зависит критическое напряжение от гибкости упругой системы?
Как зависит критическое напряжение от гибкости упругой системы?
Для этого надо знать график зависимости 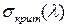 :
:
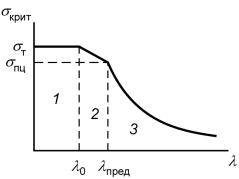
1 – зона малой гибкости;
2 – зона средней гибкости (зона Ясинского);
3 – зона большой гибкости (зона Эйлера).
В области большой гибкости (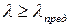 ) критическое напряжение определяется по формуле Эйлера:
) критическое напряжение определяется по формуле Эйлера:
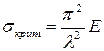 .
.
В области средней гибкости (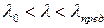 ) критическое напряжение определяется по формуле Ф. Ясинского:
) критическое напряжение определяется по формуле Ф. Ясинского:
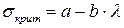 (для сталей).
(для сталей).
Коэффициенты а, b, λ 0и λпред зависят от марки материала и их можно найти в справочных таблицах.
В области малой гибкости (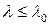 ) расчет на устойчивость производить не имеет смысла, и расчет ведут на прочность при сжатии.
) расчет на устойчивость производить не имеет смысла, и расчет ведут на прочность при сжатии.
 Что такое коэффициент продольного изгиба (коэффициент снижения основного допускаемого напряжения) и как с его использованием проводят расчет на устойчивость?
Что такое коэффициент продольного изгиба (коэффициент снижения основного допускаемого напряжения) и как с его использованием проводят расчет на устойчивость?
Коэффициент продольного изгиба φ – это коэффициент снижения основного допускаемого напряжения материала при сжатии для расчета стержней на устойчивость, т.е.
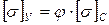 .
.
Коэффициент φ может принимать значения 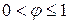 и является табличной функцией, зависящей от гибкости стойки и марки материала. Из условия
и является табличной функцией, зависящей от гибкости стойки и марки материала. Из условия 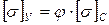 можно получить расчетные формулы для определения размера поперечного сечения заданной формы при известной величине силы F:
можно получить расчетные формулы для определения размера поперечного сечения заданной формы при известной величине силы F:
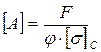
или для определения величины допускаемой нагрузки при известной величине размеров поперечного сечения:
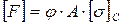 .
.
Алгоритм расчета размеров сечения заданной формы с использованием коэффициента φ (проектировочный расчет), если известны: величина нагрузки, условия закрепления и марка материала 
Данный вид расчета проводится методом последовательных приближений (итерационным методом).
1. Выразить величину площади поперечного сечения А, радиуса инерции относительно оси наименьшей жесткости i min через характерный размер сечения.
2. На первой итерации i=1 задать начальное значение коэффициента продольного изгиба. Обычно берут среднее из интервала его значений, т.е. 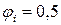 или 0,6.
или 0,6.
3. При первом значении 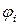 определить значение площади поперечного сечения:
определить значение площади поперечного сечения:
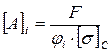 .
.
4. Определить величину характерного размера сечения через полученную площадь и вычислить минимальный радиус инерции.
5. Определить максимальную гибкость стойки:
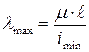 .
.
6. По величине найденной гибкости и марке материала в справочной таблице найти уточненный коэффициент 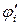 .
.
7. Сравнить 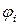 и
и 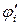 . Если расхождение между коэффициентами существенное (% расхождения > 3%), то необходимо определить их среднеарифметическое значение
. Если расхождение между коэффициентами существенное (% расхождения > 3%), то необходимо определить их среднеарифметическое значение 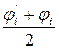 , которое используют на следующей итерации i=i+1, повторяя расчет с пункта №3.
, которое используют на следующей итерации i=i+1, повторяя расчет с пункта №3.
8. Выход из итерационного процесса произвести либо при близком значении 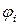 и
и 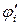 , либо по проценту расхождения между расчетным (действующим) напряжением в конце i-итерации
, либо по проценту расхождения между расчетным (действующим) напряжением в конце i-итерации 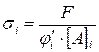 и допускаемым напряжением
и допускаемым напряжением 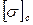 , который не должен превышать 3%:
, который не должен превышать 3%:
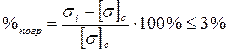 .
.
Алгоритм расчета величины допускаемой нагрузки с использованием коэффициента φ (расчет на грузоподъемность), если известны геометрические размеры стойки, марка материала и способ закрепления 
1. Определить максимальную гибкость стойки по формуле:
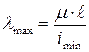 ,
,
предварительно вычислив значение радиуса инерции с использованием формулы:
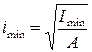
или, если сечение представляет собой прокатный профиль, взяв его значение из таблиц сортамента.
2. По таблице коэффициента  в соответствии с маркой материала и величиной гибкости выписать значение коэффициента.
в соответствии с маркой материала и величиной гибкости выписать значение коэффициента.
3. Применить формулу 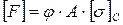 .
.
4. Выписать из справочной таблицы (если нет в условии задачи) значения  и
и 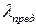 и путем сравнения расчетной величины
и путем сравнения расчетной величины 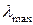 c
c  и
и 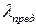 определить, к какой зоне графика
определить, к какой зоне графика 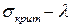 относится данная стойка.
относится данная стойка.
5. Если 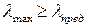 , величину критической силы определяем по формуле Эйлера:
, величину критической силы определяем по формуле Эйлера:
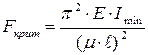 .
.
6. Если  <
< 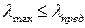 , то величину критической силы рассчитываем по формуле Ясинского:
, то величину критической силы рассчитываем по формуле Ясинского:
 ,
,
для которой коэффициенты a и b берем из справочных таблиц в соответствие с маркой материала.
7. Если 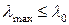 , то значение критической силы принимает смысл значения силы, при которой начинаются массовые пластические деформации, т.е.
, то значение критической силы принимает смысл значения силы, при которой начинаются массовые пластические деформации, т.е. 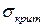 достигает уровня предела текучести
достигает уровня предела текучести 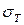 , а
, а 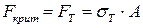 .
.






