Пример решения задачи. Консольная рама из двух элементов одинаковой длины (l = 2 м) нагружена пространственной системой сил

Консольная рама из двух элементов одинаковой длины (l = 2 м) нагружена пространственной системой сил. Материал рамы – сталь марки Ст3 с допускаемым напряжением [s] = 160 МПа.

Требуется подобрать для рамы из условия прочности размеры двух видов поперечного сечения: круглого с диаметром d и прямоугольного с соотношением длин сторон h / b = 2. Определить, какое сечение является более эффективным с точки зрения расхода материала.

Решение

1. Построим эпюры продольной силы N, изгибающих M_x, M_y и крутящих моментов M_z.

Введем для каждого стержня систему координат. При этом ось z всегда направляется вдоль оси стержня, а оси x и y являются главными центральными осями поперечного сечения.

В качестве базы для построения эпюр используем конфигурацию рамы, которую вычерчиваем в любом удобном месте.

Элемент I (AB)

Продольная сила.

В начале элемента (сечение A) нет силы, действующей вдоль оси z, поэтому N = 0.

Изгибающий момент в плоскости yz.

В этой плоскости на элемент I действуют сосредоточенная сила F ₁ и равномерно распределенная нагрузка q. Наличие распределенной нагрузки говорит о том, что эпюра изгибающих моментов M_x должна иметь вид параболы с выпуклостью, направленной вниз (в сторону действия нагрузки q). Строим эту параболу по двум точкам.

В начале элемента отсутствует сосредоточенный внешний момент, поэтому .

Вычисляем величину изгибающего момента в конце элемента:

(растянуты нижние волокна).

Изгибающий момент в плоскости xz.

В этой плоскости на элемент I действует сосредоточенная сила F ₂. Так как распределенной нагрузки нет, эпюра изгибающих моментов M_y должна быть прямолинейной. Строим эту прямую по двум точкам.

В начале элемента отсутствует сосредоточенный внешний момент, поэтому .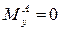

Вычисляем величину изгибающего момента в конце элемента:

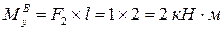(растянуты задние волокна).

Крутящий момент.

На элемент I не действуют моменты относительно оси z, поэтому M_z = 0.

Элемент II (BC)

Отсечем и отбросим элемент I рамы. К оставшемуся элементу II в сечении B прикладываем силы, перенося их с элемента I (при этом распределенная нагрузка заменяется равнодействующей силой ). Кроме того, в сечении B прикладываем моменты, полученные в конце элемента I. Их величину и направление устанавливаем по эпюрам M_x и M_y. Моменты действуют в той же плоскости, в которой находится соответствующая эпюра, а их направление будет навстречу движению вдоль линии эпюры:

Получаем следующую расчетную схему для элемента II:

Продольная сила.

Действующая вдоль оси z сила F ₂ растягивает элемент II, поэтому возникающая продольная сила положительна и равна по величине N = F ₂ = 1 кН. На эпюре изображаем прямоугольник с ординатой 1 кН, откладывая ее от базы в любом направлении. В поле эпюры указываем знак «+».

Изгибающий момент в плоскости yz.

В данной плоскости на элемент II действуют сосредоточенные силы F ₁ и Q. По отсутствию распределенной нагрузки определяем, что эпюра M _x должна быть прямолинейной.

В начале элемента в данной плоскости нет сосредоточенного момента, поэтому .

В конце элемента:

(растянуты нижние волокна).

Изгибающий момент в плоскости xz.

В этой плоскости на элемент II действует сосредоточенный момент 2 кН · м и сила F ₃. Распределенная нагрузка отсутствует, поэтому эпюра M _y имеет вид прямой линии.

В начале элемента действует момент 2 кН · м, растягивающий левые волокна, то есть .

В конце элемента:

(растянуты левые волокна).

Крутящий момент.

Действующий по часовой стрелке относительно оси z момент 4 кН · м приводит к возникновению в поперечных сечениях элемента II крутящего момента M_z = 4 кН · м.

В окончательном виде эпюры внутренних силовых факторов выглядят следующим образом:

2. Определение размеров круглого сечения.

По эпюрам внутренних силовых факторов видно, что элемент II является более нагруженным по сравнению с элементом I: здесь больше величины изгибающих моментов M _x и M _y и, кроме того, имеются крутящий момент M _z и продольная сила N. Поэтому для выполнения проектного расчета выбираем элемент II.

2.1. Расчет на прочность для элемента II (BC)

2.1.1. Определяем положение опасного сечения.

Из эпюр изгибающих моментов видно, что для элемента II наибольшие значения моментов M_x (2 кН·м) и M_y (6 кН·м) возникают в одном и том же сечении – сечении C. Оно и является опасным.

2.1.2. Определяем положение опасной точки в опасном сечении.

Сначала найдем положение силовой линии в опасном сечении. Для этого изобразим сечение и от его центра отложим ординаты изгибающих моментов M_x и M_y с соблюдением масштаба и в ту же сторону, что и на эпюрах. Геометрическая сумма ординат M_x и M_y дает ординату суммарного изгибающего момента M _Σ, которая и определяет положение силовой линии.

Опасными от действия изгиба будут точки пересечения силовой линии с контуром круга a и c. То, что ордината M _Σ отложена в сторону точки а, означает, что эта точка испытывает напряжение растяжения. Ставим рядом с ней знак «+». Противоположная ей точка с испытывает напряжение сжатия, и рядом с ней ставим знак «–».

Добавим около каждой точки по знаку «+» от действия растягивающей продольной силы N. В точке a получаем два знака «+», исходя из чего делаем вывод, что эта точка опаснее, чем точка c.

Поскольку возникающие от крутящего момента M_z касательные напряжения τ в точках a и c одинаковы, именно точка a и является опасной при совместном действии изгиба с растяжением и кручением.

2.1.3. Составляем и решаем условие прочности для опасной точки.

По теореме Пифагора вычисляем величину суммарного изгибающего момента:

.

Определяем напряжения в опасной точке, пренебрегая влиянием продольной силы N:

;

.

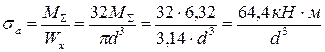Чтобы оценить степень опасности состояния материала в точке a, вычисляем эквивалентное напряжение. Так как сталь Ст3 является пластичным материалом, то следует выбрать III или IV теорию предельного состояния. Воспользуемся более точной IV теорией:

.

Из условия прочности: 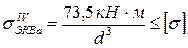– выражаем и вычисляем минимально необходимое значение диаметра сечения:

.

Выполним проверку на прочность для опасной точки с учетом продольной силы N:

,

,

.

Это больше, чем допускаемое напряжение [ s ] = 160 МПа. Перегруз составляет , что не превышает 5%. Такой перегруз считается допустимым, и увеличивать диаметр сечения нет необходимости.

2.2. Проверка на прочность для элемента I (AB)

Проверим, можно ли использовать для элемента I сечение, подобранное для элемента II.

2.2.1. Из эпюр внутренних силовых факторов видно, что опасным для элемента I является сечение B, испытывающее прямой пространственный изгиб.

2.2.2. В плоскости круглого сечения откладываем ординаты изгибающих моментов M _x и M _y для сечения B по тем же направлениям, что и на эпюре. Вдоль ординаты суммарного момента проводим силовую линию. Так как для элемента I продольная сила N отсутствует, опасными являются точки пересечения силовой линии с контуром сечения j и k.

2.2.3. Вычисляем величину напряжения в опасных точках:

.

Это меньше, чем допускаемое напряжение, так что увеличивать размеры сечения не нужно.

3. Определение размеров прямоугольного сечения.

Определим предварительно рациональное расположение сечения и его геометрические характеристики.

Наибольший изгибающий момент для рамы в целом возникает на элементе II (6 кН·м). Ордината этого момента отложена на эпюре вдоль оси x элемента II, поэтому выгодно расположить прямоугольное сечение таким образом, чтобы его длинные стороны были параллельны этой оси (большей стороной вдоль большего изгибающего момента).

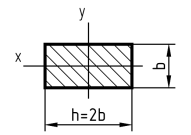
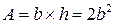Выразим геометрические характеристики сечения через его характерный размер b. Так как , то площадь сечения , а осевые моменты сопротивления для выбранного расположения сечения:

;

.

По таблице 4.5 Приложения 4 (стр. 157) определяем значения коэффициентов b и g для отношения h / b = 2:

b = 0,493, g = 0,795.

Момент сопротивления сечения при кручении .

Так же, как и в случае круглого сечения, сначала подбираем размеры сечения для элемента II, а затем проверяем, подходит ли это сечение для элемента I.

3.1. Расчет на прочность для элемента II (BC)

3.1.1. Определяем положение опасного сечения.

Так же, как и в случае стержня круглого сечения, опасным является сечение C, поскольку здесь максимальны значения изгибающих моментов M_x и M_y.

3.1.2. Определяем положение опасных точек в опасном сечении.

Найдем опасные точки от действия изгиба. Для этого в плоскости сечения отложим ординаты внутренних изгибающих моментов M_x и M_y и установим положение силовой линии. Силовая линия совпадает с ординатой суммарного момента M _Σ. Опасными от изгиба будут вершины прямоугольника e и f, находящиеся в тех четвертях, через которые проходит силовая линия.

По положению ординаты суммарного изгибающего момента определяем, что в точке f возникает напряжение растяжения, ставим рядом с ней два знака «+». Точка e испытывает напряжение сжатия, и около неё ставим два знака «–». Добавив к каждой группе знаков знак «+» от действия растягивающей продольной силы N, видим, что более опасной является точка f.

Проставим также векторы касательных напряжений в точках по серединам сторон прямоугольника. Они направлены вдоль контура сечения по часовой стрелке относительно его центра (так же, как и крутящий момент M_z). Из этих четырех точек выберем для расчета две, находящиеся в той же четверти, что и точка f (точки m и n).

Опасной является одна из трех точек: f, m или n.

3.1.3. Составляем и решаем условие прочности.

Найдем расчетные напряжения в опасных точках, пренебрегая влиянием продольной силы N.

В угловой точке f:

, .

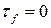Точка n лежит на оси y, поэтому нормальное напряжение в ней возникает только от действия момента M_x:

.

Касательное напряжение в точке n является максимальным, так как она находится посередине длинной стороны сечения:

.

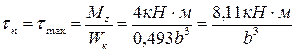Эквивалентное напряжение для точки n (по IV теории предельного состояния):

.

В точке m нормальное напряжение определяется только моментом M_y (поскольку она лежит на оси x), а касательное напряжение равно произведению τ _max на коэффициент g (в силу того, что эта точка находится посередине короткой стороны сечения):

, .

Эквивалентное напряжение для точки m:

.

В условие прочности подставляем большее из рассчитанных напряжений:

,

откуда находим минимально необходимые размеры сечения:

,

.

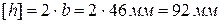Опасной является точка с максимальным расчетным напряжением – точка n. Выполняем для нее проверку на прочность с учетом продольной силы N.

,

,

.

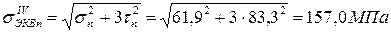Полученное значение меньше допускаемого напряжения [ s ] = 160 МПа, так что условие прочности выполняется.

3.2. Проверка на прочность для элемента I (AB)

3.2.1. Для данного элемента опасным является сечение B. Вид деформации – косой изгиб.

3.2.2. Изображаем схему сечения. От его центра тяжести откладываем в масштабе ординаты изгибающих моментов M _x и M _y в тех же направлениях, что и на эпюре для сечения B. Геометрическая сумма этих ординат дает ординату суммарного изгибающего момента, продлевая которую получим силовую линию. Так как продольная сила N для элемента I отсутствует, опасными являются угловые точки в четвертях, через которые проходит силовая линия. Это точки u и v.

3.2.3. Вычисляем величину напряжения в опасных точках:

.

Это меньше, чем допускаемое напряжение [ s ] = 160 МПа, то есть условие прочности выполняется.

4. Сравним стержни круглого и прямоугольного сечения по металлозатратам. Для этого определим площади сечений:

,

,

то есть в данном случае прямоугольное сечение, обладая меньшей площадью, является более эффективным с точки зрения расхода материала.

Задача решена.

 

Что делать, если условие прочности в пункте
2.2.3 или 3.2.3 не выполняется?

В этом случае размеры сечения (d или b и h) нужно увеличить в 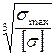раз и повторить проверку.