Прямоугольное поперечное сечение

При кручении стержня прямоугольного сечения касательное напряжение неодинаково в разных точках его контура. Оно достигает максимальных значений по серединам сторон сечения и равно нулю в вершинах. Поэтому при расчете на прочность в случае изгиба с кручением и растяжением-сжатием стержней прямоугольного сечения рассматривают в качестве возможных опасных три точки:

а) угловая точка, в которой возникают нормальные напряжения одного знака от изгиба и растяжения-сжатия, а касательные напряжения равны нулю:

; (4.2)

б) две точки по серединам длин сторон прямоугольника в той же четверти, что и опасная угловая. Нормальные напряжения в этих точках определяются по формулам:

– в точке на оси x; (4.3)

– в точке на оси y. (4.4)

Касательные напряжения:

– посередине длинной стороны; (4.5)

– посередине короткой стороны. (4.6)

В последних двух формулах момент сопротивления кручению , где b – длина короткой стороны сечения, а β и γ – коэффициенты, зависящие от соотношения длин сторон прямоугольника (см. Приложение 4, таблица 4.5, стр. 157).

Как быть, если поперечное сечение прямоугольное,
а изгиб возникает только в одной плоскости (прямой изгиб)?

В данном случае – при сочетании прямого изгиба с растяжением-сжатием и кручением – потенциально опасными являются две точки:

а) точка на пересечении силовой линии с контуром сечения, с той стороны, где нормальные напряжения от изгиба и от растяжения-сжатия одного знака;

б) две равноопасных точки, лежащих посередине сторон, параллельных силовой линии.

Напряжения в этих точках определяются по формулам (4.3–4.6).

Как записать условие прочности для точки, в которой
возникает и нормальное, и касательное напряжение?

Если в какой-либо точке поперечного сечения стержня одновременно возникают как нормальные, так и касательные напряжения, то это является признаком того, что данная точка находится в плоском напряженном состоянии.

Для расчета на прочность в условиях плоского напряженного состояния используются теории предельного состояния, также называемые теориями или гипотезами прочности.

Теории предельного состояния высказывают предположения (гипотезы) об условиях перехода материала конструкции в предельное состояние, при котором конструкция теряет несущую способность. Рассматривается два вида предельных состояний: хрупкое разрушение и возникновение чрезмерных необратимых (пластических) деформаций. Так как механизмы этих двух процессов различаются, единой теории предельного состояния, применимой для всех материалов, быть не может.

Любая теория предельного состояния позволяет заменить сложное напряженное состояние эквивалентным ему по степени опасности одноосным растяжением. Нормальное напряжение σ _экв, соответствующее такому одноосному растяжению, называется эквивалентным напряжением. Это дает возможность составить условие прочности в виде:

,

где σ и τ – нормальное и касательное напряжение в исследуемой точке поперечного сечения стержня, f (σ, τ) – некоторая функция σ и τ, задаваемая теорией предельного состояния, [ σ ]_р – допускаемое напряжение материала при одноосном растяжении.

Какие теории предельного состояния используются для пластичных материалов и как при этом найти эквивалентное напряжение?

Для расчета на прочность стержней из пластичных материалов считаются одинаково приемлемыми III и IV теории прочности, однако IV теория лучше согласуется с экспериментальными данными.

Эквивалентное напряжение по III теории прочности (теории наибольших касательных напряжений) вычисляется по формуле:

(4.7)

Эквивалентное напряжение по IV (энергетической) теории прочности вычисляется по следующей формуле:

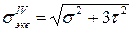(4.8)

 

Алгоритм расчета на прочность при изгибе
с кручением и растяжением-сжатием

1. Определение положения опасного сечения на элементе конструкции по эпюрам изгибающих моментов.

2. Определение положения опасных точек в опасном сечении. Для этого сначала нужно найти положение опасной точки только от действия изгиба с растяжением-сжатием (см. тему 3, алгоритм расчета на прочность, пункт 2, стр.30).

· В случае круглого сечения именно эта точка является опасной и при добавлении кручения.

· В случае прямоугольного сечения наряду с угловой опасной точкой необходимо рассмотреть также еще две точки, расположенные по серединам длин сторон прямоугольника в той же четверти, что и найденная угловая точка. В каждой из трех точек нужно посчитать расчетные напряжения по соответствующим формулам (4.2) – (4.8). Наиболее опасной из трех точек будет та, в которой наибольшее расчетное напряжение.

3. Запись условия прочности для опасной точки и его решение согласно поставленной задаче.

В условии прочности наибольшее расчетное напряжение, возникающее в опасной точке опасного сечения, сравнивается с допускаемым напряжением:

Полученное неравенство решается согласно поставленной задаче.

Если выполняется проектный расчет, то напряжением от продольной силы N на первом этапе пренебрегают. После определения размеров сечения выполняют проверку на прочность для опасной точки с учетом продольной силы. Если перенапряжение не превышает 5% от величины допускаемого напряжения, то принимают подобранные размеры. Если это условие не выполняется, то размеры сечения увеличивают и повторяют проверку.