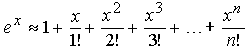Точка перегиба функции это точка,в которой существует касательная к графику и существует такая окрестность точки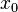 
, в которой график имеет разные направления выпуклости.
Необходимые условия наличия перегиба
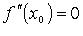либо 
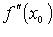не существует.
Достаточные условия наличия перегиба
1. Если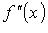 
меняет знак при переходе через точку x0, то x0 - точка перегиба.
2. Если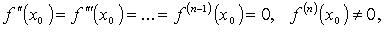 
то при n четном x0 - точка перегиба, при n нечетном x0 не является точкой перегиба.
22. Понятие о многочлене Тейлора. Формула Тейлора для функции одной переменной (без доказательства). Формула Маклорена для функций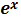 
, 
, 
.
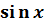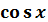Рассмотрим многочлен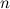 
-й степени
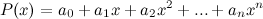
Его можно представить в виде суммы степеней 
, взятых с некоторыми коэффициентами. Продифференцируем его 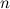раз по переменной , а затем найдем значения многочлена и его производных в точке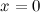 
:
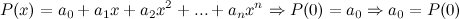
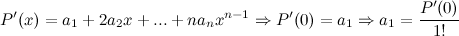
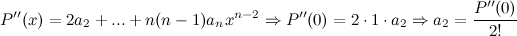
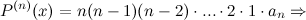
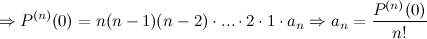
Таким образом, получаем, что
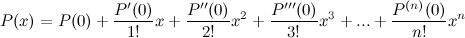
Полученное выражение называется формулой Маклорена для многочлена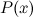 
степени .
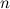Рассуждая аналогично, можно разложить многочлен 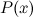по степеням разности 
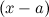, где 
- любое число. В этом случае будем иметь:
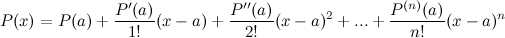
Это выражение называется формулой Тейлора для многочлена 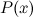в окрестности точки .
Разложение функции ex
Так как (ex)' = ex, то производная любого порядка функции ex равна ex. При x = 0 функция ex и ее производные любого порядка равны одному. Таким образом, формула Маклорена для функции ex имеет вид
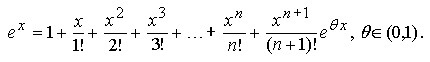
Отметим, что для любого вещественного числа x остаточный член
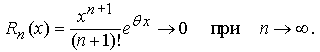
В самом деле, если x – фиксированное число, то, начиная с некоторого положительного целого числа N, для любого n > N имеем
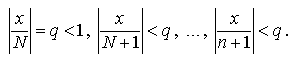
Следовательно
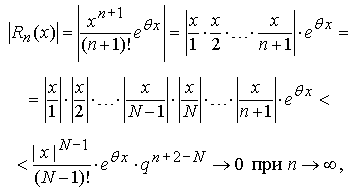
так как q < 1, а величина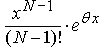 
является постоянной при любом n. Таким образом, значения функции ex могут быть найдены приближенно по формуле:
