1) Определение. Производной функции 
называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
.
2) Геометрическая интерпретация
Обратимся к рисунку 1, на котором представлен фрагмент графика функции 
.
Рис. 1. Секущая AB образует угол β с положительным направлением оси 0 x. Касательная к графику функции проведена в точке A.
Угловой коэффициент секущей AB равен средней скорости изменения функции 
на промежутке [ x, x + ∆ x ]:
| (5) |
Предельным положением секущей AB при перемещении точки B к точке A по дуге кривой является касательная к графику в точке A. Поэтому угловой коэффициент касательной равен пределу углового коэффициента секущей при ∆ x → 0:
| (6) |
Рис. 2. Касательная является предельным положением секущей AB при перемещении точки B к точке A.
Таким образом, производная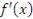 
в точке x равна тангенсу угла, образованного касательной к графику функции в этой точке с положительным направлением оси 0 x.
Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x (t) времени t. В течение интервала времени от t 0 до t 0 + 
точка перемещается на расстояние: x (t 0 + ) - x (t 0) = 
, а её средняя скорость равна: va = / . При 
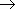0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t 0) материальной точки в момент времени t 0. Но по определению производной мы имеем:
отсюда, v (t 0) = x’ (t 0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ (t).
