Направление выпуклости графика функции.
Опр. 1. График функции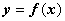 
имеет на интервале 
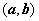выпуклость, направленную вниз, если он расположен не ниже любой касательной, проведённой на этом интервале.
Опр.2. График функции 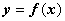имеет на интервале 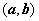выпуклость, направленную вверх, если он расположен не выше любой касательной, проведённой на этом интервале.
Теор.1. (Достаточное условие выпуклости графика функции). Если функция 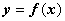имеет на интервале 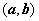вторую производную, и 
(
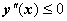) для 
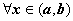, то её график имеет на этом интервале выпуклость, направленную вниз (вверх).
Док-во. Пусть, для определённости, на 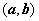. Пусть с - произвольная точка 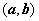, докажем, что график функции лежит выше касательной, проведённой к нему в точке 
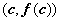. Уравнение касательной: 
(
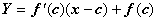- текущая точка касательной).
По формуле Тейлора 
. Вычитая из этого равенства предыдущее, получим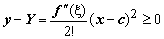 
на 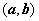, т.е. точка графика функции действительно лежит выше точки графика касательной.
Аналогично рассматривается случай 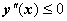на .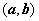
