При разложении периодического сигнала 
в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут:
(1.10)
или
(1.11)
Интервал ортогональности в обоих случаях совпадает с периодом
функции .
Система функций (1.10) приводит к тригонометрической форме ряда Фурье, а система (1.11)- к комплексной форме.
Ряд Фурье можно записать в форме (используем выражение (1.11):
(1.12)
Совокупность коэффициентов 
ряда Фурье в базисе тригонометрических функций называется частотным спектром периодического сигнала. Коэффициенты ряда (1.12) 
легко определяются с помощью формул (1.9).
Норма базиса:
(1.13)
Таким образом независимо от 
.
Используя (1.9) получаем:
(1.14)
В выражениях (1.13) и (1.14) учтем, что функции 
соответствует комплексно-сопряженная функция 
Коэффициенты в общем случае являются комплексными величинами. Подставив в (1.14) 
получим:
(1.15)
Косинусная (действительная) и синусная (мнимая) части коэффициента определяются формулами:
(1.16)
Коэффициенты часто бывает удобно записать в форме
(1.17)
где
(1.18)
Общее выражение (1.12) можно привести к виду
(1.19)
Перейдем к тригонометрической форме ряда Фурье:
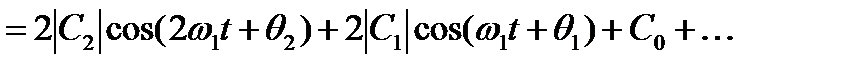
(1.20)
Отсюда видно, что при переходе к тригонометрической форме ряд (1.19) необходимо записать следующим образом:
(1.21)
Вместо выражения (1.21) часто встречается следующая форма записи:
(1.22)
причем 
Из сопоставления выражений (1.22) и (1.21) видно, что амплитуда 
-й гармоники 
связана с коэффициентом ряда (1.19) соотношением 
а 
Таким образом, для всех положительных значений (включая и 
)
(1.23)
Две характеристики - амплитудная и фазовая, т.е. модули и аргументы комплексных коэффициентов ряда Фурье, полностью определяют структуру частотного спектра периодического колебания.
Спектр периодической функции называется линейчатым или дискретным, т.к. состоит из отдельных линий, соответствующих дискретным частотам 
и т.д.
рис.1.2
Использование для гармонического анализа сложных периодических колебаний рядов Фурье в сочетании с принципом наполнения представляет собой эффективное средство для изучения влияния линейных цепей на прохождение сигналов.
