Определение. Подмножество 
элементов группы 
называется подгруппой, если оно само образует группу относительно действия в .
Из этого определения следует, что если 
, то и 
. Очевидно, что единица является единицей . Действительно, если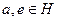 
, то 
и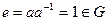 
. Таким образом, единица группы принадлежит любой ее подгруппе. В силу единственности обратного элемента в группе следует, что обратный элемент для любого элемента подгруппы будет для него обратным и во всей группе.
Теорема. Если подмножество элементов группы содержит вместе с двумя элементами 
их произведение 
и вместе с каждым элементом 
его обратный элемент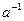 
, то есть подгруппа .
Доказательство. Для того чтобы множество было подгруппой, достаточно показать, что оно обладает единицей. Но в группе 
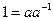при 
. Подмножество вместе с каждым элементом содержит его обратный элемент 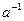и их произведение. Следовательно, оно содержит и единицу. Теорема доказана.