Одной из главных задач арифметики остатков является решение уравнения 
относительно 
. Линейное уравнение 
с вещественными коэффициентами при 
всегда разрешимо. Если же рассматривать его над кольцом целых чисел, то такое уравнение может не иметь решения. Рассмотрим некоторые уравнения в кольце вычетов.
Уравнение 
имеет ровно одно решение. Действительно, 
, где 
, или 
. Тогда 
. Это возможно только в случае, если 
. Однако, в этом случае 
и 
при любом 
, т. е. все решения этого уравнения равны между собой по модулю 143. Рассмотрим уравнение 
. В этом случае 
, где , или 
, т. е. уравнение не имеет решений. Уравнение 
(
) имеет 11 решений (при 
, т. к. - целое число, причем 
).
Таким образом, встает вопрос, при каких значениях 
и 
уравнение имеет решения и как их все найти.
Существует критерий, позволяющий определить, имеет ли данное уравнение ни одного, одно или несколько решение.
1. Если НОД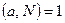 
, то существует равно одно решение. Оно может быть найдено с помощью промежуточного числа 
, удовлетворяющего уравнению 
, после чего искомое неизвестное вычисляется по формуле 
.
Пример. Рассмотрим уравнение . В этом случае НОД 
и можно взять 
. Тогда 
. Если взять 
, то 
. В общем виде можно взять 
и 
.
2. Если НОД 
и 
НОД 
делит 
, то уравнение будет иметь 
решений. Чтобы их найти, нужно разделить исходное уравнение на : 
, где 
, 
, 
. Если 
- решение полученного уравнения, то решение исходного - любое число вида 
, где 
.
Пример. Рассмотрим уравнение . В этом случае НОД 
и уравнение имеет 11 решений. Тогда 
. Решение полученного уравнения 
и 
, 
.
3. В других случаях решений нет.
Определение. Числа 
и называются взаимно простыми, если НОД .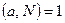
Число элементов кольца 
, взаимно простых с , дается функцией Эйлера 
и равно 
. Значение можно найти по разложению числа на простые множители. Если 
, где 
- различные простые числа, то 
.
По разложению числа на простые множители очень легко вычислить . Особый интерес представляют следующие случаи:
1. Если - простое, то 
.
2. Если и 
- простые числа и 
, то 
.
