Множество остатков  с операциями сложения и умножения является коммутативным кольцом, которое часто называется кольцом вычетов по модулю
с операциями сложения и умножения является коммутативным кольцом, которое часто называется кольцом вычетов по модулю  .
.
Все возможные остатки от деления чисел на  образуют множество
образуют множество  . Очевидно, что
. Очевидно, что  - множество значений оператора модуля
- множество значений оператора модуля  . Некоторые авторы обозначают это множество
. Некоторые авторы обозначают это множество  . Обозначим множество обратимых элементов в
. Обозначим множество обратимых элементов в 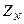 как
как 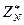 , т. е.
, т. е. 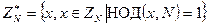 .
.
Поле – это коммутативное кольцо, в котором каждый ненулевой элемент обратим.
Множество 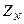 является конечным полем, которое обычно называется полем вычетов по модулю
является конечным полем, которое обычно называется полем вычетов по модулю  и обозначается символом
и обозначается символом 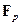 . Из определения следует, что мультипликативная группа
. Из определения следует, что мультипликативная группа 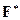 поля
поля 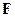 совпадает с множеством
совпадает с множеством 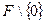 . В частном случае поля вычетов получаем
. В частном случае поля вычетов получаем 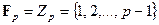 и
и 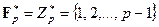 .
.
Закрепим букву  за простым числом и рассмотрим множество многочленов от переменной
за простым числом и рассмотрим множество многочленов от переменной  с коэффициентами из
с коэффициентами из 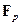 . Это множество обозначается
. Это множество обозначается 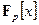 и образует кольцо относительно естественных операций суммы и умножения многочленов.
и образует кольцо относительно естественных операций суммы и умножения многочленов.
Особый интерес представляет случай 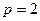 . Например, в кольце
. Например, в кольце 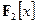 выполнены равенства
выполнены равенства 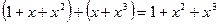 и
и 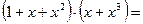
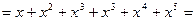
 .
.
Можно зафиксировать многочлен 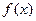 и рассматривать остальные элементы кольца
и рассматривать остальные элементы кольца 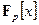 по модулю
по модулю 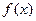 , т. е. оперировать с остатками от деления многочленов на
, т. е. оперировать с остатками от деления многочленов на 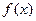 . Как и натуральные числа по модулю
. Как и натуральные числа по модулю  , возможные остатки будут образовывать кольцо. Оно обозначается
, возможные остатки будут образовывать кольцо. Оно обозначается 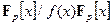 или
или 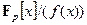 .
.
Пример. Пусть 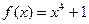 и
и 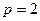 . Тогда
. Тогда 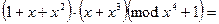
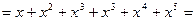
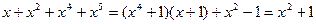 , так кА все коэффициенты рассматриваются по модулю 2.
, так кА все коэффициенты рассматриваются по модулю 2.
При знакомстве с целыми числами по модулю  нас интересовало уравнение
нас интересовало уравнение  . Можно поставить аналогичный вопрос и для многочленов.
. Можно поставить аналогичный вопрос и для многочленов.
Пусть 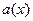 ,
, 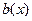 ,
, 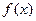 - многочлены из
- многочлены из 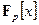 . Существует ли решение уравнения
. Существует ли решение уравнения 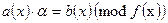 . Относительно
. Относительно 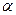 ? Ответ здесь, как и для чисел по модулю
? Ответ здесь, как и для чисел по модулю  зависит от наибольшего общего делителя многочленов
зависит от наибольшего общего делителя многочленов 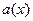 и
и 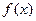 . Возможны три случая. Самым интересным является случай, когда
. Возможны три случая. Самым интересным является случай, когда 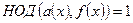 , т. е. многочлены
, т. е. многочлены 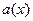 и
и 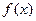 взаимно простые.
взаимно простые.
Определение. Многочлен называется неприводимым, если у него нет делителей, отличных от него самого и констант.
Таким образом, неприводимость многочленов - то же самое, что и простота целых чисел. Вспомним, что целые числа по модулю  образуют поле, только если
образуют поле, только если  - простое число. Аналогично кольцо
- простое число. Аналогично кольцо 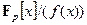 является конечным полем тогда и только тогда, когда многочлен
является конечным полем тогда и только тогда, когда многочлен 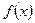 неприводим.
неприводим.
Предположим, что 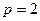 и рассмотрим два неприводимых многочлена
и рассмотрим два неприводимых многочлена 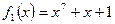 и
и 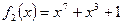 . Возникают два конечных поля
. Возникают два конечных поля 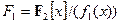 и
и 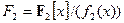 , каждое из которых состоит из 27 двоичных многочленов (любой такой многочлен имеет ровно 7 коэффициентов, равных 0 или 1, поэтому всех многочленов будет 27), степень которых не превосходит 6. Сложение в обоих полях выглядит одинаково, т. к. при вычислении суммы складываются коэффициенты по модулю 2. А вот умножаются элементы этих полей по-разному:
, каждое из которых состоит из 27 двоичных многочленов (любой такой многочлен имеет ровно 7 коэффициентов, равных 0 или 1, поэтому всех многочленов будет 27), степень которых не превосходит 6. Сложение в обоих полях выглядит одинаково, т. к. при вычислении суммы складываются коэффициенты по модулю 2. А вот умножаются элементы этих полей по-разному: 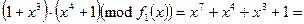
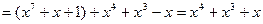 и
и 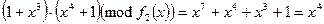 .
.
Будут ли поля 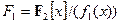 и
и 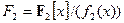 действительно различны или это различие кажущееся?
действительно различны или это различие кажущееся?
Определение. Поля 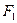 и
и 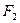 называются изоморфными, если существует отображение
называются изоморфными, если существует отображение 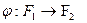 , называемое изоморфизмом, которое удовлетворяет условиям:
, называемое изоморфизмом, которое удовлетворяет условиям: 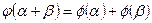 и
и 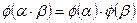 .
.
Изоморфизм существует между любыми двумя конечными полями с одинаковым числом элементов. В частности, он существует и между полями 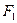 и
и 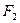 .
.
Приведенные выше конструкции по существу одинаковы и дают единственный способ построения конечных полей. Следовательно, все конечные поля фактически совпадают либо с целыми числами по простому модулю, либо с многочленами по модулю неприводимого многочлена (который тоже можно назвать простым). Также имеет место равенство 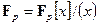 . Поэтому можно утверждать единственность конструкции конечных полей. Таким образом, приходим к фундаментальной теореме о конечных полях.
. Поэтому можно утверждать единственность конструкции конечных полей. Таким образом, приходим к фундаментальной теореме о конечных полях.
Теорема. Существует единственное (с точностью до изоморфизма) конечное поле с числом элементов, равным степени простого числа.
Обозначим поле из 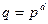 элементов символом
элементов символом 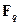 или
или 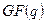 (поле Галуа из
(поле Галуа из  элементов). Так иногда называют конечные поля
элементов). Так иногда называют конечные поля
Любое конечное поле  содержит в себе поле целых чисел по некоторому простому модулю
содержит в себе поле целых чисел по некоторому простому модулю  . Это поле называется простым подполем поля
. Это поле называется простым подполем поля  . Число
. Число  элементов простого подполя называется характеристикой поля и обозначается
элементов простого подполя называется характеристикой поля и обозначается 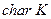 . В частности,
. В частности, 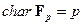 .
.
На конечном поле характеристики  можно определить так называемое отображение Фробениуса:
можно определить так называемое отображение Фробениуса: 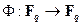 ,
, 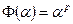 . Отображение Фробениуса является изоморфизмом поля
. Отображение Фробениуса является изоморфизмом поля 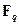 с самим собой. Такие изоморфизмы называется автоморфизмами. Отображение Фробениуса замечательно тем, что множество элементов из
с самим собой. Такие изоморфизмы называется автоморфизмами. Отображение Фробениуса замечательно тем, что множество элементов из 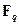 , остающихся неподвижными при отображении
, остающихся неподвижными при отображении 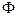 , совпадает с его простым подполем, т. е.
, совпадает с его простым подполем, т. е. 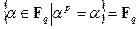 .
.
Если 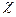 - произвольный автоморфизм конечного поля, то множество неподвижных относительно него элементов тоже образует подполе, которое принято называть неподвижным полем автоморфизма
- произвольный автоморфизм конечного поля, то множество неподвижных относительно него элементов тоже образует подполе, которое принято называть неподвижным полем автоморфизма 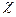 . Таким образом, предыдущее утверждение говорит о том, что неподвижное поле автоморфизма Фробениуса совпадает с простым подполем
. Таким образом, предыдущее утверждение говорит о том, что неподвижное поле автоморфизма Фробениуса совпадает с простым подполем 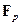 .
.
Кроме того, что поле 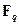 содержит копию
содержит копию 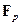 можно добавить, что
можно добавить, что 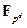 содержит подполе
содержит подполе 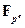 для любого числа
для любого числа  , делящего
, делящего 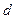 . Это подполе может быть определено как неподвижное поле автоморфизма
. Это подполе может быть определено как неподвижное поле автоморфизма 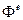 , т. е.
, т. е.
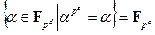 .
.
Другое интересное свойство характеристики  поля
поля 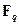 заключается в том, сто взяв произвольный элемент
заключается в том, сто взяв произвольный элемент 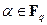 и сложив его с собой
и сложив его с собой  раз, получим ноль. Например, в поле
раз, получим ноль. Например, в поле 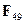 имеет место равенство:
имеет место равенство:
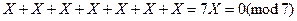 .
.
Ненулевые элементы конечного поля, множество которых обычно обозначают через 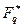 составляют конечную циклическую абелеву группу. Образующая этой группы называется примитивным элементом конечного поля. Примитивный элемент есть в любом конечном поле, поскольку группа его ненулевых элементов всегда циклическая.
составляют конечную циклическую абелеву группу. Образующая этой группы называется примитивным элементом конечного поля. Примитивный элемент есть в любом конечном поле, поскольку группа его ненулевых элементов всегда циклическая.






